15

http://xsy.gdgzez.com.cn/JudgeOnline/problem.php?cid=2354&pid=0

考虑两点 \(x,y\) 在补图上有 \(dis_{x,y}\le 2\)，那么在原图上一定满足 \(\max(deg_x,deg_y)\ge\frac{n}{2}\)。所以以所有满足 \(deg\ge\frac{n}{2}\) 的点为源点都跑一边最短路，这样的点至多只有 \(O(\min(n,\frac{m}{n}))=O(\sqrt m)\) 个，于是复杂度 \(O(m\sqrt m)\)。

如何做到 \(O(m)\) 的补图最短路？在 bfs 时维护还未求出最短路的点集 \(S\)，在将点 \(x\) 出队时，不枚举 \(x\) 的出边，而是枚举 \(S\) 内的点，判断是否与 \(x\) 有连边。容易证明复杂度。

http://xsy.gdgzez.com.cn/JudgeOnline/problem.php?cid=2354&pid=1

诡异的题目。

令 \(sd_x\) 表示 \(x\) 的各位数字和。设 \(dp_{i,j,k}\) 表示数 \(x\) 满足 \(sd_x=i,10^j|x\)，且 \(x\) 的前一个必败点到 \(x\) 的距离为 \(k\) 时，\(x+10^j\) 的前一个必败点到它的距离。从小到大枚举 \(j\)，这是可以转移的。求答案的时候可以一次跳 \(10^j\) 的距离。然后就做完了。

http://xsy.gdgzez.com.cn/JudgeOnline/problem.php?cid=2355&pid=1

考虑怎么做单次。记 \(d\) 是差分数组对 \(m\) 取模后的数组。要选择一个数组 \(d'\)，满足 \(d'_i\bmod m=0\)，最小化 \(\max(\sum\max(d_i-d'_i,0)+\sum\max(d'_i-d_i,0))\)。

结论：\(d'_i=0\) 或 \(d'_i=m\)。这是显然的。

结论：存在 \(0\le x<m\)，使得对于 \(d_i<x,d'_i=0\)；对于 \(d_i\ge x,d'_i=m\)。这是显然的。

枚举这个 \(x\)，然后就可以做单次了。

剩下的数据结构部分是平凡的，对 \(t\) 扫描线即可。

http://xsy.gdgzez.com.cn/JudgeOnline/problem.php?cid=2356&pid=2

好强啊！

先假装 \(n+m\) 为偶数。有一个朴素的 dp 叫做，设 \(dp_{i,j,k}\) 表示确定了最终字符串的前 \(i\) 个和后 \(i\) 个字符，\(s\) 中 \([j,k]\) 这个区间还未匹配的方案数。可以做到 \(O(n^2m)\)，矩乘可以做到 \(O(n^6\log m)\)。

考虑优化这个东西。把转移的 DFA 画出来：

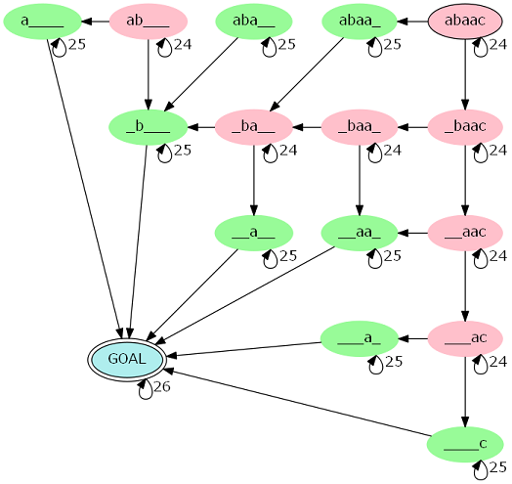
红点表示 \(s_j\not =s_k\)，有一个边权为 \(K-2\) 的自环；绿点表示 \(s_j=s_k\)，有一个边权为 \(K-1\) 的自环。转移边的边权均为 \(1\)。答案就是所有从起点到终点的路径经过的边权之积的和。

注意到其实只关心路径上经过了多少个红点。预处理出 \(f_i\) 表示从起点到终点，经过了 \(i\) 个红点的简单路径的数量。枚举 \(i\)，然后就只要跑一遍状态数为 \(O(n)\) 的矩乘了，复杂度变成了 \(O(n^4\log m)\)。

可以感受到，这个做法对每个 \(i\) 都跑了一遍矩乘，非常的浪费。考虑优化：

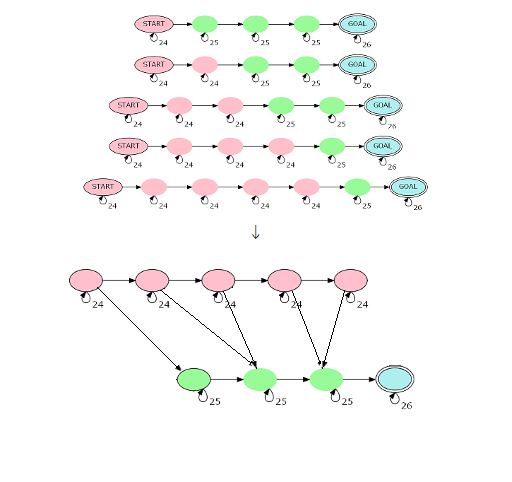
做完了。

如果 \(n+m\) 是奇数怎么办？这相当于钦定了在 DFA 上走的最后一条边不能是同时匹配了两个字符的边，把这个容斥掉，方法和上面是类似的。

然后就真的做完了，复杂度 \(O(n^3\log m)\)。

https://www.luogu.com.cn/problem/AT_wtf22_day2_d

这他妈也太离谱了，这真的是人类能想到的东西吗？

首先钦定每张卡都是不同的，最后除个阶乘。

把恰好 \(k\) 个变成钦定 \(k\) 个，然后二反回去。

那么问题变成，把 \(n\) 张卡分成 \(k\) 组，一组的贡献是 \((sum+cnt)^{\underline{cnt}}\)，求所有方案的贡献之积的和。

接下来要开始骚了！建出一张 \(n^2\) 条边的有向图，\(w_{i,j}=a_j+[j\le i]\)。那么 \((sum+cnt)^{\underline{cnt}}\) 就是，对组里面的每个点都选择一条出边，算所有出边的边权之积的和。这是因为组内排名为 \(i\) 的点的出边边权之和恰好就是 \(sum+i\)。

显然每一组内部都会连出来一个基环树森林。算 \(k\) 个森林的答案不太好搞，变成算 \(k\) 个基环树的方案，然后乘个第二类斯特林数回去。现在问题变成，计算所有包含恰好 \(k\) 个环的连边方式的边权之积的和。

再做个二反变成钦定 \(k\) 个环。

要计算环上的边权之积，看起来我们需要关心环上的点的大小关系，这不好搞了，继续上点手法。把 \(w_{i,j}\) 写成 \(a_j+1-[j>i]\)，然后相当于对环上的每一条边，都可以选择其边权是 \(a_j+1\) 或 \(-[j>i]\)，把所有选择方式的边权之积加起来。

注意到一个环上不可能所有边都选 \(-[j>i]\)，所以如果把选择 \(a_j+1\) 的边拿出来，那环会被断成若干条链，并且每一条链上点的编号都是递增的！所以求出 \(n\) 个点形成了 \(k\) 条链的答案，然后乘个第一类斯特林数回去。

这个可以 dp！设 \(dp_{i,j}\) 表示前 \(i\) 个点形成了 \(j\) 条边的方案数，转移时：

1. 不钦定 \(i\) 在环上，贡献是 \(dp_{i-1,j}\times (sum+i)\)；
2. 把 \(i\) 接在某一条链后面，贡献是 \(-dp_{i-1,j}\times j\)；
3. 新开一条以 \(i\) 为链头的链，贡献是 \(dp_{i-1,j-1}\times (a_i+1)\)。

然后若干反演回去，做完了！时间复杂度 \(O(n^2)\)。

http://xsy.gdgzez.com.cn/JudgeOnline/problem.php?cid=2360&pid=1

考虑一个长这样的东西：

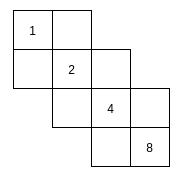
在这个图形的外面再包一层宽度为 \(1\) 的路径，用类似二进制拆分的方法，可以构造出一个合法路径数为 \(k\) 的路径。

但是这样能构造出的 \(k\le 2^{50}\)，过不了。

把上面那个图形改成若干个 \(2\times 3\) 的矩形，相邻两个矩形之间的重叠部分是 \(1\times 2\) 的矩形。这样构造出来的东西就从 \(2\) 的次幂变成了斐波那契数列。经过计算，\(Fib_{100}>>10^{18}\)，于是可以通过。