[BZOJ3280]小R的烦恼

小R的烦恼

题解

此题是一道很明显的网络流，费用流+最大流。

建图其实很好想的，我们可以采取活死人拆点法，将现在活着的人与已死的人拆成两个点，分别是1-n+1与n+2-2(n+1)。每个点表示第i天开始时的活人与死人。在每两天各自的活人与死人之间连一条边，容量为INF，边权为0，因为这一天对第二天能输送的人的值是无限的，有多少都可以送过去。之后，我们在第i天的活人与第i+1天的死人间连一条上下界都为的边，表示这一天肯定要死个人。

接下来就是处理学校的部分，很好写，每所学校就在s与第1天活人间连一条容量为，边权为的边即可。而每座医院就在第天与第天连一条容量为，边权为的边即可。跑一遍EK即可。

问题是我们要如何处理有下界的最大流呢？

我们先来看个例子：（容量上界/下界）

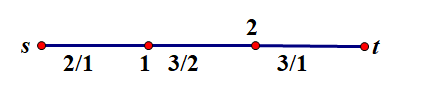
这样的话我们应该怎么处理呢？

我们可以考虑将一条边分离成2条边，一条容量为它的下界，另一条边为它的上界与下界的差，这样连出2m条边。

如图：

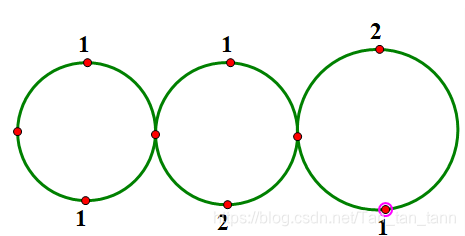
我们将它拆成两条边后，那么就有了一条必要弧与不必要弧，但我们如何才能保证必要弧一定能被走到呢？

我们可以先建一个新原点，将必要弧的u连到y(汇点)，将必要弧的v与x(源点)相连，在原先的源点与汇点间连一条容量为inf的边，这样就可以发现我们是否能将它跑完，如果y的进入流量未满，它就一定不能达到下界。

之后我们再将必要弧拆去，恢复原先的源点与汇点，算出之后的答案，再加上之前的答案即可。

如图：

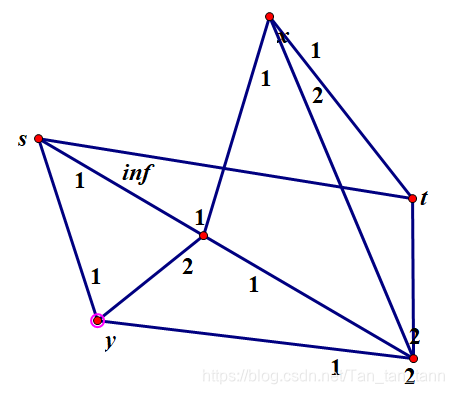
由于此题中上下界相减为0，我们可以不考虑减去后的边，建一次图即可。

源码

#include<cstdio>
#include<cstring>
#include<iostream>
#include<queue>
#define MAXN 100005
#define MAXM 205
using namespace std;
typedef long long LL;
#define int LL
#define gc() getchar()
const int INF=0x7f7f7f7f7f7f;
int tot,head[MAXM],summ;
int from[MAXN],to[MAXN];
int nxt[MAXN],s,t,pre[MAXM];
int dis[MAXM],cap[MAXN],paid[MAXN];
bool vis[MAXM];
int n,m,k;
int a[MAXN],l[MAXN],p[MAXM],d[MAXM],q[MAXM];
template<typename _T>
void read(_T &x){
	_T f=1;x=0;char s=gc();
	while(s>'9'||s<'0'){if(s=='-')f=-1;s=gc();}
	while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=gc();}
	x*=f;
} 
void addEdge(int u,int v,int flow,int cost){
	//printf("%d %d %d %d\n",u,v,flow,cost);
	from[++tot]=u;to[tot]=v;paid[tot]=cost;
	cap[tot]=flow;nxt[tot]=head[u];head[u]=tot;
}
void addedge(int u,int v,int flow,int cost){
	//printf("%d %d %d %d\n",u,v,flow,cost);
	addEdge(u,v,flow,cost);addEdge(v,u,0,-cost);
}
int EK(){
	int res=0,sum=0;bool fg=false;
	while(1){
		for(int i=0;i<=t;i++) dis[i]=INF,vis[i]=0,pre[i]=-1; 
		queue<int> q;while(!q.empty()) q.pop();
		dis[s]=0;vis[s]=1;q.push(s);
		while(!q.empty()){
			int now=q.front();q.pop();vis[now]=0;
			for(int i=head[now];~i;i=nxt[i]){
				int v=to[i];//printf("%d %d %d %d %d\n",now,v,dis[now],paid[i],dis[v]);
				if(cap[i]>0&&dis[v]>dis[now]+paid[i]){
					dis[v]=dis[now]+paid[i];pre[v]=i;
					if(!vis[v]) q.push(v),vis[v]=1;
				}
			}
		}
		//printf("dis%d %d\n",res,dis[t]);
		if(dis[t]>INF-1||dis[t]+res<0)return summ==sum?res:-1;int minn=INF;
		for(int i=pre[t];~i;i=pre[from[i]])minn=min(minn,cap[i]);
		for(int i=pre[t];~i;i=pre[from[i]])cap[i]-=minn,cap[i^1]+=minn;
		res+=dis[t]*minn;sum+=minn;fg=true;
		//printf("%d %d %d\n",res,minn,dis[t]);
	}
}
signed main() {
	int tt,ttott=0;read(tt);
	while(tt--){
		tot=-1;memset(head,-1,sizeof(head));
		read(n);read(m);read(k);n++;
		s=0;t=2*n+1;
		for(int i=1;i<n;i++) read(a[i]);
		for(int i=1;i<=m;i++) read(l[i]),read(p[i]);
		for(int i=1;i<=k;i++) read(d[i]),read(q[i]);
		for(int i=1;i<n;i++) addedge(i,i+1,INF,0),addedge(i+n,i+n+1,INF,0);
		for(int i=1;i<=k;i++)
			for(int j=2;j<=n-d[i];j++)
				addedge(j+n,j+d[i],a[j+d[i]],q[i]);
		for(int i=1;i<=m;i++) addedge(s,1,l[i],p[i]);
		addedge(2*n,t,INF,0);addedge(t,s,INF,0);
		s=2*n+2;t=2*n+3;summ=0;
		for(int i=1;i<n;i++)
			addedge(i,t,a[i],0),addedge(s,i+n+1,a[i],0),summ+=a[i];
		int tmp=EK();
		if(tmp>0) printf("Case %lld: %lld\n",++ttott,tmp); 
		else printf("Case %lld: impossible\n",++ttott);
	}
    return 0;
}

谢谢！！！