楼房搭建
楼房搭建

题解
做法挺奇特的,可能是笔者做题做少了
首先,简单的dp暴力还是挺好想的。
就直接定义
f
i
,
j
f_{i,j}
fi,j表示第
i
i
i个建筑为
j
j
j且前
i
−
1
i-1
i−1个建筑均满足条件的最小所需时间。
转移方程式
f
i
,
2
b
+
a
=
min
(
g
i
−
1
,
h
i
−
1
−
2
a
−
b
+
a
+
b
)
f_{i,2b+a}=\min(g_{i-1,h_{i-1}-2a-b}+a+b)
fi,2b+a=min(gi−1,hi−1−2a−b+a+b),其中
g
g
g表示后缀最大值。
时间复杂度
O
(
n
3
)
O\left(n^3\right)
O(n3),只能拿50pts。
但我们发现
2
b
+
a
2b+a
2b+a可以与
2
a
+
b
2a+b
2a+b合并,得到
3
a
+
3
b
3a+3b
3a+3b,转移式可以改改,有
f
i
,
j
=
min
(
f
i
−
1
,
k
+
j
+
k
3
)
[
j
2
⩽
k
⩽
2
j
]
f_{i,j}=\min(f_{i-1,k}+\frac{j+k}{3})[\frac{j}{2}\leqslant k\leqslant 2j]
fi,j=min(fi−1,k+3j+k)[2j⩽k⩽2j]
再改改,
f
i
,
j
=
min
(
f
i
−
1
,
k
+
k
3
)
+
j
3
[
j
2
⩽
k
⩽
2
j
]
f_{i,j}=\min(f_{i-1,k}+\frac{k}{3})+\frac{j}{3}[\frac{j}{2}\leqslant k\leqslant2j]
fi,j=min(fi−1,k+3k)+3j[2j⩽k⩽2j]
这样我们只需要保证
j
+
k
j+k
j+k的和是3的倍数即可,可以将
f
i
−
1
f_{i-1}
fi−1建出线段树,再去查
[
j
2
,
2
j
]
[\frac{j}{2},2j]
[2j,2j]中最大的
f
i
−
1
,
k
+
k
3
f_{i-1,k}+\frac{k}{3}
fi−1,k+3k即可。
时间复杂度
O
(
n
2
l
o
g
n
)
O\left(n^2log\,n\right)
O(n2logn),能拿到70pts。
但现在还是跟
n
⩽
1
0
6
n\leqslant 10^6
n⩽106有很大的差距,得考虑一些很新奇的做法。
其实我们发现,我们没必要将每个建筑当前的高度保留下来,反正它一定会达到它需要的高度。
而所有的高度都可以转化为连续的3加上一个(1,2)或(2,1)或不加。同时所有的增加的方法也可以进行转化。
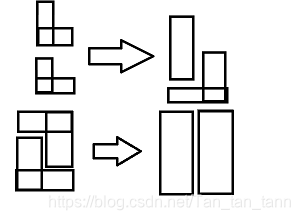
由此,所有的操作都可以向这样进行转换。
很容易发现,将这个点刚好用一堆3和一个(2,1)或(1,2)或没有的方法凑满后再用这个点凑得的方法去更新下一个点一定是最优的,这样可以保证下一个点所需的更新次数最小。
(下面将在这列加上3的操作成为更新3,更新1与更新2同理)
关键是下一个点能直接更新的代价为1的3有多少。
很明显,是上一个节点更新的用代价1更新3的数量的两倍加上更新2的数量。
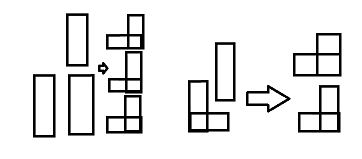
即使你这个节点的更新3是通过上一个节点的更新2和3得到的,也可以反悔成这个样子。
可以自己尝试画一下,这里就不画了。虽说只是因为笔者太懒了
由于更新3的使用是有前一个点限制的,除去这样的更新3,剩下就只能通过更新1与更新2来补全。
容易发现,即使是补全的时候也是能用更新2就用更新2,因为更新2能给下一个点提供更多的更新3使用机会,用更新1反而会导致下一个点超过需求的可能性更大,也就是浪费更多。
将下一个点减去这个点更新1与更新2对其产生的贡献后,就可以这样依次更新下去就可以了。
答案就是所有的更新次数和。
时间复杂度 O ( n ) O\left(n\right) O(n)。
源码
#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
#define MAXN 1000005
typedef long long LL;
const LL INF=0x7f7f7f7f7f7f;
template<typename _T>
void read(_T &x){
_T f=1;x=0;char s=getchar();
while('0'>s||s>'9'){if(s=='-')f=-1;s=getchar();}
while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
x*=f;
}
LL n,h[MAXN],ti[MAXN],ans;
int main(){
freopen("building.in","r",stdin);
freopen("building.out","w",stdout);
read(n);for(int i=1;i<=n;i++)read(h[i]);LL t1,t2,t3;
for(int i=1;i<=n;i++){
t3=min(h[i]/3LL,ti[i]);h[i]-=3LL*t3;t2=h[i]/2LL;h[i]-=2LL*t2;t1=h[i];
h[i+1]=max(0LL,h[i+1]-t2-2LL*t1);ti[i+1]=2LL*t3+t2;ans+=t3+t2+t1;
}
printf("%lld\n",ans);
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号