[海军国际项目办公室]矩阵
矩阵
总所周知, N O I P = N I P O = N a v a l I n t e r n a t i o n a l P r o g r a m O f f i c e NOIP=NIPO=Naval\,International\,Program\,Office NOIP=NIPO=NavalInternationalProgramOffice,所以我们就把NOIP模拟赛的习题叫做海军国际项目办公室吧。
题解
我们考虑将原矩阵转化成一个序列,计算这个序列的个数。
对于一个大小为 n × n n\times n n×n的矩阵,它上面总共有 2 n 2n 2n个黑点。我们记第 i i i列的两个黑点的行号为 a i , 0 , a i , 1 a_{i,0},a_{i,1} ai,0,ai,1,我们的序列可以表示为 { a 1 , 0 , a 1 , 1 , a 2 , 0 , a 2 , 1 , . . . , a n , 0 , a n , 1 } \{a_{1,0},a_{1,1},a_{2,0},a_{2,1},...,a_{n,0},a_{n,1}\} {a1,0,a1,1,a2,0,a2,1,...,an,0,an,1}。
我们记序列中第 i i i个数为 b i b_{i} bi,原序列为 B B B。
由于每一行有且仅有两个数,所以 [ 1 , n ] [1,n] [1,n]中每个数在原序列中出现刚好两次。
而且同一列中不可能两个黑点的位置都相同,所以 b 2 k + 1 ≠ b 2 k + 2 ( k ∈ [ 0 , n − 1 ] ∩ N ) b_{2k+1}\not =b_{2k+2}(k\in [0,n-1]\cap N) b2k+1=b2k+2(k∈[0,n−1]∩N)。
但如果直接去求这样的序列的转移方法的话无疑是非常复杂的,我们考虑先将不同数之间的顺序去掉,只看这两个数相同或者不同。
我们可以将相同的两个数之间连边,也就得到一个这样的序列:
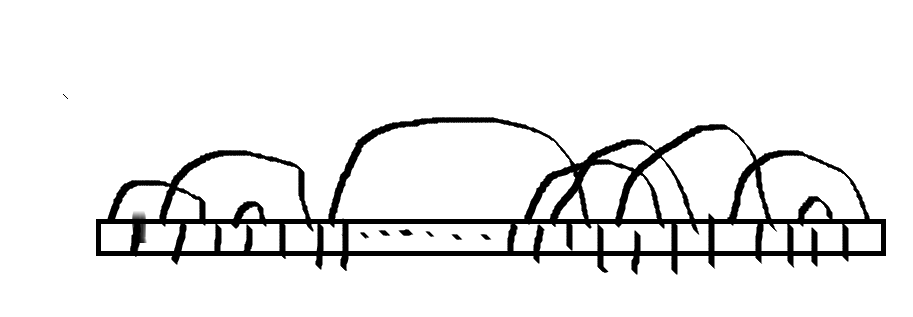
我们要保证的条件是一条线段的起终点不能同时是 2 k + 1 , 2 k + 2 ( k ∈ [ 0 , n − 1 ] ∩ N ) 2k+1,2k+2(k\in [0,n-1]\cap N) 2k+1,2k+2(k∈[0,n−1]∩N)。
我们设长度为 2 i 2i 2i的合法序列有 d p i dp_{i} dpi个,考虑 d p i dp_{i} dpi可以如何转移。
假设我们已经有了一个长度为 2 ( n − 1 ) 2(n-1) 2(n−1)的序列,现在又加上两个位置。
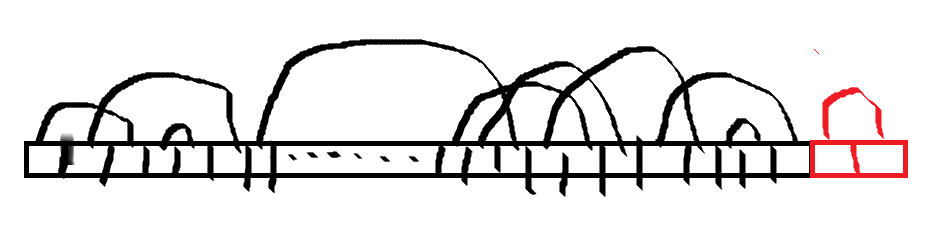
我们现在可以将其中一个位置与前面任意的一个位置替换,得到一个新序列。
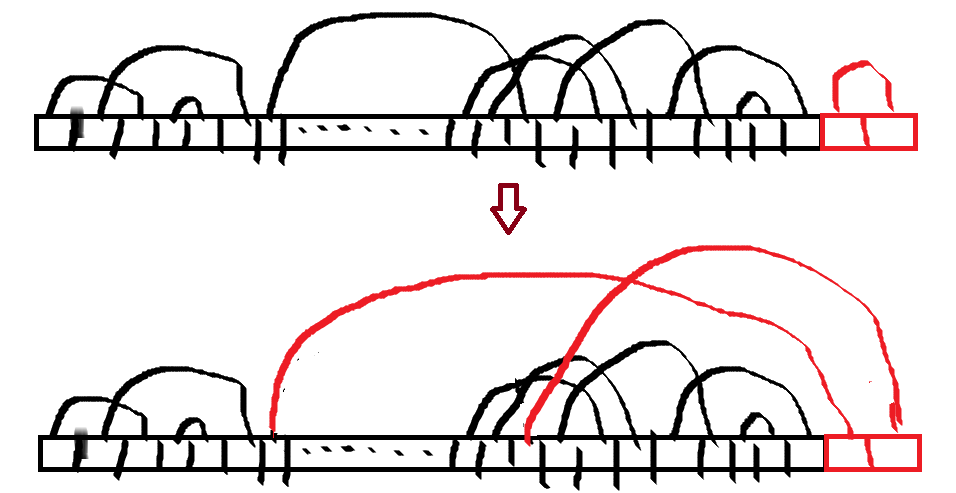
可以理解成已有点对 ( u , v ) , ( 2 n − 1 , 2 n ) (u,v),(2n-1,2n) (u,v),(2n−1,2n)转化成 ( u , 2 n − 1 ) ( v , 2 n ) (u,2n-1)(v,2n) (u,2n−1)(v,2n)或 ( u , 2 n ) ( v , 2 n − 1 ) (u,2n)(v,2n-1) (u,2n)(v,2n−1)。
由于之前已经有 d p i − 1 dp_{i-1} dpi−1个不同的合法序列,每个序列中含有 i − 1 i-1 i−1个点对,转化后的序列又都是不同的,所以 d p i + = 2 ( i − 1 ) d p i − 1 dp_{i}+=2(i-1)dp_{i-1} dpi+=2(i−1)dpi−1。
但这并不是完全的 然而笔者考场上并没有看出来 ,这样转化后形成的新点对
(
u
,
2
n
−
1
)
(u,2n-1)
(u,2n−1)与
(
v
,
2
n
)
(v,2n)
(v,2n)的起点
u
,
v
u,v
u,v不能在
2
k
+
1
,
2
k
+
2
(
k
∈
[
0
,
n
−
1
]
∩
N
)
2k+1,2k+2(k\in [0,n-1]\cap N)
2k+1,2k+2(k∈[0,n−1]∩N)的位置上,所以我们还要有另一部分的转移。
我们将相邻的两个位置看成一个块,很明显,我们将这样的序列中 ( u , v ) , ( 2 n − 1 , 2 n ) (u,v),(2n-1,2n) (u,v),(2n−1,2n)这两个块去掉后得到的长度为 2 n − 4 2n-4 2n−4的序列仍然是一个合法的序列。
这样的话, ( 2 n , 2 n + 1 ) (2n,2n+1) (2n,2n+1)所属位置是固定的, ( u , v ) (u,v) (u,v)所属的块有 n − 1 n-1 n−1种可能。
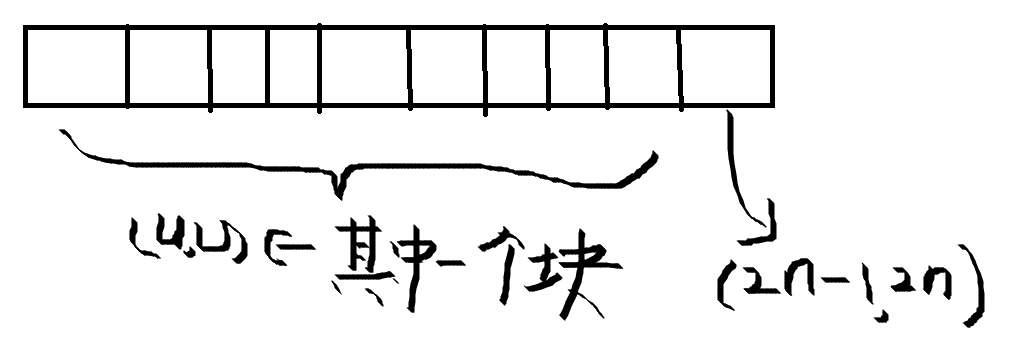
而 ( u , v ) (u,v) (u,v)与 ( 2 n , 2 n + 1 ) (2n,2n+1) (2n,2n+1)两个块之间的连接方式又有两种:
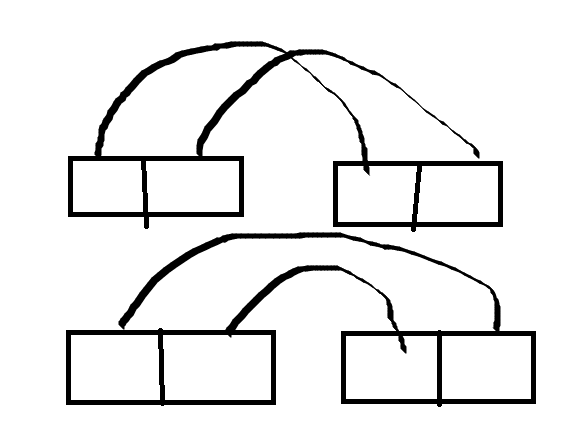
所以也有 d p i + = 2 ( i − 1 ) d p i − 2 dp_{i}+=2(i-1)dp_{i-2} dpi+=2(i−1)dpi−2。
可以得出总的转移式,
d
p
i
=
2
(
i
−
1
)
(
d
p
i
−
1
+
d
p
i
−
2
)
dp_{i}=2(i-1)(dp_{i-1}+dp_{i-2})
dpi=2(i−1)(dpi−1+dpi−2)
其实我们也可以反过来想,对于最后一个块,它的两个起点是连在前面的。我们将最后一个块的两个点去掉,将其前面对应的两个点相连。
它既有可能得到一个长度为 2 ( n − 1 ) 2(n-1) 2(n−1)的合法序列,也可能得到一个长度为 2 ( n − 1 ) 2(n-1) 2(n−1)的非法序列。这个非法序列如果去掉那个非法的块就是一个长度为 2 ( n − 2 ) 2(n-2) 2(n−2)的合法序列了。而那两个点无论去掉后是否合法都有 2 ( n − 1 ) 2(n-1) 2(n−1)种练法,所以是 2 ( i − 1 ) ( d p i − 1 + d p i − 2 ) 2(i-1)(dp_{i-1}+dp_{i-2}) 2(i−1)(dpi−1+dpi−2)。
你甚至可以放到树上去想,每次操作就相当于给某个点多一个儿子,或加上一个大小为二的树,加上的树插回原值种也有 ( n − 1 ) (n-1) (n−1)种。
由于我们上面的序列的构造并没有考虑不同环之间,所以我们的答案还需乘上 n ! n! n!。
同时同一列中两个位置是没有关系的,也就是说序列中无论两个块是 a i , 0 > a i , 1 a_{i,0}>a_{i,1} ai,0>ai,1还是 a i , 1 > a i , 0 a_{i,1}>a_{i,0} ai,1>ai,0都是一样的,所以还得乘上 2 − n 2^{-n} 2−n。
于是,有:
A
n
s
=
∑
i
=
1
n
f
(
i
)
=
∑
i
=
1
n
i
!
2
i
d
p
i
Ans=\sum_{i=1}^{n}f(i)=\sum_{i=1}^{n}\frac{i!}{2^i}dp_{i}
Ans=i=1∑nf(i)=i=1∑n2ii!dpi
其实我们上面的序列的构造是早有先例的。
有著名的舞蹈问题: 2 n 2n 2n个人要与配偶以外的任何性别的伴侣匹配的方法数。 2 n 2n 2n个人最初以某种方式配对,然后重新配对,以便没有对象与其原始伙伴。
a 0 = 1 , a 1 = 0 , a i = 2 ( i − 1 ) ( a i − 1 + a i − 2 ) a_{0}=1,a_{1}=0,a_{i}=2(i-1)(a_{i-1}+a_{i-2}) a0=1,a1=0,ai=2(i−1)(ai−1+ai−2)E G F : 1 e x p ( x ) 1 − 2 x EGF:\frac{1}{exp(x)\sqrt{1-2x}} EGF:exp(x)1−2x1
a ( n ) = ( − 1 ) n ∑ k = 0 n ( − 1 ) k ( n k ) ( 2 k − 1 ) ! ! a(n)=(-1)^n\sum_{k=0}^{n}(-1)^k\binom{n}{k}(2k-1)!! a(n)=(−1)nk=0∑n(−1)k(kn)(2k−1)!!
所以我们只需要用以上的 d p dp dp式将 d p 0... n dp_{0...n} dp0...n都求出来,算出答案即可。
时间复杂度 O ( n ) O\left(n\right) O(n)。
源码
int n,fac[MAXN],dp[MAXN],iv2[MAXN],ans;
signed main(){
freopen("matrix.in","r",stdin);
freopen("matrix.out","w",stdout);
read(n);dp[2]=2;dp[3]=8;dp[4]=60;
fac[0]=fac[1]=iv2[0]=1;iv2[1]=inv2;
for(int i=2;i<=n;i++)fac[i]=1ll*i*fac[i-1]%mo,iv2[i]=1ll*iv2[i-1]*inv2%mo;
for(int i=5;i<=n;i++)dp[i]=2ll*(i-1)*add(dp[i-1],dp[i-2])%mo;
for(int i=1;i<=n;i++)printf("%d:%d\n",i,dp[i]);
for(int i=2;i<=n;i++)ans=add(ans,1ll*dp[i]*iv2[i]%mo*fac[i]%mo);
printf("%d\n",ans);
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号