[海军国际项目办公室]简单题

简单题

题面

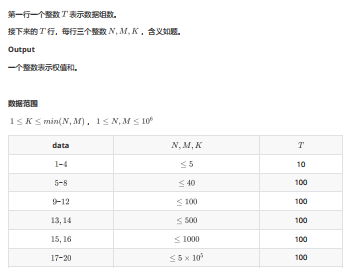
题解

一般取这种标题的都不是什么好题。

看到这种题，我们首先很容易考虑到$dp$。
我们定义$d{p}_{i,j,k}$表示选了$i$个数，$a$的和为$j$，$b$的和为$k$时的答案。
容易得到递推式:
$$d{p}_{i,j,k}=\sum _{x=1}^j\sum _{y=1}^k\min (x,y)d{p}_{i-1,j-x,k-y}$$
很明显直接这样做是$O\left(Tk{n}^2{m}^2\right)$，大概可以拿$20pts$。
但事实上上面的式子的系数至于$x,y$中较小的一个有关，我们可以尝试枚举$x$或$y$中某一个作为较小的一个，通过前锥和转移。
这样做的话是$O\left(Tknm(n+m)\right)$的，可以拿到$40pts$。
但我们很容易发现，前面的系数是针对$j,k$这两维的，这两维从某种形式上说是等价的。
所以$d{p}_{i-1,j^{\prime },k^{\prime }}$对$d{p}_{i,j,k}$的贡献实际上是$\min (j-j^{\prime },k-k^{\prime })$，我们可以考虑通过差分的形式来维护。
$d{p}_{i-1,j^{\prime },k^{\prime }}$对$d{p}_{i,j,k}$的贡献的系数是等价于函数$\{\begin{array}{c}x=j^{\prime }+\Delta \\ y=k^{\prime }+\Delta \end{array}(\Delta >0)$在$(0,0)$与$(j,k)$构成的矩形中所经过的整点数。
同样，一次转移中，$d{p}_{i,j,k}$处相较于它前面的点新增的贡献就是从它往斜上方走的那条斜线上的点的$dp$值之和，我们可以对于每个点都记录下他的新增转移。
点$j,k$处新增转移我们记作$di{f}_{i,j,k}$，很明显有
$$di{f}_{i,j,k}=di{f}_{i,j-1,k-1}+d{p}_{i-1,j-1,k-1}$$
故，$dp$值的转移等价于
$$d{p}_{i,j,k}=d{p}_{i,j-1,k}+\sum _{l=1}^{k}di{f}_{i,j,l}$$
后面的部分可以用前缀和进行优化，这样，我们的时间复杂度就是$O\left(Tknm\right)$了。
虽然我们不可能将大小为$500\times 500\times 500$的$dp$数组都记录下来，但我们完全可以先将询问离线，对于每个$k$得到$d{p}_{k,i,j}$时记录$k$值为这个询问的答案即可。
这样，我们就可以将$T$去掉了，时间复杂度$O\left(knm+T\right)$，有$70pts$。

我们的$dp$貌似已经无法继续优化了，考虑用其它方法求我们的答案，恰好上面的式子很适合我们使用多项式。
我们记二元生成函数$f_i(j,k)$表示$d{p}_{i,j,k}$的值，由于我们$f_i$转移到$f_{i+1}$每次都是加入一个数，我们沿用上面的转移式子：
$$f_0=1,f_i=f_{i-1}\cdot g=g^i$$
可以得到多项式$g$的表达式，
$$g=\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }\min (i,j)x^i{y}^j=\sum _{k=1}^{\infty }\sum _{i=k}^{\infty }\sum _{j=k}^{\infty }{x}^i{y}^j=\sum _{k=1}^{\infty }(\sum _{i=k}^{\infty }{x}^i)\cdot (\sum _{j=k}^{\infty }{y}^j)$$
代入总所周知的式子${\sum }_{i=0}^{\infty }{x}^i=\frac{1}{1-x}$，可得，
$$g=\sum _{k=1}^{\infty }\frac{x^k}{1-x}\cdot \frac{y^k}{1-y}=\frac{{\sum }_{k=1}^{\infty }{x}^k{y}^k}{(1-x)(1-y)}=\frac{\frac{xy}{1-xy}}{(1-x)(1-y)}=\frac{xy}{(1-x)(1-y)(1-xy)}$$
得到上面这个式子，如果我们用二元函数的卷积展开去做(就是将转化成$n$进制的数去做一次函数的卷积)，时间复杂度是$O\left(nm\log k\log nm\right)$的，大概可以过掉$80pts$。
然而实际上我们的$C2020jzm$(其真实实力的颜色)巨佬(即OneInDark巨佬)还推出了一个奇怪的式子，$dp$得到了$80pts$。
但是我们明显还有更简洁的方法去做，将上面的式子回代，
$$g=\frac{xy}{1-xy}\cdot \frac{1}{1-x}\cdot \frac{1}{1-y}=(\sum _{i=1}^{\infty }{x}^i{y}^i)(\sum _{i=1}^{\infty }{x}^i)(\sum _{i=1}^{\infty }{y}^i)$$
我们的答案，
$$f_k(n,m)=[x^n{y}^m]g^k=[x^n{y}^m](\sum _{i=1}^{\infty }{x}^i{y}^i{)}^k(\sum _{i=0}^{\infty }{x}^i{)}^k(\sum _{i=0}^{\infty }{y}^i{)}^k$$
上面的式子明显可以用组合求出答案，我们可以枚举第一个$({\sum }_{i=1}^{\infty }{x}^i{y}^i{)}^k$对我们的次数产生的贡献，显然有，
$$f_k(n,m)=\sum _{i=k}^{\min (n,m)}\left(\genfrac{}{}{0ex}{}{i-1}{k-1}\right)\left(\genfrac{}{}{0ex}{}{n-i+k-1}{k-1}\right)\left(\genfrac{}{}{0ex}{}{m-i+k-1}{k-1}\right)$$
这样，对于单个询问，我们的时间复杂度就是$O\left(\min (n,m)-k\right)$的了。

总时间复杂度$O\left(Tn\right)$。

源码

#include<bits/stdc++.h>
using namespace std;
#define MAXN 1000005
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
typedef long long LL;
typedef unsigned long long uLL;
const LL INF=0x3f3f3f3f3f3f3f3f;
const int mo=998244353;
const int inv2=499122177;
const int jzm=2333;
const int zero=10000;
const int orG=3,invG=332748118;
const double Pi=acos(-1.0);
const double eps=1e-5;
typedef pair<int,int> pii;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){
	_T f=1;x=0;char s=getchar();
	while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}
	while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
	x*=f;
}
template<typename _T>
void print(_T x){if(x<0){x=(~x)+1;putchar('-');}if(x>9)print(x/10);putchar(x%10+'0');}
LL gcd(LL a,LL b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1LL)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1LL;}return t;}
int T,n,m,k,fac[MAXN],inv[MAXN],f[MAXN],ans;
void init(){
	fac[0]=fac[1]=inv[0]=inv[1]=f[1]=1;
	for(int i=2;i<=1e6;i++){
		fac[i]=1ll*i*fac[i-1]%mo;
		f[i]=1ll*(mo-mo/i)*f[mo%i]%mo;
		inv[i]=1ll*inv[i-1]*f[i]%mo;
	}
}
int C(int x,int y){
	if(x<0||y<0||x<y)return 0;
	return 1ll*fac[x]*inv[y]%mo*inv[x-y]%mo;
}
signed main(){
	//freopen("easy.in","r",stdin);
	//freopen("easy.out","w",stdout);
	init();read(T);
	while(T--){
		read(n);read(m);read(k);ans=0;
		for(int i=k;i<=min(n,m);i++)
			ans=add(ans,1ll*C(i-1,k-1)*C(n-i+k-1,k-1)%mo*C(m-i+k-1,k-1)%mo,mo);
		printf("%d\n",ans);
	}
	return 0;
}

谢谢！！！