[海军国际项目办公室]快递

快递

题面

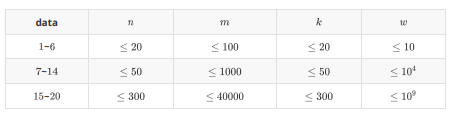
题解

首先当我们看到$n,k⩽300$的数据范围与按顺序执行订单的要求，我们很容易联想到通过动态规划来解决我们遇到的问题。
先定义$d{p}_{i,j,k,l}$表示我们已经完成了$i$个任务，设立的两个传送门分别在位置$j,k$，我们当前所在点为$l$的最少花费时间。
由于我们得保证花费时间是最少的，所以我们实际上的转移式比较类似于$Dijk$的最短路，需要拿优先队列来维护，时间复杂度$O\left(k{n}^2(n+m)log(n+m)\right)$。

但事实上我们发现我们没必要记录下我们具体在哪个位置，中间路程我们没必要一步一步地走过去，我们的每条路线的出发点于终点是固定的，都是以下的形式，
$$1->a_1->b_1->a_2->b_2->a_3->...->b_k$$
这样，我们可以将我们所有的任务转化成在两个点之间的移动。我们完成任务时就在其中的一个节点上，我们不在节点上时只是在去节点/传送门的路上。
所以我们真正的状态只需要记录下它当前的位置是在任务完成位置还是传送门的位置，一次$dp$的转移我们可能的方向只有两种，到达下一个目标点或者在某个位置新建传送门。
至于到这个点的距离，我们可以一开始就用$Floyed$处理出来。
现在我们的时间复杂度是$O\left(k{n}^{3}logn\right)$，事实上并没有优化多少，大概有$70pts$的样子，考虑优化。

该怎么优化呢？转移明显是不大能优化的，我们只能从原来的$dp$状态上入手。
这时，我们就只能发挥我们强大的第六感以及 幸运$EX$ 去猜结论了，我们可以猜测：

• 任何时刻实际上真正有用的传送门只有一个，另一个传送门可以随便丢掉

这样刚好可以让我们的状态数少掉一个$n$，轻松通过此题。
其实想到这里也很好感性证明了。
如果我们有两个传送门，在之后都会使用，我们不妨设其分别为$u,v$，我们的路径可能是这样的，
$$a_i->u->v->a_{i+1}->v->u->a_{i+1}$$
它是最优秀的，但我们明显可以构造出一个与它一样优秀的方法，我们开始时用$a_i$替换掉$u$，那我们的路径变为，
$$a_i->v->a_{i+1}->v->a_i->a_{i+1}$$
很明显，$a_i->u->a_{i+1}$的距离是不小于$a_i->a_{i+1}$的距离的，这种做法只有可能更优。
因为我们无论如何都会需要$a_i->u$这段的距离，但这段在前面走还是在后面走走都是一样的，后面甚至可以不在这条路。
还有可能会有这样的情况，
$$a_i->u->v->a_{i+1}->a_{i+2}->...->a_j->u->v->a_{j+1}$$
相当于我们绕了一圈回来，这种情况下我们相当于之前一直固定有效传送门$v$，绕回来时在$u$点设定传送门再传送到$v$，这同样是可行的。
事实上，无论何时，我们真正有效的传送门都只有一个，所以在我们的$dp$状态中只需要保存一个传送门。
这样我们的转移还是有两种，找新传送门/转移到下一个任务。注意再转移到下一个任务时如果使用传送门你会在原地加传送门再过去，这时我们需要注意保留下来的传送门是哪一个。
这样，我们整个$dp$转移过程是$O\left(k{n}^{2}logn\right)$。

事实上我们同时可以发现，无论如何，我们在从一个目标点到另一个目标点时，我们最多只会改变一次有效传送门，所以每次转移我们的完成任务数都是$+1$的。
故我们可以直接$dp$，没必要通过优先队列来维护转移。

总时间复杂度$O\left(k{n}^2\right)$，然而笔者写的是$O\left(k{n}^{2}logn\right)$，也过了。

源码

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
typedef long long LL;
typedef unsigned long long uLL;       
const LL INF=0x3f3f3f3f3f3f3f3f;       
const int mo=998244353;
const int inv2=499122177;
const int jzm=2333;
const int zero=10000;
const int orG=3,invG=332748118;
const double Pi=acos(-1.0);
const double eps=1e-5;
typedef pair<int,int> pii;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){
	_T f=1;x=0;char s=getchar();
	while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}
	while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
	x*=f;
}
template<typename _T>
void print(_T x){if(x<0){x=(~x)+1;putchar('-');}if(x>9)print(x/10);putchar(x%10+'0');}
LL gcd(LL a,LL b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1LL)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1LL;}return t;}
int n,m,k,d[605],totd;
LL mp[305][305],dp[605][305][2];
struct ming{
	int tk,x,typ;LL dp;
	bool friend operator < (const ming &x,const ming &y){
		return x.dp>y.dp;
	}
};
priority_queue<ming>q;
signed main(){
	//freopen("express.in","r",stdin);
	//freopen("express.out","w",stdout);
	memset(mp,0x3f,sizeof(mp));read(n);read(m);read(k);
	for(int i=1;i<=m;i++){
		int u,v;LL w;read(u);read(v);read(w);
		mp[u][v]=mp[v][u]=min(mp[u][v],w);
	}
	for(int i=1;i<=n;i++)mp[i][i]=0;
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				mp[i][j]=min(mp[i][j],mp[i][k]+mp[k][j]);
	d[0]=1;
	for(int i=1;i<=k;i++){
		int a,b;read(a);read(b);
		d[++totd]=a;d[++totd]=b;
	}
	memset(dp,0x3f,sizeof(dp));
	dp[0][0][0]=0;q.push((ming){0,0,0,0LL});
	while(!q.empty()){
		ming t=q.top();q.pop();int id=t.tk,u;
		if(dp[id][t.x][t.typ]!=t.dp)continue;
		if(id==totd){printf("%lld\n",dp[id][t.x][t.typ]);return 0;}
		if(t.typ==0)u=d[id];else u=t.x;
		LL tmp=min(mp[u][d[id+1]],mp[t.x][d[id+1]]);
		if(t.dp+tmp<dp[id+1][t.x][0]){
			dp[id+1][t.x][0]=t.dp+tmp;
			q.push((ming){id+1,t.x,0,dp[id+1][t.x][0]});
		}
		if(t.dp+tmp<dp[id+1][u][0]){
			dp[id+1][u][0]=t.dp+tmp;
			q.push((ming){id+1,u,0,dp[id+1][u][0]});
		}
		for(int i=1;i<=n;i++){
			if(i==t.x)continue;tmp=min(mp[u][i],mp[t.x][i]);
			if(dp[id][i][1]>t.dp+tmp){
				dp[id][i][1]=t.dp+tmp;
				q.push((ming){id,i,1,dp[id][i][1]});
			}
		}
	}
	return 0;
}

谢谢！！！