[硫化铂]二十

二十

题目概述

题解

首先，对于原来的这个我们要求的这个期望卡壳距离，我们显然可以用积分来解决。
显然，我们一次卡壳会对应某一个对于当前斜率的最大点与最小点，它们间的距离就是本次卡壳的距离。我们把它拆成两个方向的向量，显然靠下的一个向量对应的是减，靠上的对应的是加，它们方向是不同的。
我们要算的也就是任意一个方向的向量对应的最远/近的点，那么有式子，
$$Ans={\int }_0^{2\pi }\sqrt{x^{\prime }(\theta {)}^2+y^{\prime }(\theta {)}^2}d\theta$$这不就是周长吗？具体怎么积的就不写了 ，因为我也不会。
实际上也可以感性理解一下，我们的期望的距离就是直径，乘上$\pi$也就化作一个圆，这个期望的圆的周长应该是等价于我们的我们原图形的周长，因为是期望将原图变形过来的嘛。

好的，我们现在的重点就是该怎么算这个周长。
算周长的第一步显然是得先将这凸包上有哪些点算出来，由于这个凸包的许多边角地区都是圆上的部分不妨直接记录下来有哪些圆，与这个圆对应的$\theta$区间。
显然，这些$\theta$区间都是不重叠的，而且端点数量不会特别多，因为一个圆相对于另一个圆最优的一定是一段连续区间，每次就覆盖一个区间上去，最后得到的自然是线性级别的区间，这个证明与某队爷的虚构推理的证明有点像。话说这道题我现在还没过。
那么我们就可以采用归并的方法求出我们最后的凸包。
分治每个点流维护$[0,2\pi ]$中所有对应同一个圆的角度区间的连续段，合并覆盖同一个角度段的圆时，我们可以算出两个圆互相的优劣关系，从而拆开这个区间。
显然，两个圆各自的最优区间合起来是一个环上的两端，也就是说有两个端点。
显然，这两个端点都是这两个圆的同侧公切线，我们要算的就是这两个圆的公切线。
学过高中解析几何的人应该都会，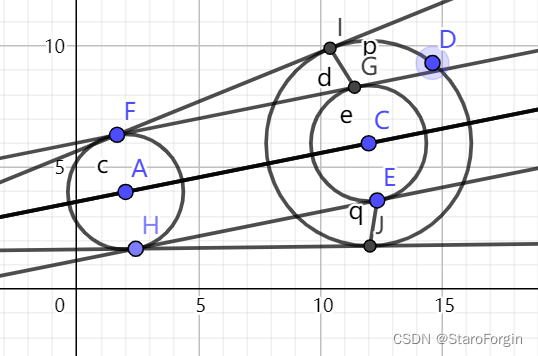
画得不是很好，见谅。
我们不妨把$\angle FIG$与$\angle HJE$看成直角，在较大圆内部做一个与较小圆相等的圆。
显然，$AC//FG//HE$，而且$IG$与$EJ$又是两圆半径的差，那么我们自然而然就可以轻松的推到$FI$与$HJ$的角度了。
就这样就可以轻松的划分我们的区间了。
归并完后简单地就可以算出答案。
注意，归并不同角度区间时相邻的区间如果是同一个圆是要合并的，不然不能保证总圆个数的线性。或许也可以?

时间复杂度$O\left(n\log n\right)$。

源码

#include<bits/stdc++.h>
using namespace std;
#define MAXN 500005
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
#define lson (rt<<1)
#define rson (rt<<1|1)
typedef long long LL;
typedef unsigned long long uLL; 
typedef long double ld;
typedef pair<double,double> pii;
const int INF=0x3f3f3f3f;
const int mo=1e9+7;
const int mod=1e5+3;
const int inv2=499122177;
const int jzm=2333;
const int zero=2000;
const int n1=2000;
const int orG=3,ivG=332748118;
const double Pi=acos(-1.0);
const double eps=1e-8;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){
	_T f=1;x=0;char s=getchar();
	while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}
	while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
	x*=f;
}
template<typename _T>
void print(_T x){if(x<0){x=(~x)+1;putchar('-');}if(x>9)print(x/10);putchar(x%10+'0');}
int gcd(int a,int b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*t*a%p;a=1ll*a*a%p;s>>=1;}return t;}
double sqr(double x){return x*x;}
struct point{
	double x,y;point(){x=y=0;}
	point(double X,double Y){x=X;y=Y;}
	point operator + (const point &rhs)const{return point(x+rhs.x,y+rhs.y);}
	point operator - (const point &rhs)const{return point(x-rhs.x,y-rhs.y);}
	double operator * (const point &rhs)const{return x*rhs.x+y*rhs.y;}
	double operator ^ (const point &rhs)const{return x*rhs.y-y*rhs.x;}
	point operator * (const double &rhs)const{return point(x*rhs,y*rhs);}
	point operator / (const double &rhs)const{return point(x/rhs,y/rhs);}
	bool operator == (const point &rhs)const{return Fabs(x-rhs.x)<eps&&Fabs(y-rhs.y)<eps;}
	bool operator != (const point &rhs)const{return Fabs(x-rhs.x)>eps||Fabs(y-rhs.y)>eps;}
	bool operator < (const point &rhs)const{return Fabs(y-rhs.y)<eps?x<rhs.x:y<rhs.y;} 
	double length(){return sqrt(sqr(x)+sqr(y));}
	point rev(){return point(y,-x);}
};
double dist(point x,point y){return (x-y).length();}
struct circle{
	point x;double r;circle(){r=0;}
	circle(double X,double Y,double R){x=point(X,Y);r=R;}
	point ask(double d){return point(x.x+r*cos(d),x.y+r*sin(d));}
	bool operator == (const circle &rhs)const{return x==rhs.x&&Fabs(r-rhs.r)<eps;}
}p[MAXN];
struct ming{
	circle x;double l,r;ming(){l=r=0;}
	ming(circle X,double L,double R){x=X;l=L;r=R;}
};
int n;double ans;
vector<ming>vec[MAXN<<2],tmpt;
pii work(circle x,circle y){
	if(x.r<y.r)swap(x,y);point z=y.x-x.x;
	if(z.length()<x.r-y.r)return mkpr(0,0);
	double agl=atan2(z.y,z.x),delta=acos((x.r-y.r)/z.length());
	double l=agl-delta,r=agl+delta;
	if(l<0)l+=Pi+Pi;else if(l>Pi+Pi)l-=Pi+Pi;
	if(r<0)r+=Pi+Pi;else if(r>Pi+Pi)r-=Pi+Pi;
	if(l>r)swap(l,r);return mkpr(l,r);
}
bool judge(circle x,circle y,double d){
	double A=cos(d),B=sin(d);
	double tmpx=A*x.x.x+B*x.x.y+x.r;
	double tmpy=A*y.x.x+B*y.x.y+y.r;
	return tmpx>tmpy;
}
void sakura(int rt,int l,int r){
	if(l==r){vec[rt].pb(ming(p[l],0,Pi+Pi));return ;}
	int mid=l+r>>1;sakura(lson,l,mid);sakura(rson,mid+1,r);
	int sizl=vec[lson].size(),sizr=vec[rson].size();
	for(int i=0,j=0;i<sizl&&j<sizr;){
		circle x=vec[lson][i].x,y=vec[rson][j].x;pii tmp=work(x,y);
		double L=max(vec[lson][i].l,vec[rson][j].l);
		double R=min(vec[lson][i].r,vec[rson][j].r);
		if(L<min(tmp.fir,R)){
			double md=(L+tmp.fir)/2.0;
			if(judge(x,y,md))tmpt.pb(ming(x,L,min(tmp.fir,R)));
			else tmpt.pb(ming(y,L,min(tmp.fir,R)));
		}
		if(max(tmp.fir,L)<min(tmp.sec,R)){
			double md=(tmp.fir+tmp.sec)/2.0;
			if(judge(x,y,md))tmpt.pb(ming(x,max(tmp.fir,L),min(tmp.sec,R)));
			else tmpt.pb(ming(y,max(tmp.fir,L),min(tmp.sec,R)));
		}
		if(max(tmp.sec,L)<R){
			double md=(tmp.sec+R)/2.0;
			if(judge(x,y,md))tmpt.pb(ming(x,max(tmp.sec,L),R));
			else tmpt.pb(ming(y,max(tmp.sec,L),R)); 
		}
		if(vec[lson][i].r<vec[rson][j].r)i++;else j++;
	}
	vec[lson].clear();vec[rson].clear();
	int siz=tmpt.size();ming now=tmpt[0];
	for(int i=1;i<siz;i++){
		if(tmpt[i].x==now.x)now.r=tmpt[i].r;
		else vec[rt].pb(now),now=tmpt[i];
	}
	vec[rt].pb(now);tmpt.clear();
}
signed main(){
	freopen("twenty.in","r",stdin);
	freopen("twenty.out","w",stdout);
	read(n);
	for(int i=1;i<=n;i++){
		int x,y,r;read(x);read(y);read(r);
		p[i]=circle(1.0*x,1.0*y,1.0*r);
	}
	sakura(1,1,n);int siz=vec[1].size();
	for(int i=0;i<siz;i++){
		ming u=vec[1][i];ans+=(u.r-u.l)*u.x.r;
		ming v=vec[1][(i+1)%siz];ans+=dist(u.x.ask(u.r),v.x.ask(v.l));
	}
	printf("%.8f\n",ans);
	return 0;
}

谢谢！！！