[硫化铂]题目名称
题目名称
题目概述

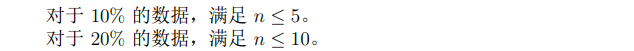

题解
看到这道题,我们显然不可能将每一个数都枚举一遍,也就是说,我们需要用更加简单的方式来表示我们这些数,生成函数正是一种很好的选择。
我们的生成函数
A
(
x
)
=
∑
i
=
1
n
∑
j
=
l
i
r
i
x
j
=
∑
i
=
1
n
x
l
−
x
r
+
1
1
−
x
A(x)=\sum_{i=1}^{n}\sum_{j=l_i}^{r_i}x^j=\sum_{i=1}^{n}\frac{x^l-x^{r+1}}{1-x}
A(x)=∑i=1n∑j=lirixj=∑i=1n1−xxl−xr+1,如果我们是在四个集合中选显然直接乘起来就可以了,但我们是要求从一个集合中选出四个不重复的数集,也就是说,我们得在上面的基础上去重。
去重后有,
A
n
s
=
[
x
s
]
1
24
(
A
4
(
x
)
−
6
A
(
x
2
)
A
2
(
x
)
+
3
A
2
(
x
2
)
+
8
A
(
x
3
)
A
(
x
)
−
6
A
(
x
4
)
)
Ans=[x^s]\frac{1}{24}(A^4(x)-6A(x^2)A^2(x)+3A^2(x^2)+8A(x^3)A(x)-6A(x^4))
Ans=[xs]241(A4(x)−6A(x2)A2(x)+3A2(x2)+8A(x3)A(x)−6A(x4))该式本身,是在枚举我们相同数的可能,使得最后只有全部不同的数集可以留下。
具体的计算方式,可以看成一个解线性方程组的形式,计算比较简单。
好的,我们已经得到了我们的答案式子,考虑如何计算这
x
s
x^s
xs处的系数。
显然,对于后三个式子的贡献,我们完全可以暴力枚举贡献到
x
s
x^s
xs处的值是多少。
那原来的区间合并即可。
而对于前面两个式子,就有点复杂了。
A
4
(
x
)
=
1
(
1
−
x
)
4
(
∑
x
l
−
x
r
+
1
)
4
=
∑
i
=
0
s
(
s
−
i
+
3
3
)
[
x
i
]
(
∑
x
l
−
x
r
+
1
)
4
A^4(x)=\frac{1}{(1-x)^4}(\sum x^l-x^{r+1})^4=\sum_{i=0}^s\binom{s-i+3}{3}[x^i](\sum x^l-x^{r+1})^4
A4(x)=(1−x)41(∑xl−xr+1)4=i=0∑s(3s−i+3)[xi](∑xl−xr+1)4
显然,对于后面那个四次方式,我们可以看成两个二次方式子乘起来,不妨记乘完后有
m
m
m项有系数,第
i
i
i项次数为
a
i
a_i
ai,系数为
f
i
f_i
fi。
进而有,
A
4
(
x
)
=
∑
a
i
+
a
j
⩽
s
f
i
f
j
(
s
−
a
i
−
a
j
+
3
3
)
A^4(x)=\sum_{a_i+a_j\leqslant s}f_if_j\binom{s-a_i-a_j+3}{3}
A4(x)=ai+aj⩽s∑fifj(3s−ai−aj+3)
如果有组合数的话是相当不好维护的,考虑拆一下,可得
A
4
(
x
)
=
∑
a
i
+
a
j
⩽
s
f
i
f
j
(
s
−
a
i
−
s
j
+
3
)
(
s
−
a
i
−
a
j
+
2
)
(
s
−
a
i
−
s
j
+
1
)
6
=
∑
a
i
+
a
j
⩽
s
f
i
f
j
(
s
−
a
i
)
3
+
(
s
−
a
i
)
2
(
6
−
3
a
j
)
+
(
s
−
a
i
)
(
11
−
12
a
j
+
3
a
j
2
)
+
(
3
−
a
j
)
(
2
−
a
j
)
(
1
−
a
j
)
6
A^4(x)=\sum_{a_i+a_j\leqslant s}f_if_j\frac{(s-a_i-s_j+3)(s-a_i-a_j+2)(s-a_i-s_j+1)}{6}\\ =\sum_{a_i+a_j\leqslant s}f_if_j\frac{(s-a_i)^3+(s-a_i)^2(6-3a_j)+(s-a_i)(11-12a_j+3a_j^2)+(3-a_j)(2-a_j)(1-a_j)}{6}
A4(x)=ai+aj⩽s∑fifj6(s−ai−sj+3)(s−ai−aj+2)(s−ai−sj+1)=ai+aj⩽s∑fifj6(s−ai)3+(s−ai)2(6−3aj)+(s−ai)(11−12aj+3aj2)+(3−aj)(2−aj)(1−aj)
这样的话,原来的组合数就被拆成了
4
4
4个与
a
i
a_i
ai与
a
j
a_j
aj有关的乘式。
如果我们要要求满足
a
i
+
a
j
⩽
s
a_i+a_j\leqslant s
ai+aj⩽s的条件,对于每个
i
i
i,相当于可以找到一个前缀和与它乘起来。
同样,我们考虑我们的
A
(
x
2
)
A
2
(
x
)
A(x^2)A^2(x)
A(x2)A2(x)咋办。
显然有
A
(
x
2
)
A
2
(
x
)
=
(
∑
x
2
l
−
x
2
r
+
2
)
(
∑
x
l
−
x
r
+
1
)
2
(
1
−
x
2
)
(
1
−
x
)
2
A(x^2)A^2(x)=\frac{(\sum x^{2l}-x^{2r+2})(\sum x^l-x^{r+1})^2}{(1-x^2)(1-x)^2}
A(x2)A2(x)=(1−x2)(1−x)2(∑x2l−x2r+2)(∑xl−xr+1)2
对于下面的分母,我们把它求一下逆,是
∑
i
=
1
+
∞
x
i
∑
j
=
1
⌊
i
2
⌋
(
i
−
2
j
+
1
)
\sum_{i=1}^{+\infty}x^i\sum_{j=1}^{\lfloor\frac{i}{2}\rfloor}(i-2j+1)
i=1∑+∞xij=1∑⌊2i⌋(i−2j+1)如果我们记
[
x
i
]
[x^i]
[xi]在右边的系数为
w
(
i
)
w(i)
w(i)的话,可以发现
w
(
i
)
w(i)
w(i)实际上是一个关于奇偶不同的函数。
对于奇数,
w
(
i
)
=
(
x
+
1
)
(
x
+
3
)
4
w(i)=\frac{(x+1)(x+3)}{4}
w(i)=4(x+1)(x+3)。
对于偶数,
w
(
i
)
=
(
x
+
2
)
2
4
w(i)=\frac{(x+2)^2}{4}
w(i)=4(x+2)2
我们的原式可以表示为,
A
(
x
2
)
A
2
(
x
)
=
∑
a
i
+
b
j
⩽
s
f
i
g
j
w
(
s
−
a
i
−
b
j
)
A(x^2)A^2(x)=\sum_{a_i+b_j\leqslant s}f_ig_jw(s-a_i-b_j)
A(x2)A2(x)=ai+bj⩽s∑figjw(s−ai−bj)同样,我们可以用上面的方法,将它化成许多个乘式。
∑
a
i
+
a
j
⩽
s
f
a
i
g
a
j
(
s
−
a
i
−
a
j
+
2
2
)
2
=
∑
a
i
+
a
j
⩽
s
f
a
i
g
a
j
(
s
−
a
i
)
2
−
2
(
s
−
a
i
)
(
a
j
−
2
)
+
(
a
j
−
2
)
2
4
)
∑
a
i
+
a
j
⩽
s
f
a
i
g
a
j
(
s
−
a
i
−
a
j
+
1
)
(
s
−
a
i
−
a
j
+
3
)
4
=
∑
a
i
+
a
j
⩽
s
f
a
i
g
a
j
(
s
−
a
i
)
2
+
(
4
−
2
a
j
)
(
s
−
a
i
)
+
(
3
−
a
j
)
(
1
−
a
j
)
4
\sum_{a_i+a_j\leqslant s}f_{a_i}g_{a_j}(\frac{s-a_i-a_j+2}{2})^2=\sum_{a_i+a_j\leqslant s}f_{a_i}g_{a_j}\frac{(s-a_i)^2-2(s-a_i)(a_j-2)+(a_j-2)^2}{4})\\ \sum_{a_i+a_j\leqslant s}f_{a_i}g_{a_j}\frac{(s-a_i-a_j+1)(s-a_i-a_j+3)}{4}=\sum_{a_i+a_j\leqslant s}f_{a_i}g_{a_j}\frac{(s-a_i)^2+(4-2a_j)(s-a_i)+(3-a_j)(1-a_j)}{4}
ai+aj⩽s∑faigaj(2s−ai−aj+2)2=ai+aj⩽s∑faigaj4(s−ai)2−2(s−ai)(aj−2)+(aj−2)2)ai+aj⩽s∑faigaj4(s−ai−aj+1)(s−ai−aj+3)=ai+aj⩽s∑faigaj4(s−ai)2+(4−2aj)(s−ai)+(3−aj)(1−aj)我们只要关于不同的奇偶性,做两个前缀和就可以了。
总时间复杂度
O
(
n
2
log
n
)
O\left(n^2\log n\right)
O(n2logn)。
很轻松得就可以通过此题。
源码
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#include<bits/stdc++.h>
using namespace std;
#define MAXN 805
#define MAXM 2000005
#define lowbit(x) (x&-x)
#define reg register
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
#define lson (rt<<1)
#define rson (rt<<1|1)
typedef long long LL;
typedef unsigned long long uLL;
typedef long double Ld;
typedef pair<int,int> pii;
const int INF=0x3f3f3f3f;
const int mo=998244353;
const int mod=1e5+7;
const int inv2=499122177;
const int inv3=332748118;
const double jzm=0.999;
const int zero=2000;
const int n1=10000;
const int orG=3,ivG=332748118;
const double Pi=acos(-1.0);
const double eps=1e-8;
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
template<typename _T>
void read(_T &x){
_T f=1;x=0;char s=getchar();
while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}
while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
x*=f;
}
template<typename _T>
void print(_T x){if(x<0)putchar('-'),print(-x);if(x>9)print(x/10);putchar(x%10+'0');}
LL gcd(LL a,LL b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*t*a%p;a=1ll*a*a%p;s>>=1;}return t;}
int n,S,ans,f[MAXM],g[MAXM][4],h[MAXM][4][2],tot,d[MAXM];
struct ming{int l,r;}a[MAXN],b[MAXN],c[MAXN];
signed main(){
freopen("count.in","r",stdin);
freopen("count.out","w",stdout);
read(n);read(S);const int inv6=1ll*inv2*inv3%mo;
for(int i=1;i<=n;i++)read(a[i].l),read(a[i].r);
if(S%4==0){
for(int i=1;i<=n;i++)
if(a[i].l<=S/4&&S/4<=a[i].r)
Add(ans,mo-6,mo);
}
if(S%2==0){
for(int i=1;i<=n;i++)b[i]=(ming){a[i].l,a[i].r};
for(int i=n;i>0;i--)c[n-i+1]=(ming){S/2-a[i].r,S/2-a[i].l};
for(int i=1,j=1;i<=n&&j<=n;){
int l=max(b[i].l,c[j].l);
int r=min(b[i].r,c[j].r);
if(l<=r)Add(ans,3ll*(r-l+1)%mo,mo);
if(b[i].r<c[j].r)i++;else j++;
}
}
for(int i=1;i<=n;i++)b[i]=(ming){3*a[i].l,3*a[i].r};
for(int i=n;i>0;i--)c[n-i+1]=(ming){S-a[i].r,S-a[i].l};
for(int i=1,j=1;i<=n&&j<=n;){
int l=max(b[i].l,c[j].l);
int r=min(b[i].r,c[j].r);
if(l<=r)Add(ans,8ll*(r/3-(l-1)/3)%mo,mo);
if(b[i].r<c[j].r)i++;else j++;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
d[++tot]=a[i].l+a[j].l,
d[++tot]=a[i].l+a[j].r+1,
d[++tot]=a[i].r+a[j].r+2;
sort(d+1,d+tot+1);tot=unique(d+1,d+tot+1)-d-1;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
int x=lower_bound(d+1,d+tot+1,a[i].l+a[j].l)-d;f[x]++;
int y=lower_bound(d+1,d+tot+1,a[i].r+a[j].r+2)-d;f[y]++;
int z=lower_bound(d+1,d+tot+1,a[i].l+a[j].r+1)-d;f[z]--;
int w=lower_bound(d+1,d+tot+1,a[i].r+a[j].l+1)-d;f[w]--;
}
for(int i=1;i<=tot;i++)f[i]=(f[i]%mo+mo)%mo;
for(int i=1;i<=tot;i++){
int tmp=f[i];
g[i][0]=add(g[i-1][0],tmp,mo);tmp=1ll*tmp*(S-d[i])%mo;
g[i][1]=add(g[i-1][1],tmp,mo);tmp=1ll*tmp*(S-d[i])%mo;
g[i][2]=add(g[i-1][2],tmp,mo);tmp=1ll*tmp*(S-d[i])%mo;
g[i][3]=add(g[i-1][3],tmp,mo);
}
for(int i=1,tmp;i<=tot;i++){
int t=upper_bound(d+1,d+tot+1,S-d[i])-d-1;
tmp=1ll*f[i]*inv6%mo;
Add(ans,1ll*tmp*g[t][3]%mo,mo);
tmp=1ll*f[i]*(mo+2-d[i])%mo*inv2%mo;
Add(ans,1ll*tmp*g[t][2]%mo,mo);
tmp=1ll*f[i]*(3ll*d[i]*d[i]%mo+mo-12ll*d[i]%mo+11)%mo*inv6%mo;
Add(ans,1ll*tmp*g[t][1]%mo,mo);
tmp=1ll*f[i]*(mo-d[i]+3)%mo*(mo-d[i]+2)%mo*(mo-d[i]+1)%mo*inv6%mo;
Add(ans,1ll*tmp*g[t][0]%mo,mo);
}
memset(g,0,sizeof(g));
for(int i=1;i<=tot;i++){
int j=d[i]&1,tmp=f[i];
h[i][0][j]=add(h[i-1][0][j],tmp,mo);tmp=1ll*(S-d[i]+mo)*tmp%mo;
h[i][1][j]=add(h[i-1][1][j],tmp,mo);tmp=1ll*(S-d[i]+mo)*tmp%mo;
h[i][2][j]=add(h[i-1][2][j],tmp,mo);
h[i][0][j^1]=h[i-1][0][j^1];
h[i][1][j^1]=h[i-1][1][j^1];
h[i][2][j^1]=h[i-1][2][j^1];
}
for(int i=1,j=S&1,tmp;i<=n;i++){
int x=upper_bound(d+1,d+tot+1,S-2*a[i].l)-d-1;
int y=upper_bound(d+1,d+tot+1,S-2*a[i].r-2)-d-1;
tmp=a[i].l+a[i].l;
Add(ans,mo-3ll*(tmp-2+mo)%mo*(tmp-2+mo)%mo*h[x][0][j]%mo*inv2%mo,mo);
Add(ans,3ll*(tmp-2+mo)%mo*h[x][1][j]%mo,mo);
Add(ans,mo-3ll*h[x][2][j]%mo*inv2%mo,mo);
Add(ans,mo-3ll*(mo+3-tmp)%mo*(mo+1-tmp)%mo*h[x][0][j^1]%mo*inv2%mo,mo);
Add(ans,mo-3ll*(mo+2-tmp)%mo*h[x][1][j^1]%mo,mo);
Add(ans,mo-3ll*h[x][2][j^1]%mo*inv2%mo,mo);
tmp=a[i].r+a[i].r+2;
Add(ans,3ll*(tmp-2+mo)%mo*(tmp-2+mo)%mo*h[y][0][j]%mo*inv2%mo,mo);
Add(ans,mo-3ll*(tmp-2+mo)%mo*h[y][1][j]%mo,mo);
Add(ans,3ll*h[y][2][j]%mo*inv2%mo,mo);
Add(ans,3ll*(mo+3-tmp)%mo*(mo+1-tmp)%mo*h[y][0][j^1]%mo*inv2%mo,mo);
Add(ans,3ll*(mo+2-tmp)%mo*h[y][1][j^1]%mo,mo);
Add(ans,3ll*h[y][2][j^1]%mo*inv2%mo,mo);
}
printf("%d\n",1ll*ans*qkpow(24,mo-2,mo)%mo);
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号