[硫化铂]叮叮车
叮叮车
题目概述

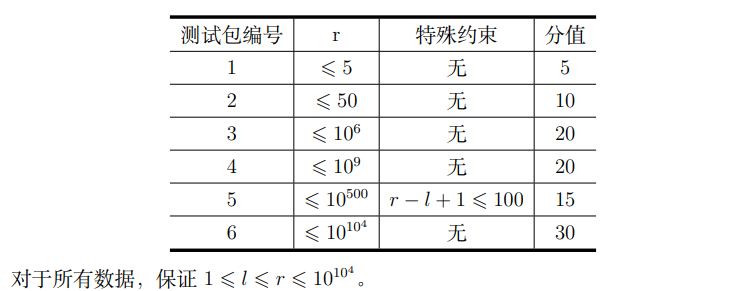
题解
首先,我们考虑最小的矩阵覆盖的方案数该怎么计算。
首先,覆盖一个大小为
n
n
n的阶梯矩形的最小数量肯定是
n
n
n。
因为不同的角肯定不可能出现在同一矩形内,至少需要
n
n
n个矩形,我们又很容易构造出一组只需要
n
n
n个的解,所以最小数量肯定为
n
n
n。
那我们又该怎么计数呢?
我们可以借助
d
p
dp
dp来统计,我们定义覆盖完前
i
i
i行,第
i
i
i行有
j
j
j个不同矩形的方案数为
d
p
i
,
j
dp_{i,j}
dpi,j。
我们如果已经覆盖好了前
n
−
1
n-1
n−1行,现在准备覆盖第
n
n
n行,那么我们转移的时候就要枚举那些矩形有哪些不能延伸到第
n
n
n行,这些就只能有第
n
n
n行新产生的矩形来覆盖。
因为第
n
n
n行只能新产生一个,所以去掉的矩形必然是第
n
n
n行的一个后缀,有转移方程式:
d
p
i
,
j
=
∑
k
=
j
−
1
i
−
1
d
p
i
−
1
,
k
dp_{i,j}=\sum_{k=j-1}^{i-1} dp_{i-1,k}
dpi,j=k=j−1∑i−1dpi−1,k尝试把第二维变成
i
−
j
i-j
i−j,那么有:
d
p
i
,
j
=
∑
k
=
0
min
(
i
−
1
,
j
)
d
p
i
−
1
,
k
dp_{i,j}=\sum_{k=0}^{\min(i-1,j)}dp_{i-1,k}
dpi,j=k=0∑min(i−1,j)dpi−1,k再把这放到网格图上,不就是往后走不能降低,这不是卡塔兰数吗?可以发现,
d
p
i
,
j
=
(
i
+
j
−
1
j
)
−
(
i
+
j
−
1
j
−
1
)
f
(
n
)
=
∑
i
=
0
n
−
1
d
p
i
,
j
=
∑
i
=
0
n
−
1
(
(
n
+
i
−
1
i
)
−
(
n
+
i
−
1
i
−
1
)
)
=
∑
i
=
0
n
−
1
(
n
−
1
+
i
n
−
1
)
−
∑
i
=
0
n
−
2
(
n
+
i
n
)
=
(
2
n
−
1
n
−
1
)
−
(
2
n
−
1
n
−
2
)
=
2
n
−
1
(
2
n
−
1
n
−
2
)
=
2
(
2
n
−
1
)
!
(
n
−
1
)
!
(
n
+
1
)
!
=
(
2
n
)
!
(
n
!
)
2
(
n
+
1
)
dp_{i,j}=\binom{i+j-1}{j}-\binom{i+j-1}{j-1}\\ f(n)=\sum_{i=0}^{n-1}dp_{i,j}=\sum_{i=0}^{n-1}\left(\binom{n+i-1}{i}-\binom{n+i-1}{i-1}\right)\\ =\sum_{i=0}^{n-1}\binom{n-1+i}{n-1}-\sum_{i=0}^{n-2}\binom{n+i}{n}=\binom{2n-1}{n-1}-\binom{2n-1}{n-2}\\ =\frac{2}{n-1}\binom{2n-1}{n-2}=\frac{2(2n-1)!}{(n-1)!(n+1)!}=\frac{(2n)!}{(n!)^2(n+1)}
dpi,j=(ji+j−1)−(j−1i+j−1)f(n)=i=0∑n−1dpi,j=i=0∑n−1((in+i−1)−(i−1n+i−1))=i=0∑n−1(n−1n−1+i)−i=0∑n−2(nn+i)=(n−12n−1)−(n−22n−1)=n−12(n−22n−1)=(n−1)!(n+1)!2(2n−1)!=(n!)2(n+1)(2n)!
我们要求的是
max
i
=
l
r
v
p
[
(
i
+
1
)
f
(
i
)
]
\max_{i=l}^rv_p[(i+1)f(i)]
maxi=lrvp[(i+1)f(i)],这恰好就乘上了一个
i
+
1
i+1
i+1呀。
那我们记我们
g
(
n
)
=
v
7
[
(
n
+
1
)
f
(
n
)
]
g(n)=v_7[(n+1)f(n)]
g(n)=v7[(n+1)f(n)],那么
g
(
n
)
=
v
7
[
(
2
n
)
!
(
n
!
)
2
]
g(n)=v_7[\frac{(2n)!}{(n!)^2}]
g(n)=v7[(n!)2(2n)!]。
我们算的是里面
7
7
7的数量,显然可以枚举里面
7
7
7的倍数个数。
g
(
n
)
=
∑
i
=
1
∞
⌊
2
n
7
i
⌋
−
2
⌊
n
7
i
⌋
=
∑
i
=
1
∞
[
2
(
n
%
7
i
)
⩾
7
i
]
g(n)=\sum_{i=1}^{\infty}\lfloor\frac{2n}{7^i}\rfloor-2\lfloor\frac{n}{7^i}\rfloor=\sum_{i=1}^{\infty}[2(n\%7^i)\geqslant7^i]
g(n)=i=1∑∞⌊7i2n⌋−2⌊7in⌋=i=1∑∞[2(n%7i)⩾7i]可以发现,我们的答案一定是
log
7
R
\log_7 R
log7R级别的。
上面的式子说的是,我们将一个数
7
7
7进制化了后,如果某一位后面的翻倍能够进位,就会有
1
1
1的贡献。
这不是可以数位 dp 吗?
我们定义
d
p
i
,
0
/
1
,
0
/
1
,
0
/
1
dp_{i,0/1,0/1,0/1}
dpi,0/1,0/1,0/1,表示转移到第
i
i
i位,是否触底,是否触顶,是否需要后面进位是的最大贡献。
转移方式只需要枚举后面加位的值,根据其关于
3
3
3的大小转移即可。
当然,最开始要将
l
l
l与
r
r
r变成
7
7
7进制。
时间复杂度 O ( log 7 R ) O\left(\log_7 R\right) O(log7R),当然,要带一个不小的常数。
源码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> pii;
#define MAXN 20005
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
const int lim=1000000;
template<typename _T>
void read(_T &x){
_T f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
x*=f;
}
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1;}return t;}
int lena,lenb,dp[MAXN][2][2][2],ans,a[MAXN],b[MAXN],sta[MAXN],stak;
char astr[MAXN],bstr[MAXN];
int main(){
freopen("dingdingcar.in","r",stdin);
freopen("dingdingcar.out","w",stdout);
scanf("%s\n%s",astr+1,bstr+1);
lena=(int)strlen(astr+1);
lenb=(int)strlen(bstr+1);
memset(dp,-0x3f,sizeof(dp));int x=0;
reverse(astr+1,astr+lena+1);
reverse(bstr+1,bstr+lenb+1);
for(int i=1;i<=lena;i++)a[i]=astr[i]-'0';
for(int i=1;i<=lenb;i++)b[i]=bstr[i]-'0';
for(int i=1;i<=lena;i+=6){stak++;for(int j=5;j>=0;j--)sta[stak]=10*sta[stak]+a[i+j];}lena=0;
while(stak){
for(int i=stak;i>0;i--)sta[i]=x*lim+sta[i],x=sta[i]%7,sta[i]/=7;
a[++lena]=x;x=0;while(stak&&!sta[stak])stak--;
}
for(int i=1;i<=lenb;i+=6){stak++;for(int j=5;j>=0;j--)sta[stak]=10*sta[stak]+b[i+j];}lenb=0;
while(stak){
for(int i=stak;i>0;i--)sta[i]=x*lim+sta[i],x=sta[i]%7,sta[i]/=7;
b[++lenb]=x;x=0;while(stak&&!sta[stak])stak--;
}
int len=max(lena,lenb);dp[len][1][1][1]=1;dp[len][1][1][0]=0;
for(int i=len;i>0;i--)
for(int S1=0;S1<2;S1++)
for(int S2=0;S2<2;S2++){
for(int j=0;j<7;j++){
if((S1&&j<a[i])||(S2&&j>b[i]))continue;
int s1=S1&(j==a[i]),s2=S2&(j==b[i]);
if(j<3)dp[i-1][s1][s2][0]=max(dp[i-1][s1][s2][0],dp[i][S1][S2][0]),
dp[i-1][s1][s2][1]=max(dp[i-1][s1][s2][1],dp[i][S1][S2][0]+1);
if(j==3)dp[i-1][s1][s2][0]=max(dp[i-1][s1][s2][0],dp[i][S1][S2][0]),
dp[i-1][s1][s2][1]=max(dp[i-1][s1][s2][1],dp[i][S1][S2][1]+1);
if(j>3)dp[i-1][s1][s2][0]=max(dp[i-1][s1][s2][0],dp[i][S1][S2][1]),
dp[i-1][s1][s2][1]=max(dp[i-1][s1][s2][1],dp[i][S1][S2][1]+1);
}
}
for(int S1=0;S1<2;S1++)
for(int S2=0;S2<2;S2++)
ans=max(ans,dp[0][S1][S2][0]);
printf("%d\n",ans);
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号