[航海协会]逆转函数
逆转函数
题目概述

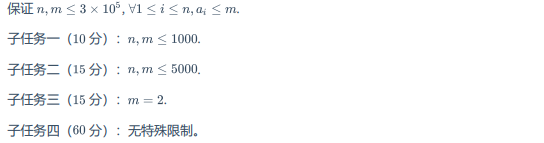
题解
首先我们观察一下这个
m
=
2
m=2
m=2的点,我们记
(
x
,
y
)
(x,y)
(x,y),表示
f
(
0
)
=
x
,
f
(
1
)
=
y
f(0)=x,f(1)=y
f(0)=x,f(1)=y。考虑
(
0
,
0
)
,
(
0
,
1
)
,
(
1
,
0
)
,
(
1
,
1
)
(0,0),(0,1),(1,0),(1,1)
(0,0),(0,1),(1,0),(1,1)的映射情况产生的贡献。
显然,
(
0
,
0
)
,
(
1
,
1
)
(0,0),(1,1)
(0,0),(1,1)显然就只有全
0
0
0和全
1
1
1的段产生贡献。
而
(
0
,
1
)
(0,1)
(0,1)则必须是回文串才有贡献,如果不回文,那么也就是
f
(
0
)
=
1
,
f
(
1
)
=
0
f(0)=1,f(1)=0
f(0)=1,f(1)=0了,这个可以马拉车处理。
而
(
1
,
0
)
(1,0)
(1,0)则是要求必须全都不同的回文,我们理性猜测一下,它也是可以马拉车的。
也就是说,按我们
0
0
0和
1
1
1匹配的规则,如果一个大回文串中包含一个小回文串,那么这个小回文串翻折到另一边后仍然是回文的,在我们
(
1
,
0
)
(1,0)
(1,0)的规则下它是相当于平移的。
容易发现,任意一种匹配方式都是可以马拉车的。
那我们来找一找其他可行的子区间的匹配规则。
重要的一点是如果
f
(
A
)
=
B
f(A)=B
f(A)=B,那么一定有
f
(
B
)
=
A
f(B)=A
f(B)=A,毕竟如果
A
A
A回文后匹配到
B
B
B,
B
B
B匹配的也一定是
A
A
A。
由此可以得到我们马拉车的扩增原理,只要看这两个点是否已经有其他的匹配。
不过如果记录每个点的匹配的话未免也太累了,我们可以记录一下它的前驱与后继,匹配
x
x
x与
y
y
y需要检查它们的前驱后继位置,是在
[
x
,
y
]
[x,y]
[x,y]中的话就要求这两个位置是回文的。
同样,我们的答案实际上是
f
f
f值尚未确定的点的个数的幂,每次匹配产生的贡献为
[
n
x
t
x
⩾
y
]
+
[
p
r
e
y
<
x
]
[nxt_x\geqslant y]+[pre_y< x]
[nxtx⩾y]+[prey<x],加上去即可。
但是我们还得算所有子区间的答案和呀,我们得知道我们被翻转到
2
m
i
d
−
i
2mid-i
2mid−i后已经匹配了多少个数,以及它的每个子区间的数的数量。
注意,反转后是不能超过
m
i
d
mid
mid对应回文串的右边界的。
不妨将我们所有的回文串建一棵树,树上每个节点记录回文串的长度与确定了
f
f
f的数的数量。
翻转我们可以通过倍增跳到我们在原树上的位置,再向外扩展时就等于不断新增儿子节点。
由于我们的右边界是在不断右移的,移动一次只会多一个节点,显然树的大小是
O
(
n
)
O(n)
O(n)级别的。
然后就把我们每个回文串放在树上的节点上,通过一个回文串产生的贡献是从它这里一直到根的路径上的所有点的贡献和,可以最后一起统计。
时间复杂度 O ( n log n ) O\left(n\log n\right) O(nlogn)。
源码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> pii;
#define MAXN 600005
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
#define lowbit(x) (x&-x)
const int mo=998244353;
template<typename _T>
void read(_T &x){
_T f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
x*=f;
}
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1;}return t;}
int n,m,a[MAXN],ans,head[MAXN],pre[MAXN],nxt[MAXN],idx,sum[MAXN];
int len[MAXN],num[MAXN],f[MAXN][20],pos[MAXN],b[MAXN],tot,pw[MAXN];
int cmp(int x,int y){
if(!b[x]||!b[y])return b[x]==b[y];
if(nxt[x]>=y&&pre[y]<=x)return 1;
if(nxt[x]>=y||pre[y]<=x)return 0;
return nxt[x]+pre[y]==x+y;
}
int main(){
freopen("invfunc.in","r",stdin);
freopen("invfunc.out","w",stdout);
read(n);read(m);
pw[0]=1;for(int i=1;i<=n;i++)pw[i]=1ll*m*pw[i-1]%mo;
for(int i=1;i<=n;i++)read(a[i]),b[++tot]=a[i],++tot;tot--;
for(int i=1;i<=tot;i++)pre[i]=head[b[i]],nxt[pre[i]]=i,head[b[i]]=i;
for(int i=1;i<=tot;i++)if(!nxt[i])nxt[i]=tot+1;
pos[1]=++idx;len[idx]=num[idx]=1;sum[idx]++;
for(int i=2,mid=1;i<=tot;i++){
if(mid+len[pos[mid]]<=i)
pos[i]=++idx,len[idx]=1,num[idx]=i&1;
else{
pos[i]=pos[mid+mid-i];
for(int j=18;j>=0;j--)
if(i+len[f[pos[i]][j]]>=mid+len[pos[mid]])
pos[i]=f[pos[i]][j];
}
if(mid+len[pos[mid]]<=i+len[pos[i]]){
mid=i;int now=pos[i];
while(i+len[now]<=tot&&i-len[now]>0&&cmp(i-len[now],i+len[now])){
now=++idx;len[now]=len[pos[i]]+1;num[now]=num[pos[i]];
if(b[i-len[now]+1]&&nxt[i-len[now]+1]>=i+len[now]-1)num[now]++;
if(b[i+len[now]-1]&&pre[i+len[now]-1]<i-len[now]+1)num[now]++;
f[now][0]=pos[i];pos[i]=now;
for(int i=1;i<19;i++)f[now][i]=f[f[now][i-1]][i-1];
}
}
if(i+len[pos[i]]&1)sum[f[pos[i]][0]]++;else sum[pos[i]]++;
}
for(int i=idx;i>0;i--)
Add(ans,1ll*sum[i]*pw[m-num[i]]%mo,mo),sum[f[i][1]]+=sum[i];
printf("%d\n",ans);
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号