[航海协会]数论
数论

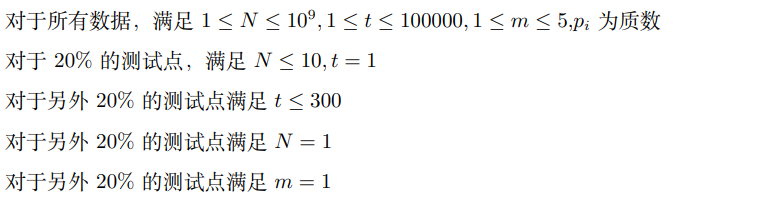
题解
容易发现发现我们的
F
F
F是一个积性函数,显然,组成它的
ϕ
\phi
ϕ都是积性的,它们于是卷起来的,
F
F
F肯定是积性的。
所以我们的
G
(
N
)
=
∑
∑
k
i
=
N
∏
F
(
p
i
k
i
)
G(N)=\sum_{\sum k_i=N}\prod F(p_i^{k_i})
G(N)=∑∑ki=N∏F(piki),但这样好像不是特别好看的样子,我们可以考虑转化成生成函数的形式。
我们定义
F
i
=
∑
j
=
0
∞
F
(
p
i
j
)
x
j
F_i=\sum_{j=0}^{\infty} F(p_i^j)x^j
Fi=∑j=0∞F(pij)xj,容易发现,
F
i
=
(
∑
j
=
0
∞
ϕ
(
p
i
j
)
x
j
)
m
=
(
1
+
∑
j
=
1
∞
(
p
i
j
−
p
i
j
−
1
)
x
j
)
m
=
(
1
−
x
1
−
p
i
x
)
m
G
(
N
)
=
[
x
N
]
∏
i
=
1
t
F
i
=
[
x
N
]
∏
i
=
1
t
(
1
−
x
1
−
p
i
x
)
m
F_i=(\sum_{j=0}^{\infty}\phi(p_i^j)x^j)^m=(1+\sum_{j=1}^{\infty}(p_i^j-p_i^{j-1})x^j)^m=(\frac{1-x}{1-p_ix})^m\\ G(N)=[x^N]\prod_{i=1}^tF_i=[x^N]\prod_{i=1}^t\left(\frac{1-x}{1-p_ix}\right)^m\\
Fi=(j=0∑∞ϕ(pij)xj)m=(1+j=1∑∞(pij−pij−1)xj)m=(1−pix1−x)mG(N)=[xN]i=1∏tFi=[xN]i=1∏t(1−pix1−x)m现在我们的目的是计算这个分式的第
N
N
N项,显然
N
N
N这么大,不太可能暴力乘出来。
一种较为常见的计算分式远项的方法是线性递推,我们把上面的式子化一化,
也就是将原来的分式简单变化一下
F
=
g
(
x
)
f
(
x
)
=
f
(
−
x
)
g
(
x
)
f
(
−
x
)
f
(
x
)
=
g
′
(
x
)
f
′
(
x
2
)
F=\frac{g(x)}{f(x)}=\frac{f(-x)g(x)}{f(-x)f(x)}=\frac{g'(x)}{f'(x^2)}
F=f(x)g(x)=f(−x)f(x)f(−x)g(x)=f′(x2)g′(x),这样的话,下面就只剩下偶数次项了。
如果我们要求的是第
N
N
N项的
N
N
N为偶数,那么上面的
g
′
(
x
)
g'(x)
g′(x)就只有偶数项有用,递归到,同样
N
N
N为奇数,上面也只有奇数项有用。
可以尝试递归求解,
[
x
N
]
g
(
x
)
f
(
x
)
=
{
[
x
N
2
]
f
e
v
e
n
′
(
x
)
g
′
(
x
)
(
2
∣
N
)
[
x
N
−
1
2
]
f
o
d
d
′
(
x
)
g
′
(
x
)
(
2
∤
N
)
[x^N]\frac{g(x)}{f(x)}=\left\{\begin{array}{cc}[x^{\frac{N}{2}}]\frac{f'_{even}(x)}{g'(x)} & (2\mid N)\\ [x^{\frac{N-1}{2}}]\frac{f'_{odd}(x)}{g'(x)} & (2\nmid N)\end{array}\\\right.
[xN]f(x)g(x)={[x2N]g′(x)feven′(x)[x2N−1]g′(x)fodd′(x)(2∣N)(2∤N)每次递归相当于都要做一次多项式乘法,将
f
f
f与
g
g
g变成
f
′
f'
f′和
g
′
g'
g′,同时将
N
N
N除以二。
直到我们的
N
N
N变为
0
0
0,这时候我们的答案就是
[
x
0
]
G
(
x
)
[
x
0
]
F
(
x
)
\frac{[x^0]G(x)}{[x^0]F(x)}
[x0]F(x)[x0]G(x)了。
时间复杂度 O ( m t log n log t ) O\left(mt\log n\log t\right) O(mtlognlogt)
源码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> pii;
typedef unsigned int uint;
#define MAXN 500005
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
const LL INF=0x3f3f3f3f3f3f3f3f;
const int mo=998244353;
const int orG=3,ivG=332748118;
template<typename _T>
void read(_T &x){
_T f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
x*=f;
}
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
LL gcd(LL a,LL b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1;}return t;}
int n,t,m,p[MAXN],ff[MAXN],Cg[10][10],f[MAXN],g[MAXN];
int F[MAXN<<2],G[MAXN<<2],H[MAXN<<2],rev[MAXN<<2];
void init(){
ff[1]=1;for(int i=2;i<=m*t;i++)ff[i]=1ll*(mo-mo/i)*ff[mo%i]%mo;
for(int i=0;i<=m;i++){
Cg[i][0]=Cg[i][i]=1;
for(int j=1;j<i;j++)
Cg[i][j]=add(Cg[i-1][j-1],Cg[i-1][j],mo);
}
}
void NTT(int *A,const int lim,const int typ){
for(int i=0;i<lim;i++)if(i<rev[i])swap(A[i],A[rev[i]]);
for(int mid=1;mid<lim;mid<<=1){
const int W=qkpow(typ^1?ivG:orG,(mo-1)/(mid<<1),mo);
for(int i=mid<<1,j=0;j<lim;j+=i)
for(int Wn=1,k=j;k<j+mid;k++,Wn=1ll*W*Wn%mo){
int x=A[k],y=1ll*Wn*A[k+mid]%mo;
A[k]=add(x,y,mo);A[k+mid]=add(x,mo-y,mo);
}
}
if(typ^-1)return ;int tp=qkpow(lim,mo-2,mo);
for(int i=0;i<lim;i++)A[i]=1ll*tp*A[i]%mo;
}
void sakura(int l,int r){
if(l==r){
for(int i=1,now=1;i<=m;i++)
now=1ll*(mo-p[l])*now%mo,
f[i+(l-1)*m]=1ll*Cg[m][i]*now%mo;
return ;
}
int mid=l+r>>1;sakura(l,mid);sakura(mid+1,r);
int lim=1,L=0;while(lim<=(r-l+1)*m)lim<<=1,L++;
for(int i=0;i<lim;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<L-1);
for(int i=1;i<=(mid-l+1)*m;i++)F[i]=f[i+(l-1)*m];F[0]=1;NTT(F,lim,1);
for(int i=1;i<=(r-mid)*m;i++)G[i]=f[i+mid*m];G[0]=1;NTT(G,lim,1);
for(int i=0;i<lim;i++)F[i]=1ll*F[i]*G[i]%mo;NTT(F,lim,-1);
for(int i=1;i<=(r-l+1)*m;i++)f[i+(l-1)*m]=F[i];
for(int i=0;i<lim;i++)F[i]=G[i]=0;
}
int main(){
//freopen("math.in","r",stdin);
//freopen("math.out","w",stdout);
read(n);read(t);read(m);init();
for(int i=1;i<=t;i++)read(p[i]);f[0]=1;sakura(1,t);
for(int i=0,now=1;i<=m*t;i++)
g[i]=(i&1)?mo-now:now,now=1ll*(m*t-i)*ff[i+1]%mo*now%mo;
int lim=1,L=0;while(lim<=2*m*t)lim<<=1,L++;
for(int i=0;i<lim;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<L-1);
while(n){
for(int i=0;i<=m*t;i++)F[i]=f[i],H[i]=(i&1)?mo-f[i]:f[i],G[i]=g[i],f[i]=g[i]=0;
NTT(F,lim,1);NTT(G,lim,1);NTT(H,lim,1);
for(int i=0;i<lim;i++)F[i]=1ll*F[i]*H[i]%mo;NTT(F,lim,-1);
for(int i=0;i<lim;i++)G[i]=1ll*G[i]*H[i]%mo;NTT(G,lim,-1);
for(int i=0;i<=2*m*t;i+=2)f[i>>1]=F[i];
for(int i=n&1;i<=2*m*t;i+=2)g[i>>1]=G[i];
for(int i=0;i<lim;i++)F[i]=G[i]=H[i]=0;n>>=1;
}
printf("%lld\n",1ll*g[0]*qkpow(f[0],mo-2,mo)%mo);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号