[航海协会]序列计数问题
序列计数问题
题目概述

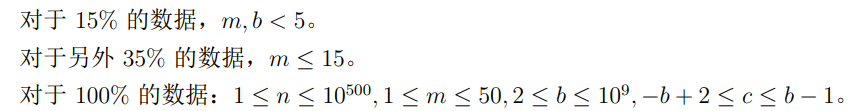
题解
首先看到这题目,应该比较容易想到生成函数。
第
i
i
i个数的生成函数显然是
F
i
=
∑
j
=
0
b
i
−
c
x
j
=
1
−
x
b
i
−
c
+
1
1
−
x
F_i=\sum_{j=0}^{b^i-c}x^j=\frac{1-x^{b^i-c+1}}{1-x}
Fi=∑j=0bi−cxj=1−x1−xbi−c+1
答案要求
∑
x
i
<
n
\sum x_i<n
∑xi<n,相当于就是全部乘起来,做个前缀和取第
n
−
1
n-1
n−1项,
其中,我们定义
f
(
S
)
=
∑
x
∈
S
b
x
f(S)=\sum_{x\in S}b^x
f(S)=∑x∈Sbx表示
A
n
s
=
[
x
n
−
1
]
∏
i
=
1
m
1
−
x
b
i
−
c
+
1
(
1
−
x
)
m
+
1
=
[
x
n
−
1
]
∑
S
⊂
U
(
−
1
)
∣
S
∣
x
f
(
S
)
−
(
c
−
1
)
∣
S
∣
(
1
−
x
)
m
+
1
A
n
s
=
∑
S
⊂
U
(
−
1
)
∣
S
∣
(
n
+
m
−
1
+
(
c
−
1
)
∣
S
∣
−
f
(
S
)
m
)
Ans=[x^n-1]\frac{\prod_{i=1}^m 1-x^{b^i-c+1}}{(1-x)^{m+1}}=[x^n-1]\frac{\sum_{S\subset U}(-1)^{|S|}x^{f(S)-(c-1)|S|}}{(1-x)^{m+1}}\\ Ans=\sum_{S\subset U}(-1)^{|S|}\binom{n+m-1+(c-1)|S|-f(S)}{m}
Ans=[xn−1](1−x)m+1∏i=1m1−xbi−c+1=[xn−1](1−x)m+1∑S⊂U(−1)∣S∣xf(S)−(c−1)∣S∣Ans=S⊂U∑(−1)∣S∣(mn+m−1+(c−1)∣S∣−f(S))直接枚举集合
S
S
S可以做到
O
(
2
m
m
)
O\left(2^mm\right)
O(2mm),但都做到这里了我们何必暴力枚举集合呢?
考虑再给它化一下,
A
n
s
=
1
m
!
∑
S
⊂
U
(
n
+
m
−
1
+
(
c
−
1
)
∣
S
∣
−
f
(
S
)
)
m
‾
Ans=\frac{1}{m!}\sum_{S\subset U}(n+m-1+(c-1)|S|-f(S))^{\underline m}
Ans=m!1S⊂U∑(n+m−1+(c−1)∣S∣−f(S))m显然可以数位
d
p
dp
dp,我们可以将后面的下降幂看成一个多项式,然后
d
p
dp
dp维护。
为了同时保证后面下降幂那东西不小于
m
m
m,我们枚举的
f
(
S
)
f(S)
f(S)显然得有一个上限,不能超过
n
+
m
−
1
+
(
c
−
1
)
∣
S
∣
n+m-1+(c-1)|S|
n+m−1+(c−1)∣S∣,这个上限与
∣
S
∣
|S|
∣S∣有关,所以我们可以考虑先枚举
∣
S
∣
|S|
∣S∣,再根据当前的上限数位
d
p
dp
dp。
定义
d
p
i
,
j
,
k
,
0
/
1
dp_{i,j,k,0/1}
dpi,j,k,0/1表示在前
i
i
i位中,选择了
j
j
j位,并且是否达到上限的集合
S
S
S的
f
(
S
)
k
f(S)^k
f(S)k次方之和。
转移显然就是每次枚举是否加入当前的
2
i
2^i
2i嘛,但由于需要转移每个次方的值,我们的复杂度会达到惊人的
O
(
m
5
)
O\left(m^5\right)
O(m5),考虑优化。
注意到
2
−
b
⩽
c
⩽
b
−
1
2-b\leqslant c\leqslant b-1
2−b⩽c⩽b−1,显然,当
b
>
2
b>2
b>2时,有
(
b
n
−
c
+
1
)
⩾
∑
i
=
1
n
−
1
(
b
i
−
c
+
1
)
(b^n-c+1)\geqslant \sum_{i=1}^{n-1}(b^i-c+1)
(bn−c+1)⩾∑i=1n−1(bi−c+1)。
也就是说,我们可以尝试求出当前能够选择的字典序最大
S
S
S,显然,比这字典序小的
S
S
S都是可以被选择的。
这样我们就可以只对一个
n
n
n进行数位
d
p
dp
dp了,优化到
O
(
m
4
)
O\left(m^4\right)
O(m4)。
对于
b
=
2
,
c
=
1
b=2,c=1
b=2,c=1时,上面的结论依旧成立。
对于
b
=
2
,
c
=
0
b=2,c=0
b=2,c=0时,一种简单的方法就是先将所有小于
n
n
n的
f
(
S
)
f(S)
f(S)全部计算,再减掉
f
(
S
)
+
∣
S
∣
⩾
n
f(S)+|S|\geqslant n
f(S)+∣S∣⩾n的部分的贡献。
但我们不妨继续思考一下我们上面的方法是否能够得到正确的答案,毕竟笔者懒得分类讨论。
我们定义
A
>
B
A>B
A>B为集合
A
A
A的字典序比集合
B
B
B的字典序大。
如果
S
′
⊂
S
S'\subset S
S′⊂S,由于
∀
i
∈
[
1
,
∞
)
,
b
i
−
c
+
1
>
0
\forall i\in[1,\infty),b^i-c+1>0
∀i∈[1,∞),bi−c+1>0,所以
f
(
S
)
>
f
(
S
′
)
∧
S
>
S
′
f(S)>f(S')\wedge S>S'
f(S)>f(S′)∧S>S′
所以如果我们直接枚举每个点加入是否符合
<
n
<n
<n的话一定可以找到满足
f
(
S
)
<
n
f(S)<n
f(S)<n的字典序最大集合
S
S
S。
显然,对于
S
′
<
S
,
f
(
S
′
)
<
f
(
S
)
S'<S,f(S')<f(S)
S′<S,f(S′)<f(S),由于
∣
S
′
∣
−
∣
S
∣
⩽
m
|S'|-|S|\leqslant m
∣S′∣−∣S∣⩽m,所以
f
(
S
′
)
+
∣
S
′
∣
−
f
(
S
)
−
∣
S
∣
⩽
m
f(S')+|S'|-f(S)-|S|\leqslant m
f(S′)+∣S′∣−f(S)−∣S∣⩽m。
这也就是说上面的
n
+
m
−
1
+
(
c
−
1
)
∣
S
∣
−
f
(
S
)
⩾
0
n+m-1+(c-1)|S|-f(S)\geqslant 0
n+m−1+(c−1)∣S∣−f(S)⩾0。
如果
(
c
−
1
)
∣
S
∣
−
f
(
S
)
⩾
n
(c-1)|S|-f(S)\geqslant n
(c−1)∣S∣−f(S)⩾n,也不过是一个在
[
0
,
m
)
[0,m)
[0,m)之间数的
m
m
m次下降幂罢了,它肯定经过
0
0
0,贡献也自然是
0
0
0,没啥用。
所以采用我们上面的方法是一定可以得到正确答案的。
时间复杂度 O ( m 3 ) O\left(m^3\right) O(m3)。
源码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> pii;
typedef unsigned int uint;
#define MAXN 505
#define MAXM (1<<15)+5
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
const int lim=1000000;
const LL INF=0x3f3f3f3f3f3f3f3f;
const int mo=1e9+7;
template<typename _T>
void read(_T &x){
_T f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
x*=f;
}
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
LL gcd(LL a,LL b){return !b?a:gcd(b,a%b);}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1;}return t;}
int N,m,B,c,len,a[MAXN],b[MAXN*4],lena,totb,g[55];
int pwb[55],ff[55],ans,dp[55][55][2],C[55][55],f[55];
char str[MAXN];bool mark[55];
void work(){
for(int i=1;i<=totb;i++){
if(b[i]<0)b[i+1]--,b[i]+=B;
if(b[i]>=B)b[i+1]++,b[i]-=B;
}
while(b[totb+1])totb++;
while(totb&&!b[totb])totb--;
}
signed main(){
//freopen("seqcnt.in","r",stdin);
//freopen("seqcnt.out","w",stdout);
scanf("%s",str+1);read(m);read(B);read(c);
len=(int)strlen(str+1);pwb[0]=1;
for(int i=0;i<=m;i++){
C[i][0]=C[i][i]=1;
for(int j=1;j<i;j++)
C[i][j]=add(C[i-1][j-1],C[i-1][j],mo);
}
ff[1]=1;for(int i=2;i<=m;i++)ff[i]=1ll*(mo-mo/i)*ff[mo%i]%mo;
for(int i=1;i<=m;i++)pwb[i]=1ll*B*pwb[i-1]%mo;
for(int i=1;i<=len;i++)N=(10ll*N+str[i]-'0')%mo;
for(int i=len,now=1,j=1;i>0;i--){
a[j]+=now*(str[i]-'0'),now*=10;
lena=j;if(now==lim)now=1,j++;
}
while(lena){
int now=0;
for(int i=lena;i>0;i--){
LL tp=1ll*lim*now+a[i];
now=tp%B;a[i]=tp/B;
}
b[++totb]=now;
while(lena&&!a[lena])lena--;
}
b[1]--;work();Add(N,m,mo);
b[1]+=(c-1);work();
if(totb>m+1)mark[m+1]=1;
else for(int i=m;i>0;i--){
//for(int j=1;j<=totb;j++)printf("%d ",b[j]);puts("");
bool flag=0;for(int j=i+1;j<=totb;j++)if(b[j])flag|=1;
if(!flag)continue;b[i+1]--;mark[i]=1,b[1]+=(c-1),work();
if(!totb||b[totb]<0)break;
}
dp[m][0][!mark[m+1]]=1;
for(int i=m;i>0;i--){
int tp=(1ll*pwb[i]+mo-c+1)%mo;g[0]=1;
for(int j=1;j<=m;j++)g[j]=1ll*tp*g[j-1]%mo;
for(int j=0;j<=m;j++)for(int k=0;j+k<=m;k++)
Add(dp[i-1][j+k][0],mo-1ll*dp[i][j][0]*g[k]%mo*C[j+k][k]%mo,mo);
for(int j=0;j<=m;j++)Add(dp[i-1][j][0],dp[i][j][0],mo);
if(mark[i])for(int j=0;j<=m;j++)for(int k=0;j+k<=m;k++)
Add(dp[i-1][j+k][1],mo-1ll*dp[i][j][1]*g[k]%mo*C[j+k][k]%mo,mo);
for(int j=0;j<=m;j++)Add(dp[i-1][j][!mark[i]],dp[i][j][1],mo),g[j]=0;
}
g[0]=1;
for(int i=1;i<=m;i++)for(int j=m;j>0;j--)
Add(g[j],1ll*add(N,mo-i,mo)*g[j-1]%mo,mo);
for(int i=0;i<=m;i++){
Add(f[i],dp[0][i][0],mo),
Add(f[i],dp[0][i][1],mo);
if(i&1)f[i]=mo-f[i];
}
for(int i=0;i<=m;i++)Add(ans,1ll*g[i]*f[m-i]%mo,mo);
for(int i=1;i<=m;i++)ans=1ll*ff[i]*ans%mo;
printf("%d\n",ans);
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号