[航海协会]SSSP

SSSP

题目概述

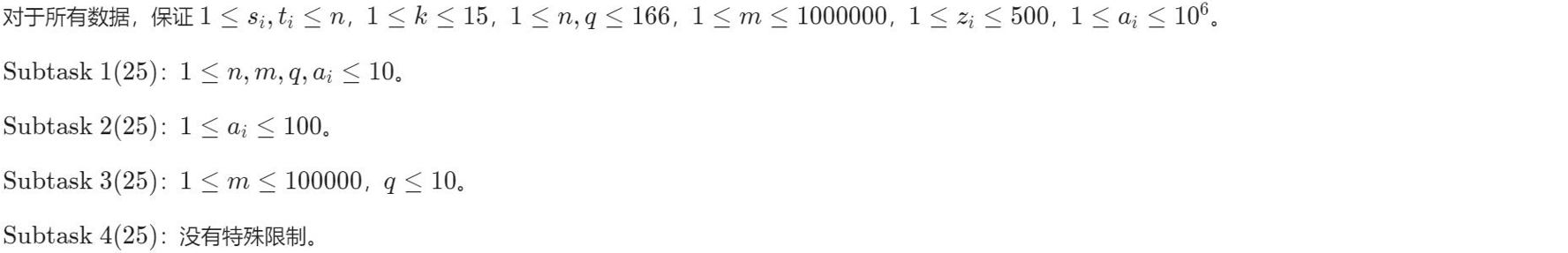
题解

首先让我们看看这道题，应该很容易先想到一个比较暴力的思路，就是不断让所有点都往前走一条边，然后维护到所有点前$K$小的路径长度。
显然，再之后的路径无论怎么走都无法成为前$K$小了，无论如何都至少有$K$条比它们小的路径，所以只维护前$K$小即可。
但这样做显然是$O\left(qm{K}^2\right)$的，考虑怎么优化。
可以发现，它们的转移都是符合矩阵的性质的，可以考虑把转移放到矩阵上去，然后就可以用矩阵维护了，先预处理出倍增矩阵，这样询问的时候也就只需要乘向量。
复杂度成功被优化到了$O\left((n+q)n^2{K}^2\log a+mK\right)$，显然还是跑不过考虑继续优化。

可以发现，${\sum }_{k=1}^n{M}_{i,k}{M}_{k,j}$都是会转移贡献到$M_{i,j}^{\prime }$，我们只用维护它的前$K$小，那么一种经典方法就是先将$M_{i,k}{M}_{k,j}$的最小的值放到堆里面去，每次选出所有数中最小的一个，放到$M_{i,j}^{\prime }$里面去，它是由$M_{i,k}{M}_{k,j}$构成的，然后将$M_{i,k}$或者$M_{k,j}$稍微调大一点放到堆里面去。
这样每次稍微调大肯定都是找到的稍微大点的一个，所有都必然在某个时刻被加入。
由于我们只找前$K$大，所以除了最开始加入的，都只会再加入$K$个。
这样的时间复杂度是$O\left((n+q)n(n+K)\log n\log a+mK\right)$。
但它还是会$T$的，显然，这里的复杂度瓶颈是在那个$n\log n$上面的，由于最开始的元素是比较多的，考虑线性建堆。
也就是后序遍历二叉树，当加入两个儿子的父亲时，看父亲是不是比儿子小，如果是就把较小的儿子调上来，父亲扔下去。
这样的话建堆是$\sum O(\frac{in}{2^i})\approx O(n)$的，复杂度就被优化到$O\left((n+q)n(n+K\log n)\log a+mK\right)$了，看上去就很能过了。
但如果你交上去的话你会发现你还是会被卡常了。
观察一下，我们的堆还是太大了，明明值需要前$K$小，却达到了$O\left(n\right)$级别的大小。
考虑$nth\_element$对于我们最开始的数组求出前$K$小再建堆，这样就会快不少。
时间复杂度也就达到了$O\left((n+q)n(n+K\log K)\log a+mK\right)$，基本不会被卡常了。

上面已经说了，时间复杂度$O\left((n+q)n(n+K\log K)\log a+mK\right)$。

源码

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> pii;
#define MAXM 2000005
#define pb push_back
#define mkpr make_pair
#define fir first
#define sec second
const int INF=0x3f3f3f3f;
template<typename _T>
void read(_T &x){
   _T f=1;x=0;char s=getchar();
   while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
   while('0'<=s&&s<='9'){x=(x<<3)+(x<<1)+(s^48);s=getchar();}
   x*=f;
}
template<typename _T>
_T Fabs(_T x){return x<0?-x:x;}
int add(int x,int y,int p){return x+y<p?x+y:x+y-p;}
void Add(int &x,int y,int p){x=add(x,y,p);}
int qkpow(int a,int s,int p){int t=1;while(s){if(s&1)t=1ll*a*t%p;a=1ll*a*a%p;s>>=1;}return t;}
int n,m,Q,logtime,tota,totb,root,totc;
struct ming{
    int x,y,z,w;ming(){}
    ming(int X,int Y,int Z,int W){x=X;y=Y;z=Z;w=W;}
    bool operator < (const ming &rhs)const{return w<rhs.w;}
}a[205];
struct node{
    int dis[18];node(){}
    void clear(){for(int i=1;i<=15;i++)dis[i]=INF;}
};
class Treap{
    private:
        int tot,lson[55],rson[55];ming tr[55];
    public:
        void check(int rt){
            if(!lson[rt]&&!rson[rt])return ;
            int lw=lson[rt]?tr[lson[rt]].w:INF;
            int rw=rson[rt]?tr[rson[rt]].w:INF;
            if(lw<=rw&&lw<tr[rt].w){swap(tr[rt],tr[lson[rt]]),check(lson[rt]);if(tr[lson[rt]].w>INF-1)lson[rt]=0;}
            else if(rw<tr[rt].w){swap(tr[rt],tr[rson[rt]]),check(rson[rt]);if(tr[rson[rt]].w>INF-1)rson[rt]=0;}
        }
        void build(int &rt,int l,int r){
            int mid=l+r>>1;rt=++tot;tr[rt]=a[mid];
            if(l<mid)build(lson[rt],l,mid-1);
            if(r>mid)build(rson[rt],mid+1,r);
            check(rt);
        }
        ming ask(){return tr[root];}
        void pop(){tr[root].w=INF;check(root);if(tr[root].w>INF-1)root=0;}
        void insert(ming aw){
            if(!root){root=++tot;tr[tot]=aw;return ;}
            int now=root;
            while(1){
                if(tr[now].w>aw.w)swap(tr[now],aw);
                if(lson[now]&&rson[now]){now=(rand()&1)?lson[now]:rson[now];continue;}
                if(!lson[now])lson[now]=++tot;else rson[now]=++tot;
                tr[tot]=aw;break;
            }
        }
        void clear(){for(int i=0;i<=tot;i++)lson[i]=rson[i]=0;root=tot=0;}
}T;
struct matrix{
    node c[170][170];matrix(){}
    void clear(){
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                c[i][j].clear();
    }
    matrix operator * (const matrix &rhs){
        matrix res;res.clear();
        for(int i=1;i<=n;i++){
            if(logtime&&i!=logtime)continue;
            for(int j=1;j<=n;j++){
                root=tota=0;int mx=0;
                for(int k=1;k<=n;k++){
                    int tmp=c[i][k].dis[1]+rhs.c[k][j].dis[1];
                    if(tmp<INF-1)a[++tota]=ming(1,1,k,tmp);
                }
                if(tota>15)nth_element(a+1,a+16,a+tota+1),tota=15;
                if(tota)T.build(root,1,tota);
                for(int k=1;k<=15;k++){
                    if(!root){res.c[i][j].dis[k]=INF;continue;}
                    ming t=T.ask();T.pop();res.c[i][j].dis[k]=t.w;
                    if(t.x<15&&t.y==1){
                        int tmp=c[i][t.z].dis[t.x+1]+rhs.c[t.z][j].dis[t.y];
                        if(tmp<INF-1)T.insert(ming(t.x+1,t.y,t.z,tmp));
                    }
                    if(t.y<15){
                        int tmp=c[i][t.z].dis[t.x]+rhs.c[t.z][j].dis[t.y+1];
                        if(tmp<INF-1)T.insert(ming(t.x,t.y+1,t.z,tmp));
                    }
                }
                T.clear();
            }
        }
        return res;
    }
}M[22],Ans;
int main(){
    //freopen("sssp.in","r",stdin);
    //freopen("sssp.out","w",stdout);
    read(n);read(m);read(Q);M[0].clear();
    for(int i=1;i<=m;i++){
        int u,v,w;read(u);read(v);read(w);
        M[0].c[u][v].dis[16]=w;
        for(int j=15;j>0;j--)
            if(M[0].c[u][v].dis[j]>M[0].c[u][v].dis[j+1])
                swap(M[0].c[u][v].dis[j],M[0].c[u][v].dis[j+1]);
    }
    for(int i=1;i<20;i++)M[i]=M[i-1]*M[i-1];
    for(int i=1;i<=Q;i++){
        int s,t,A,K;read(s);read(t);read(A);read(K);
        Ans.clear();Ans.c[s][s].dis[1]=0;logtime=s;
        for(int j=0;j<20;j++)if(A&(1<<j))Ans=Ans*M[j];
        int res=Ans.c[s][t].dis[K];
        if(res>INF-1)puts("-1");else printf("%d\n",res);
    }
    return 0;
}

谢谢！！！