做题集——(高精度+找规律)Friends

题目：Friends

题面：

Sample Input

2
0
2

Ouput

Case #1: 1
Case #2: 1024

题意：

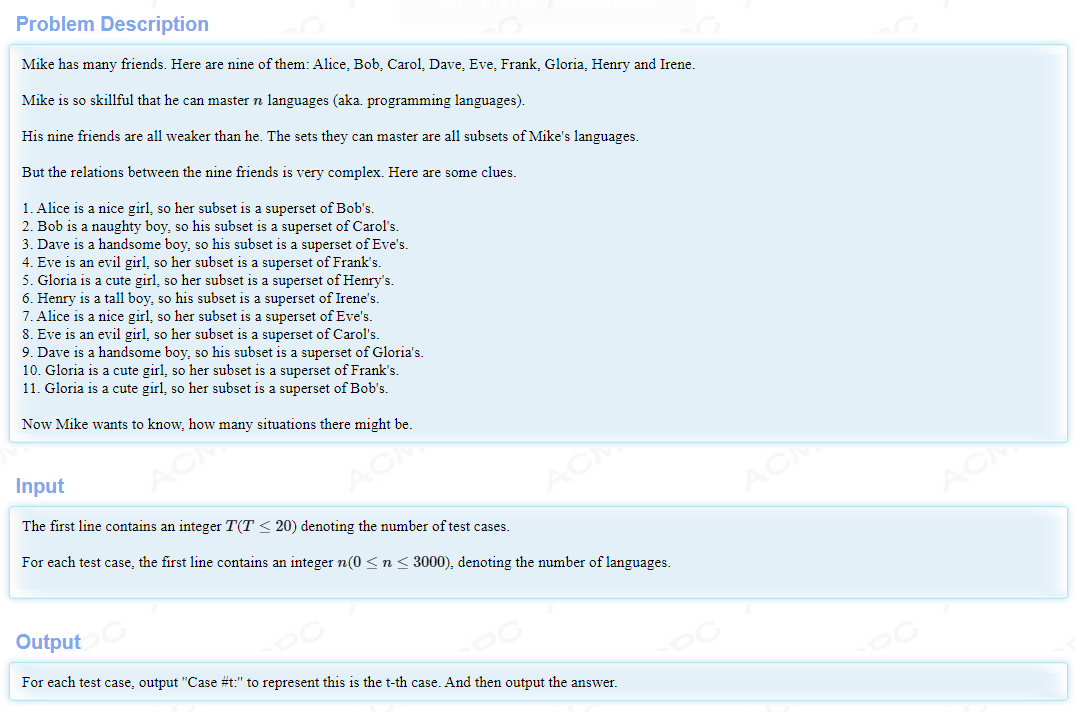
　　M会使用n种语言，M的九个朋友会的语言都是M的子集，并且给出九个朋友会的语言的关系，求出总共有多少种可能

思路：

　　目前为止还不知道怎么做到的找规律，反正结论是32^{n种可能，不过除了该题还有一个要注意的点，就是32}n太大，一个longlong装不下，需要使用高精度的方法进行处理

Code：

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 3e4;
const int MOD = 1000;
int num[MAXN];
int len;
void solve(int n) {
    memset(num, 0, sizeof(num));
    num[1] = 1; len = 1;
    for (int i = 1; i <= n; i++) {
        int c = 0;
        for (int j = 1; j <= len; j++) {
            num[j] *= 32;
            num[j] += c;
            c = num[j] / MOD;
            num[j] %= MOD;
        }
        while (c) {
            num[++len] = c % MOD;
            c /= MOD;
        }
    }
}

int main() {
    int T; cin >> T;
    int n;
    for (int t = 1; t <= T; t++) {
        scanf("%d", &n);
        solve(n);
        printf("Case #%d: " , t);
        for(int i = len;i > 0;i--) {
            if (i != len) printf("%03d", num[i]);
            else printf("%d" , num[i]);
        }
        putchar('\n');
    }

    return 0;
}

思路：

　　也可以使用矩阵快速幂，定义大数的乘法

Code：

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 3e4;
const int MOD = 1000;   //一个num装的最大数字, 可以再大一些

struct BigNum {
    int num[MAXN];
    int len;
    void Mult(const BigNum& T) {
        int tmp[MAXN] = {0}; //先要进行临时存储
        for (int i = 1; i <= len; i++) {
            for (int j = 1; j <= T.len; j++) {
                tmp[i + j - 1] += num[i] * T.num[j];
                tmp[i + j] += tmp[i + j - 1] / MOD; //进位的直接加上去
                tmp[i + j - 1] %= MOD;
            }
        }
        //按最大长度来, 然后递减
        int lent = len + T.len + 1;
        while (!tmp[lent] && lent > 1) lent--;
        for (int i = 1; i <= lent; i++) num[i] = tmp[i];
        len = lent;    
    }
    void Print() {
        printf("%d", num[len]);
        for (int i = len - 1; i; i--) {
            printf("%03d", num[i]);
        }
        putchar('\n');
    }
};
int main() {
    int T; cin >> T;
    int n;
    for (int t = 1; t <= T; t++) {
        scanf("%d", &n);
        BigNum a, ans;
        a.num[1] = 32; a.len = 1;
        ans.num[1] = 1; ans.len = 1; 
        while (n) {
            if (n & 1) ans.Mult(a);
            n >>= 1;
            a.Mult(a);
        }
        printf("Case #%d: " , t);
        ans.Print();   
    }

    return 0;
}