傅里叶变换的物理意义

用三角函数表示周期函数

傅里叶的相关理论始于下面假设：对于周期为1的信号$f(t)$，可以由不同频率的三角函数组成，

$f(t) = \frac{a_0}{2}+\displaystyle{\sum^{\infty}_{k=1}}(a_kcos(2\pi kt)+b_ksin(2\pi kt))$

组成的基础波形为一个信号对，分别为$cos(2\pi t)$以及$sin(2\pi t)$，波形的频率覆盖范围为$k=1,2,3,\cdots$（角频率为$2\pi k$），在这些频率上的系数（即振幅）对为$(a_1,b_1),(a_2,b_2),(a_3,b_3),\cdots$。

 

 

傅里叶级数

上面的式子可以进一步推导成傅里叶级数形式：

$f(t) = \displaystyle{\sum^{\infty}_{k=-\infty}C_ke^{2\pi ikt} }$

从这个表现形式看出，组成的基础波形为$e^{2\pi it}$，波形的频率覆盖范围是$k=0,\pm 1,\pm 2,\pm 3,\cdots$（角频率为$2\pi k$），在这些频率上的系数为$C_0, C_{\pm 1}, C_{\pm 2}, C_{\pm 3}, \cdots$，这些系数由下面的式子得到：

$C_k = \displaystyle{\int_{0}^{1}f(t)e^{-2\pi ikt}dt}$

如果我们把记录信号在时间上的值的函数$f(t)$称作该信号在时域上的表现的话，那么该信号在频率$k$上的系数$C_k$就是该信号在频域上的表现。傅里叶系数的物理意义就是信号在对应频率上的振幅。

 

 

傅里叶变换

为了把傅里叶的理论应用到一般信号，我们把周期扩展到$T\to\infty$，那么信号$f(t)$的傅里叶级数变成：

$f(t) = \displaystyle{\lim_{T\to\infty}\sum_{k=-\infty}^{\infty}C_ke^{2\pi i\frac{k}{T}t} }$

此时的傅里叶系数变成：

$C_k = \displaystyle{\lim_{T\to\infty}\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-2\pi i\frac{k}{T}t}dt }$

可以看到由于信号$f(t)$在$(-\infty,\infty)$上是可积的，当$T$被扩展到无穷的时候傅里叶系数$C_k$被稀释成$0$了，因此可以认为一般信号在各个频率上的傅里叶系数（振幅）为$0$。这种结果对于我们进行傅里叶分析是没有用处的，因此有了如下傅里叶变换：

令

$\displaystyle{\mathcal{F} f(s) =C_k \times T = \int_{-\infty}^{\infty}e^{-2\pi i st}f(t)dt }$

其中$s = \frac{k}{T}$，即原本是离散的频率$k$被扩展成了覆盖$(-\infty,\infty)$的连续变量$s$，因此可以得到

$f(t) = \displaystyle{\int_{-\infty}^{\infty}\mathcal{F} f(s)e^{2\pi ist}ds }$

其中$ds = \frac{1}{T}$，$s$是可以覆盖所有频率的变量。

$\displaystyle{\mathcal{F} f(s) }$就是信号$f(t)$的傅里叶变换。但此时傅里叶变换不再具有傅里叶系数的物理意义。

 

 

傅里叶变换的物理意义

Plancherel's Formula

Plancherel's Formula有如下定义：

$\displaystyle{\int_{-\infty}^{\infty}f(t)\overline{g(t)}\,dt=\int_{-\infty}^{\infty}F(s)\overline{G(s)}\,ds}$

证明：

$\begin{align*}\int_{-\infty}^{\infty}f(t)\overline{g(t)}\,dt
&=\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}F(s)e^{2\pi ist}\,ds \right )\overline{\left(\int_{-\infty}^{\infty}G(s')e^{2\pi is't}\,ds' \right )}\,dt \\
&=\int_{-\infty}^{\infty}\left(\int_{-\infty}^{\infty}F(s)e^{2\pi ist}\,ds \right )\left(\int_{-\infty}^{\infty}\overline{G(s')}e^{-2\pi is't}\,ds' \right )\,dt \\
&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F(s)\overline{G(s')}\int_{-\infty}^{\infty}e^{2\pi i(s-s')t}\,dt\,ds'\,ds \\
&=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F(s)\overline{G(s')}\delta(s'-s)\,ds'\,ds\qquad \mathcal{F}e^{2\pi ist} = \delta(s'-s)\ ,variable\ is\ s'\\
&=\int_{-\infty}^{\infty}F(s)\int_{-\infty}^{\infty}\overline{G(s')}\delta(s'-s)\,ds'\,\,ds \\
&=\int_{-\infty}^{\infty}F(s)\,\overline{G(s)}\,ds \qquad \delta\ shift\ theorem\\
\end{align*}$

 

Energy Spectral Density

根据Plancherel's Formula，可以得到

$\begin{align*}
\int_{-\infty}^{\infty}|f(t)|^2\,dt
&=\int_{-\infty}^{\infty}f(t)\overline{f(t)}\,dt\\
&=\int_{-\infty}^{\infty}F(s)\overline{F(s)}\,ds\\
&=\int_{-\infty}^{\infty}|F(s)|^2\,ds
\end{align*}$

假设有一个物理实验，目的是测量电流通过某个电阻时所产生的能量，已知电阻两端的电势差会随着时间变化，为$V(t)$，电阻的阻抗为$R$，那么所产生的能量为：

$\displaystyle{\int_{-\infty}^{\infty}\frac{V(t)^2}{R}dt}$

此时回顾上面所得到的式子

$\displaystyle{\int_{-\infty}^{\infty}|f(t)|^2\,dt=\int_{-\infty}^{\infty}|F(s)|^2\,ds}$

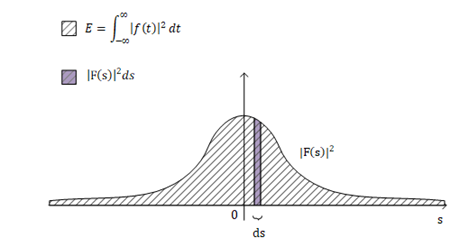
首先是等号左边：其中信号$f(t)$可以认为是电势差随着时间的变化，如果我们忽略电阻抗后，可以认为产生的能量为$\displaystyle{\int_{-\infty}^{\infty}|f(t)|^2\,dt}$。等号右边的$s$，按照我们前面的讨论，$s$代表的就是频率，因此$|F(s)|^2$可以看作信号的能量在频域上的能量密度函数（Energy Spectral Density）。如下图，宽度为$ds$的频率所蕴含的能量大小为$|F(s)|^2ds$

如果我们对信号进行带通滤波，那么被过滤掉的频率就无法再继续贡献能量，ESD上就会缺少被过滤掉的频率所对应的区域，相应地傅里叶变换也会缺少被过滤掉的频率所对应的区域。