tick学习笔记

X-DataInitiative/tick 是一个关于 Hawkes Process 的 Python 实现，核心功能是给定 Point process 的若干样本，他能计算出一个 Non parametric 的 Hawkes Process 来拟合这个 Point process。

本文的任务就是搞明白这个 package，从而把这个 package 改良以应用到预测订单（市价单、限价单、撤单）流的强度。

Point Process & Counting Process

Point Process 是指某个空间中分布的随机点的集合，当这个空间是时间轴的时候，我们可以认为在随机发生事件，发生的时间是 \(T_1, T_2, ...\)

Counting Process \(N_t\) 是 Point Process 的另一种等价刻画，他也是定义在一个空间上的随机变量族，当这个空间是时间轴的时候，可以视为一个随机过程， \(N_t\) 表示到时间 \(t\) 位置，发生了多少个事件。

\[N_t:= \sum_{i=1} [T_i \leq t] \]

Counting Process 性质：

1. \(N(t)\) 为非负整数
2. \(N(t)\) 单调不减
3. \(N(t)-N(s)\) 代表 \((s,t]\) 内事件发生次数

我们可以把市价单，限价单，撤单当做事件序列分别建立他们的 Point Process 和 Counting Process.

Poisson Process

Poisson Process 和 Hawkes Process 都是一种 Point Process，先来看比较简单的 Poisson Process 来引入一些直观的概念。

Poisson Distribution

概率论的内容，可以视作在描述一个很长的时间段内，一个很小概率发生事件发生的次数（即二项分布 $n \rightarrow \infty $ ， \(p\) 很小时的近似）

\[P(X=k)=\frac{\lambda^k e^{-\lambda}}{k!} \]

由 \(e^x\) 在 \(0\) 处的泰勒展开容易计算这个分布的期望就是 \(\lambda\)

Homogeneous Poisson process

Counting Process \({N(t), t \geq 0}\) 是 Homogeneous Poisson process， 当且仅当满足

1. \(N(0)=0\)
2. 独立增量: \(0<t_1<t_2<...<t_k(k \geq 1), N(t_1), N(t_2)-N(t_1),...,N(t_k)-N(t_{k-1})\) 相互独立
3. 平稳增量：\(s<t, N(t)-N(s)\) 和 \(N(t-s)\) 分布相同
4. \(P\{N(t+s)-N(s)=k\}=(\frac{(\lambda t)^k e^{-\lambda t}}{k!})\) ，即 \(N(t)\) 是参数为 \(\lambda t\) 的 Poissonb分布
5. *（4的等价定义）\(X_i:=\) 第 \(i\) 个事件和 \(i-1\) 个事件的发生间隔，则 $X_i \sim Exp(\lambda) $

4 与 5 的等价性：

\[P(X_1>t)=P(N_t=0) \\ = \frac{(\lambda t)^0 e^{-\lambda t}}{0!}=e^{-\lambda t} \]

即 \(X_1 \sim Exp(\lambda)\) ，同理考虑 \(X_2\)

\[P(X_2 >t |X_1=s)=P(N(t+s)-N(s)=0|X_1=s) \\ =\frac{(\lambda t)^0 e^{-\lambda t}}{0!}=e^{-\lambda t} \]

同理可得所有 \(X_i\) 都符合 \(Exp(\lambda)\)

这说明了 Poisson 分布的无记忆性，即当前时间和这个过程之前发生过什么完全没有关系。

结合第 4 条定义与 Poisson 分布代表了一段时间内事件发生次数，我们可以知道 \(\lambda\)
其实代表了事件的强度，因为 \(N(\lambda)\) 本质是参数为 \(\lambda\) 的随机过程单位时间内事件发生的次数。

（ \(N(\lambda t)\) 是 \([0,t]\) 内发生的次数， \(\frac{N(\lambda t)}{t}=N(\lambda)\) 是平均发生次数。）由期望可以得到，事件期望单位时间发生 \(\lambda\) 次，发生事件的间隔的期望时间是 \(1/\lambda\)

6.*（4的等价定义） $$P(N(t+h)-N(t)=1)=\lambda h+o(h) \ P(N(t+h)-N(t)=2)=o(h)$$
即当时间间隔 \(h\) 很小时，发生一次的概率就是 \(\lambda h\) ,发生两次的概率可以视为没有。

Non homogeneous Poisson process

就是没有平稳增量的 homogeneous Poisson process， 即事件的强度 \(\lambda\) 不再是一个常数，而是一个随时间变化的函数 \(\lambda(t)\) 。这时要记住第 6 条定义的含义， \(\lambda(t)\) 本质是 \(t\) 时间发生事件的瞬时概率。

这时有 $$N(s+t)-N(s) \sim P(m(s,s+t))$$
即符合参数为 \(m(s,s+t)\) 的 Poisson 分布 $$m(s,s+t)=\int_s^{s+t} \lambda(x) dx$$

Hawkes Process

与 Poisson Process 不同， Hawkes Process 是一个关联历史的 Counting Process,他去掉了 Poisson Process 的独立增量和平稳增量，但仍然能用事件强度去描述这个过程。

\[\lambda(t|\mathcal H_t)=\mu(t)+\sum_{t>t_i} g(t-t_i) \]

以后为方便， \(\lambda(t|\mathcal H_t)\) 记作 \(\lambda(t)\) 。

\(\mu(t)\) 是一个确定的函数，是这个事件的背景强度函数

\(t_i < t\) 是在枚举所有 \(t\) 之前发生的事情，他以 \(g(t-t_i)\) 的强度影响当前时刻的事件强度，一般认为 \(g\) 是单调递减的，即越靠前发生的事情对当前影响越小， \(g\) 称作核函数 (kernal) 。

MLE

最大似然估计（Maximum Likelihood Estimation,MLE）是一种最基本的在已知数据时估计参数的方法。复制一段理解什么是似然的话：

概率是在特定环境下某件事情发生的可能性，也就是结果没有产生之前依据环境所对应的参数来预测某件事情发生的可能性，比如抛硬币，抛之前我们不知道最后是哪一面朝上，但是根据硬币的性质我们可以推测任何一面朝上的可能性均为50%，这个概率只有在抛硬币之前才是有意义的，抛完硬币后的结果便是确定的；而似然刚好相反，是在确定的结果下去推测产生这个结果的可能环境（参数），还是抛硬币的例子，假设我们随机抛掷一枚硬币1,000次，结果500次人头朝上，500次数字朝上（实际情况一般不会这么理想，这里只是举个例子），我们很容易判断这是一枚标准的硬币，两面朝上的概率均为50%，这个过程就是我们根据结果来判断这个事情本身的性质（参数），也就是似然。

概率记作 \(P(x|\theta)\) ，\(\theta\) 是参数，\(x\) 是事件。

似然记作 \(\mathcal L(\theta|x)\) , x 是已经发生的事件。

\(\mathcal L(\theta|x) = \frac{P(\theta, x)}{P(x)}=P(\theta,x)\)，因为 \(x\) 已经发生，所以 \(P(x)=1\)。

\(P(\theta,x)=P(x|\theta)=P_{\theta}(x)\) ，即 \(\theta\) 似然其实等于参数取 \(\theta\) 是发生事件 \(x\) 的概率。

最大似然估计就是给定一个事件集，取这个概率最大的时候的参数为 \(\theta\) 的过程。

一般似然函数会涉及多个独立的事件，即 \(\mathcal L=\prod_{i=1}^N p_i\) .

一般会取对简化， \(log(\mathcal L)=\sum_{i=1}^N log(p_i)\)

然后经典的操作是把 \(log(\mathcal L)\) 对每个参数求偏导，让偏导为0，解方程得到参数。

以下是点过程的似然函数的推导，AI生成。

点过程似然函数的推导

---

1. 点过程的基本定义

设观测到的事件发生时刻为 $ t_1, t_2, \dots, t_n $，时间窗口为 \([0, T]\)。点过程的特性由条件强度函数描述：

\[\lambda(t \mid H_t) = \lim_{\Delta t \to 0} \frac{P(\text{事件在 } [t, t+\Delta t) \text{ 内发生} \mid H_t)}{\Delta t}, \]

其中 $ H_t $ 表示截至时间 $ t $ 的历史事件信息。

---

2. 联合概率密度的离散近似

将时间轴 \([0, T]\) 划分为长度为 $ \Delta t $ 的小区间，共 $ M = T / \Delta t $ 个区间：

• ​有事件发生：在区间 \([t_k, t_k + \Delta t)\) 内发生事件，概率近似为 $ \lambda(t_k \mid H_{t_k}) \Delta t $。
• ​无事件发生：概率近似为 $ 1 - \lambda(t_k \mid H_{t_k}) \Delta t $。

联合概率密度近似为：

\[L \approx \left( \prod_{i=1}^n \lambda(t_i \mid H_{t_i}) \Delta t \right) \cdot \prod_{k \neq \text{事件区间}} \left( 1 - \lambda(t_k \mid H_{t_k}) \Delta t \right). \]

---

3. 连续极限（$ \Delta t \to 0 $）

• ​无事件区间的极限：

  \[\sum_{k \neq \text{事件区间}} \log \left( 1 - \lambda(t_k \mid H_{t_k}) \Delta t \right) \approx -\int_0^T \lambda(t \mid H_t) \, dt, \]

  对应指数项：

  \[\exp\left( -\int_0^T \lambda(t \mid H_t) \, dt \right). \]

• ​事件时刻的极限：
  保留乘积项：

  \[\prod_{i=1}^n \lambda(t_i \mid H_{t_i}). \]

---

4. 最终似然函数

合并两部分得到：

\[L = \left( \prod_{i=1}^n \lambda(t_i \mid H_{t_i}) \right) \cdot \exp\left( -\int_0^T \lambda(t \mid H_t) \, dt \right). \]

---

5. 对数似然函数

取对数后形式为：

\[\ell = \sum_{i=1}^n \log \lambda(t_i \mid H_{t_i}) - \int_0^T \lambda(t \mid H_t) \, dt. \]

EM

期望最大（Expectation Maximization）算法是一种从不完全数据或有数据丢失的数据集（存在隐含变量）中求解概率模型参数的最大似然估计方法。

他的目的也是使似然最大，但是由于数据集缺失了一些标签，不能直接使用MLE。

示例说明：硬币抛掷实验

---

​1. 已知硬币标签的实验数据

硬币	结果	统计
1	正正反正反	3正-2反
2	反反正正反	2正-3反
1	正反反反反	1正-4反
2	正反反正正	3正-2反
1	反正正反反	2正-3反

参数估计：

• 硬币1：共抛掷15次，正面出现6次
  \[P_1 = \frac{3 + 1 + 2}{15} = 0.4 \]

• 硬币2：共抛掷10次，正面出现5次
  \[P_2 = \frac{2 + 3}{10} = 0.5 \]

---

​2. 隐变量引入：未知硬币标签的实验数据

硬币	结果	统计
Unknown	正正反正反	3正-2反
Unknown	反反正正反	2正-3反
Unknown	正反反反反	1正-4反
Unknown	正反反正正	3正-2反
Unknown	反正正反反	2正-3反

隐变量定义：

• 隐变量 \(z = (z_1, z_2, z_3, z_4, z_5)\)，其中 \(z_i \in \{1, 2\}\)，表示第 \(i\) 轮实验使用的硬币。
• 目标：通过估计 \(z\) 的值，进一步估计 \(P_1\) 和 \(P_2\)。

做法

EM的实现是典型的梯度下降方法。

假设观测数据为\(X\)，隐变量为\(Z\)，参数为\(\theta\)。

1. 先随机一组 \(\theta\) ，计算出在 \(\theta\) 情况下 \(Z\) 的分布。
2. 计算 \(Z\) 分布下的似然函数的期望。
3. 让这个期望最大，解得一组新的 \(\theta\) ,再返回第二步，直到 \(\theta\) 收敛。

EM算法的证明步骤

1. 问题定义与下界构造

假设观测数据为\(X\)，隐变量为\(Z\)，参数为\(\theta\)。目标是最大化对数似然函数：

\[\log p(X|\theta) = \log \sum_Z p(X,Z|\theta) \]

引入隐变量分布\(Q(Z)\)，利用Jensen不等式构造下界：

\[\begin{aligned} \log p(X|\theta) &= \log \sum_Z Q(Z) \frac{p(X,Z|\theta)}{Q(Z)} \\ &\geq \sum_Z Q(Z) \log \frac{p(X,Z|\theta)}{Q(Z)} \triangleq \mathcal{L}(Q,\theta) \end{aligned} \]

其中\(\mathcal{L}(Q,\theta)\)是对数似然的下界。

2. E步：优化\(Q(Z)\)

为使得下界紧贴原函数，选择\(Q(Z) = p(Z|X,\theta^{(t)}) = \frac{P(Z,X|\theta)}{P(X|\theta)}\)，此时Jensen不等式取等号 (\(\log \frac{P(X,Z|\theta)}{Q(Z)}=\log P(X|\theta)\)，全部相等，故Jensen不等于取等号)：

\[\log p(X|\theta^{(t)}) = \mathcal{L}(Q^{(t+1)},\theta^{(t)}) \]

这表明在\(\theta^{(t)}\)处，下界与原函数值相等。

这步的实际含义是，直接计算 \(\theta^{(t)}\) 的情况下 \(Z\) 的分布 \(Q^{(t+1)}(Z)\)，可以保证 \(\mathcal{L}(Q^{(t+1)},\theta^{(t)})\) 取到下界：这一步是关键步骤，不仅因为 \(Q^{(t+1)}(Z)\) 容易计算，也保证了任意取一组新的 \(\theta^{(t+1)}\) 似然函数都能变大。

3. M步：优化参数\(\theta\)

固定\(Q^{(t+1)}(Z)\)，更新参数：

\[\theta^{(t+1)} = \arg\max_\theta \mathcal{L}(Q^{(t+1)},\theta) \]

由于\(\mathcal{L}(Q^{(t+1)},\theta)\)可分解为：

\[\mathcal{L}(Q^{(t+1)},\theta) = \mathbb{E}_{Q^{(t+1)}}[\log p(X,Z|\theta)] - \mathbb{E}_{Q^{(t+1)}}[\log Q^{(t+1)}(Z)] \]

其中第二项与\(\theta\)无关，故M步等价于最大化期望完全数据对数似然：

\[\theta^{(t+1)} = \arg\max_\theta \mathbb{E}_{Q^{(t+1)}}[\log p(X,Z|\theta)] \]

4. 单调递增性证明

每次迭代后，新参数满足：

\[\begin{aligned} \log p(X|\theta^{(t+1)}) &\geq \mathcal{L}(Q^{(t+1)},\theta^{(t+1)}) \\ &\geq \mathcal{L}(Q^{(t+1)},\theta^{(t)}) \\ &= \log p(X|\theta^{(t)}) \end{aligned} \]

因此，对数似然函数在每次迭代后非减，保证收敛到局部极大值。

Parametric estimate

一种简单的想法是规定 Hawkes Process 里面的核函数，如经典的

\[g(t)= \alpha \omega e^{-\omega t} \\ g(t)=\frac{\alpha}{(t+\omega)^{\eta+1}} \]

规定完函数之后，假设我们已经有了若干组发生过的数据，我们可以用MLE或者EM取估计这些参数。

我们以 \(g(t)= \alpha \omega e^{-\omega t}\)为例。

\[\lambda(t)=\mu+\sum_{t_i<t} \alpha\omega e^{-\omega (t-t_i)} \]

如果我们有一组 \([0,T]\) 的数据，Point Process 为 \(\{t_i\}_{i=1}^n\) ,则似然函数是：

\[l(\Theta)=\sum_{i=1}^n \log(\lambda(t_i))-\int_{0}^T \lambda(t)dt \]

如果我们直接使用MLE，可以得到三个偏微分方程，但他们显然是超越方程组。

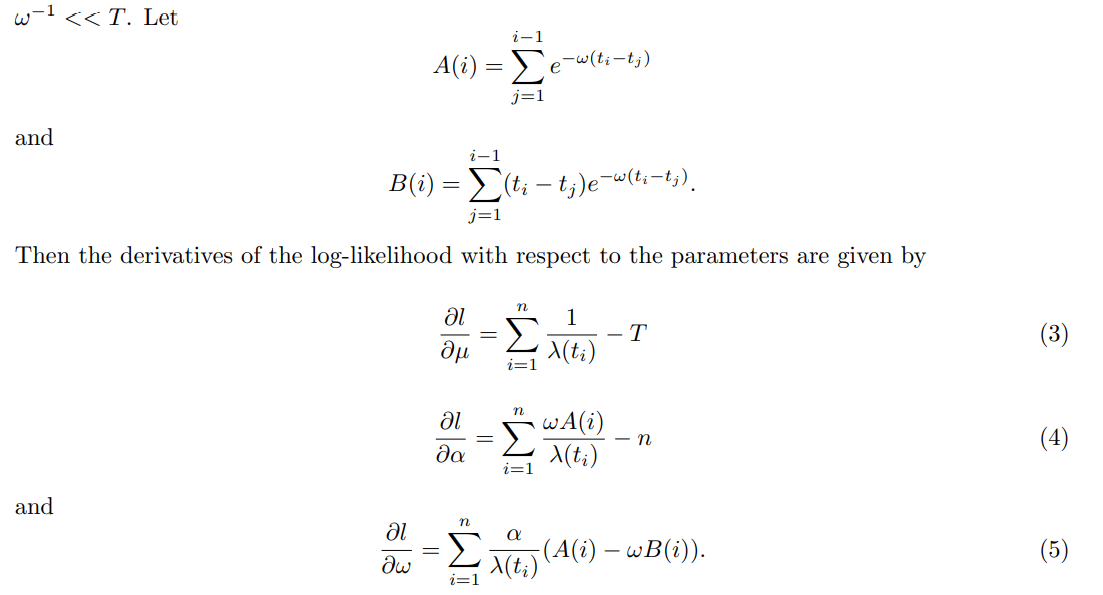
这三个方程组可以得到解析解。但是算法不会实现，所以要通过以下的 EM 算法来找出数值解。

让 \(p_{ij}\) 代表事件 \(i\) 引起事件 \(j\) 的概率 ，\(p_{ii}\) 是 \(i\) 引发自己的概率。则显然 \(p_{ij}\) 是一组隐变量， E-step 容易得到：

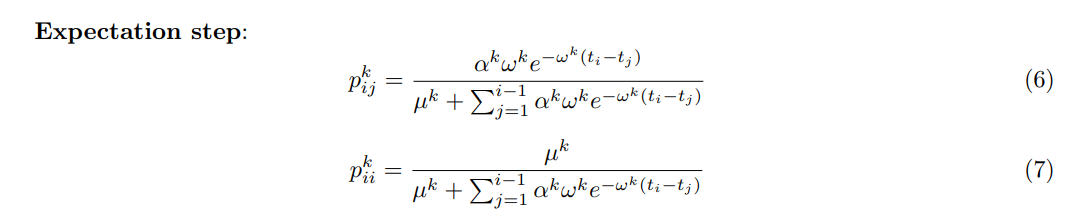
重点是 M-step，我们该如何构建一个似然函数，用上 \(p_{ij}\)

\[Q=\log p(X,Z|\theta)=\sum_{i=1}^n[\log \mu \cdot p_{ii} +\sum_{j=1}^{i-1}(\log(\alpha\omega)-\omega(t_i-t_j))]-\int_{0}^T (\mu+\sum_{t_j<t}\alpha\omega e^{-\omega(t-t_j)}) dt \]

求三个偏微分，解方程即可得到

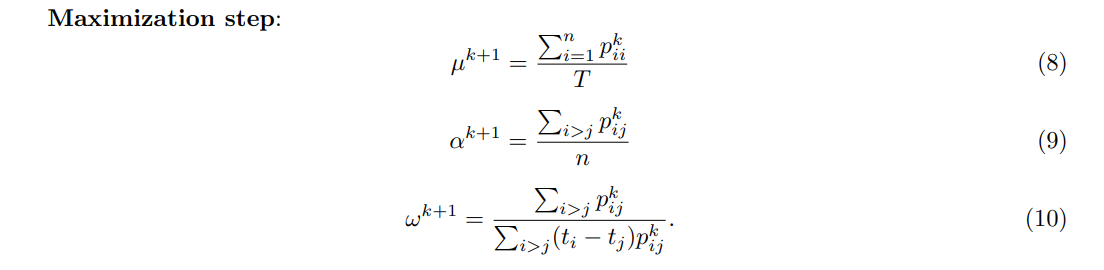
迭代过程本质是梯度下降，满足

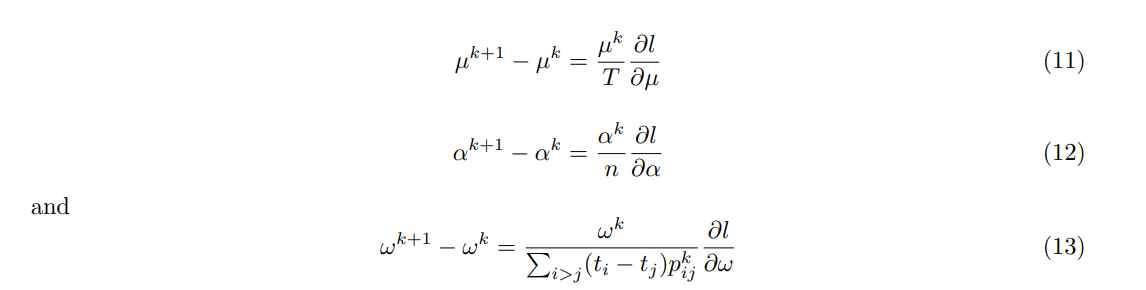
Non Parametric estimate

直接给定 kernal 的形式还是有一定的局限性。

固有了非参数估计的 Hawkes Process，他的核心做法是：

1. kernal 函数不是提前给定，而是从 \(L^1(\mathbb R)\) 中选取任意多个组合。（实现时可以选取一个基函数集合）
2. 离散化时间窗口，通过变分法转化为 Euler-Lagrange 方程组从而转化为 ODE 问题再求解出 kernal 函数。

同理，引入隐变量

展开对数似然函数

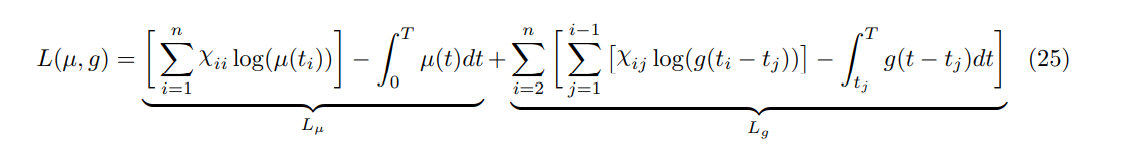
现在，我们的隐变量仍然是 \(p_{ij}\) ,但参变量变成了 \(\mu(t),g(t)\) 这两个函数而不是 \(\alpha, \mu, \omega\) 这三个数字。

E-step 没有什么变化

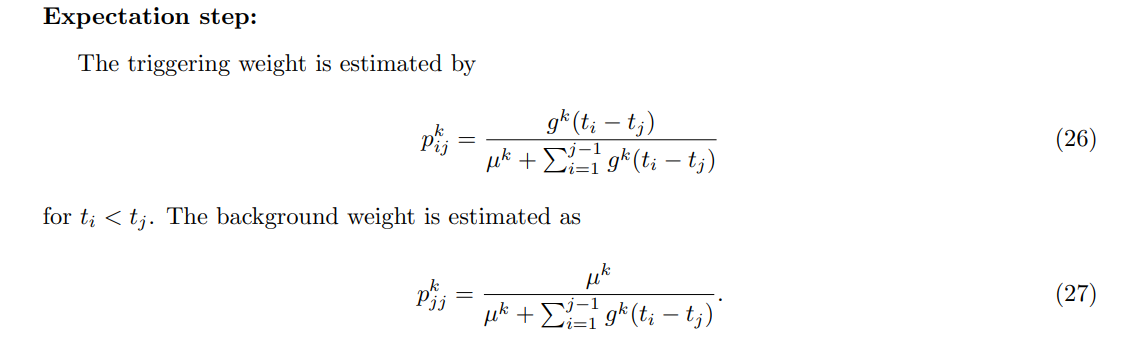
M-step，由于似然函数 \(L(\mu,g)\) 拆成了独立的两部分 \(L_{\mu}+L_g\) ,故可以分别求解。

变分法 & Euler-Lagrange 方程

泛函：从一个函数映射到一个数

问题：现在有一个积分泛函 \(J(y)=\int_{a}^b F(x,y,y_x) dx, y\) 在 \([a,b]\) 上二阶可微，为了让泛函取极大/小值， \(y(x)\) 应当满足什么条件

结论： $$\frac{\partial F}{\partial y} - \frac{d}{dx}(\frac{\partial F}{\partial y_x}) = 0$$

证明：设 \(J(y)\) 取极值的时候，\(y=u(x)\) , 则设 \(y(x)=u(x)+\varepsilon \eta(x)\) , \(\varepsilon\) 是一个实数， \(\eta(x)\) 是任意一个其他的函数，并且其一旦确定， \(y\) 只与 \(\varepsilon\) 有关。

任取一个 \(\eta(x), J(y)=J(u+\varepsilon \eta)=J(\varepsilon)\)

且一定满足 \(\frac{dJ(\varepsilon )}{d \varepsilon }_{|\varepsilon =0}=0\) 因为 \(\varepsilon =0\) 时 \(y=u\)

\(\eta(a)=\eta(b)=0\) 是因为 \(y\) 和 \(u\) 在起点和终点的值一定是相等的。

泛函导数

上述式子只能求解形式固定的表达式，对于一般的表达式并不是很方便，介绍一种好用的方法，泛函导数。

那其实就是把这个函数看成一个自变量正常去微分和求导就行了。

再来看本题的两个方程，他们是类似的，这里解决较为复杂的 \(g\).

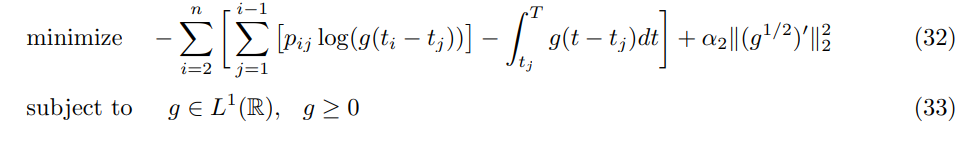
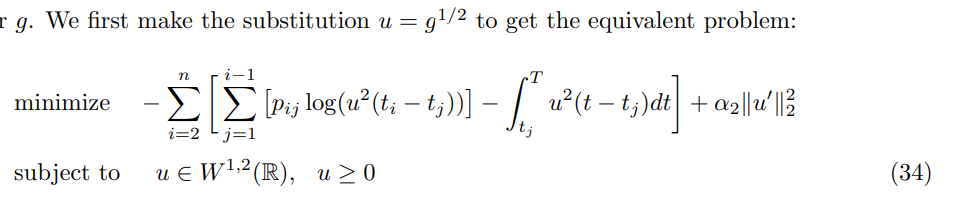
（注意这里只是单纯设 \(u=g^{1/2}\) ,并不是上面的 \(u\)；正则项前面是负号，原文有点问题）

​目标函数标准化

原始目标函数：

\[\begin{aligned} \mathcal{J}[u] = &-2 \sum_{i=2}^{n} \sum_{j=1}^{i-1} p_{ij} \log u(t_i - t_j) \\ &+\sum_{j=1}^{n} \int_{t_j}^{T} u^2(t-t_j) dt \\ &- \alpha_2 \int_{0}^{T} (u'(t))^2 dt \end{aligned} \]

通过变量替换 $ s = t - t_j $，积分项改写为：

\[\sum_{j=1}^{n} \int_{t_j}^{T} u^2(t-t_j) dt=\sum_{j=1}^n \int_{0}^{T-t_j} u^2(s) ds \]

3. 分项计算变分导数

定义：

• $ D(t) = \sum_{i,j} p_{ij} \delta(t - (t_i - t_j)) $
• $ C(t) = \sum_j \Theta((T - t_j) - t) $

其中:

这个Dirac函数是转化为积分的常用手法

对 $ u(t) $ 施加扰动 $ \delta u(t) $，计算各部分泛函导数：

​(1) 对数项的变分

\[\begin{aligned} \delta \left(-2 \sum_{i,j} p_{ij} \log u\right) &= -2 \sum_{i,j} p_{ij} \frac{\delta u(t_i - t_j)}{u(t_i - t_j)} \\ &= -2 \int_0^T \frac{\sum p_{ij} \delta(t - (t_i - t_j))}{u(t)} \delta u(t) dt \\ &= -2 \int_0^T \frac{D(t)}{u(t)} \delta u(t) dt \end{aligned} \]

​(2) 积分项的变分

\[\begin{aligned} \delta \left(\sum_j \int_0^{T-t_j} u^2 ds\right) &= 2 \sum_j \int_0^{T-t_j} u \delta u \, ds \\ &= 2 \int_0^{T} \left( \sum_j \Theta((T - t_j) - t) \right) u(t) \delta u(t) dt \\ &= 2 \int_0^T C(t) u(t) \delta u(t) dt \end{aligned} \]

​(3) 正则化项的变分

\[\begin{aligned} \delta \left(-\alpha_2 \int_0^T (u')^2 dt\right) &= -2\alpha_2 \int u' \delta u' dt \\ &= -2\alpha_2 \int u'' \delta u dt \end{aligned} \]

分部积分，边界项为零

​总变分方程

将三部分变分合并：

\[\int_{0}^{T} \left[ -2 \frac{D(t)}{u(t)} + 2 C(t) u(t) - 2 \alpha_2 u''(t) \right] \delta u(t) dt = 0 \]

​欧拉-拉格朗日方程

消去公共因子 $ 2 $，调整符号后：

\[\boxed{ -\alpha_2 u''(t) + C(t) u(t) = \frac{D(t)}{u(t)} } \]

一个简单的实现方式是切成若干段，转连续为离散.

\[\boxed{ -\alpha_2 \frac{u_{m+1}-2u_m+u_{m-1}}{(\delta t)^2} + C_m u_m = \frac{D_m}{u_m} } \]

其中 \(C_m= \sum_{i:T-t_i<m\delta t} 1, D_m=\frac{1}{\delta t} \sum_{i,j} p_{i,j}[m \delta t<t_i-t_j<(m+1)\delta t]\)

这个东西是一个二次方程组，用 Seidel type iterative method 即可。