多校冲刺 NOIP2021 (17) —「宝藏·寻找道路·猪国杀·数树」

宝藏

\(nlog^2n\) 的做法就是对每个数二分他最多能覆盖到哪个询问。
\(nlogn\) 的做法，就是利用宝藏多中位数不增的性质，单调指针扫，可以少一个 \(log\) , 要想维护可以用主席树或者权值线段树。

寻找道路

我感觉挺 \(NB\) 的题，但是大佬们都考场切了。

一个切入点就是最终答案不取模数会很大，所以要想比大小不太现实，也就是最短路应该舍弃，所以考虑类似 \(bfs\) 的东西。

首先可以把和1连边为0的点缩成一个团，那么到每个点，距离最短是优先的。
同时要保证字典序最小，考虑 \(zfs\) ( ZZ_zuozhe 优化的 bfs ，简称zfs（ZZ_zuozhe first search））。

zfs可以用来处理字典序问题，思路就是时刻保证队列里面 ZZ优先 按字典序排序。
由于字典序扩展具有单调性，\(zfs\) 的 \(bfs\) 性质保证了二段性，所以可以这么做，但是需要保证字典序单调扩展。
保证的方法就是每次取出队列中字典序相同的所有元素，先扩展0在扩展1。
可以扩展到更高的进制，复杂度为 \(O(kn)\) , k是进制数。

猪国杀

颓题解颓了半天才明白的NB计数题，但被沈（神）队称为“完全就是个套路题”。

首选有概率期望的线性性展开，就是把矩形颠倒一下，这个确实是套路。
假设 \(g_x\) 为恰好选择 \(x\) 张牌时候的方案数，那么，答案可以被轻松表示成 \(\sum\limits_{x=0}^{n} g_x*x\)
假设 \(f_x\) 为选择\(\geq x\) 张牌时候的方案数，那么，答案可以被转化成 \(\sum\limits_{x=0}^{n} f_x\)

原理就是这个，（偷的大佬的图），第一种方式是每次竖着统计，第二种方式是每次横着统计。

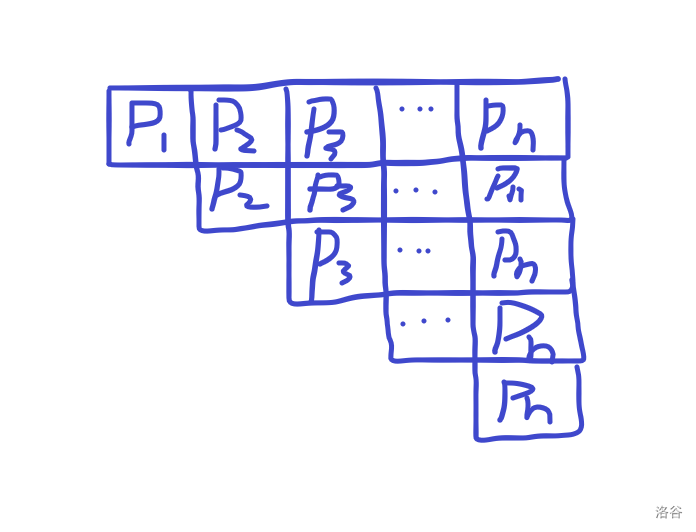
然后考虑计算 \(f_x\) ，首先根据选最多牌的策略，选出来的序列肯定是单调不降的。
由于将题意转化成选 \(\geq x\) 张牌，所以我们只需要保证至少选择了 \(x\) 张牌，并且方案不会重复，就可以统计到答案里面。

计算 \(f_x\) 的过程，可以考虑固定 \(x\) 张小于最大值的牌，然后选若干张最大值（俺想不出来，沈队说直接想）
设 \(g_{i,j,k}\) 代表选了 \(i\) 张牌，每张都 \(\leq j\) ，总和 \(\leq k\) 的方案数。
那么，\(f_x=\sum\limits_{j=1}^{A}\sum\limits_{k=1}^{n-x}\binom{n}{x}*g_{x,j-1,m-j*x}*(\sum_{t\geq k}\binom{n-x}{t}*(A-j)^{n-x-t})\)
\(x\) 就是小于最大值的选择了几张，然后\(j\) 枚举最大值，\(k\) 枚举选择了几张最大值，\(t\) 枚举有几张最大值，剩下的随便选。

注意这里还有一个问题就是这样统计会导致最终我们选完 \(x+k\) 张牌之后，可能还能再选别的牌。
但是这并不重要，因为，我们只需要保证至少选择了 \(x\) 张牌。

注意这里为了避免排列统计重复，有一个需要注意的就是必须确定最大值选择了几张。

换句话说，就是原式子的最后一部分 \((\sum_{t\geq k}\binom{n-x}{t}*(A-j)^{n-x-t})\) ，不能写成 \((\binom{n-x}{k}*(A-j+1)^{n-x-k})\)

举例来说明一下，我们需要统计有 \(3\) 个数，至少有一个 \(1\) 的排列，手模一下就会发现，由于我们乘了组合数的原因，会算重。

然后考虑 \(g\) 怎么算，显然可以背包计算（ \(1e8\) ），但是有容斥方法。

设\(h_{i,j,k}\) 代表至少有 \(i\) 张 \(>j\) ，总和 \(\leq k\) 的方案数，那么答案可以写成 \(\sum\limits_{t=0}^i(-1)^t*\binom{i}{t}*h_{t,j,k}\)

0这个是二项式反演 \(m=0\) 的情况，其实退化成普通容斥了，只需要计算 \(h\) 就行了。

\(h_{i,j,k}=\binom{k-i*(j+1)+i}{i}\) 上面是先钦定选不合法再插板，因为可以插空板所以还要加 \(i\) 。

这个插空版小于等于是个套路，挺NB的。

下面选 \(i\) 而不是 \(i-1\) 的原因是让 \(\sum \leq k\) ，还可以插一个板代表剩下的那部分不用了。
计算 \(g\) 的过程及时 \(break\) , 复杂度是调和级数，\((\sum_{t\geq k}\binom{n-x}{t}*(A-j)^{n-x-t})\) 可以用扫描线优化计算。

复杂度 \(O(n^2mlogm)\) 。

数树

仙姑

总结

这场打的非常sb。

开场先浏览题，T1一堆单调性感觉想想复杂度就对了，T2 DAG很好做，然后就想缩点，T3，T4一眼没啥思路，估计最后只有暴力。
所以给我自己的期望是 100+100+暴力+暴力。

T1想了半个小时就会一个log了，但是不知道为什么状态不好调了2h，直接心态崩了，导致后面低错频繁。
T2以为能开bitset，然后就搞了个缩点+拓扑，点内最短路，点外拓扑。

但是我当时状态不好，根本就不能用bitset存，并且我当时一会认为自己方法是正解，一会hack，浪费了很多时间，最后暴力都没码完。
其实如果打完T1即使调整心态，就可以100+50+20+40，虽然不高但也不至于垫底。

感觉这场的上限是100+100+20+40，仔细分析T2的条件最后想bfs也不是很困难，就是T1花了很多时间然后就爆炸了。

还有就是其实思维僵化了，见到有向图就想缩点，其实直接最短路、bfs就行（还有不得不吐槽老爱想tarjan，tarjan打不对真是个sb。

这场T1打完没有调整心态而是慌慌忙忙去做T2是很失误的决策，T2没想明白复杂度就码也很不对，本质是慌了，以后要避免。