「联赛复习」——图论
由于一些模版当初学的时候很懵逼,所以来填坑。
学习的时候可能有不属于图论的额外收货,一并写下了。
extra—— 查看程序运行空间
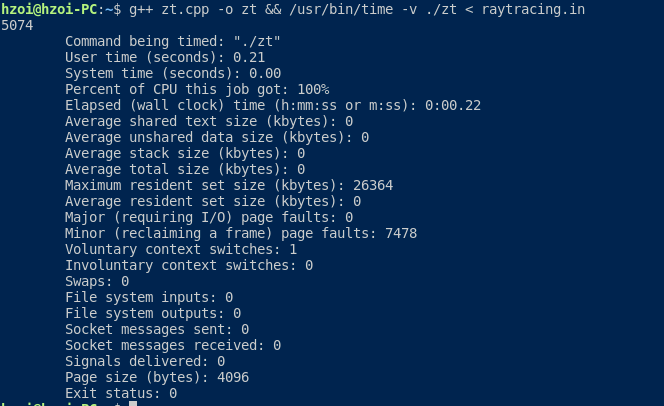
发现有一个nb操作可以直接输出你程序的使用空间(包括vector的,和系统栈空间)
/usr/bin/time -v 代替 time ,效果如下。
Maximum resident set size 就是空间,除1024换算到 \(MB\),这个不爆应该就不会爆。
Prim算法
当初觉得这玩意没用然而在一次长了教训,但是之后又不太会了。
主要用于稠密的一批的图( \(n^2 \sim m\) )求最小生成树。
思想类似于Djkla,维护两个集合,一个是已经确定最小距离的,一个是未确定的。
时刻维护未确定的到确定的最小距离,每次选最小的扩展,和克鲁一样基于贪心。
引用以下大佬的话。
证明:Prim算法之所以是正确的,主要基于一个判断:对于任意一个顶点v,连接到该顶点的所有边中的一条最短边(v, vj)必然属于最小生成树(即任意一个属于最小生成树的连通子图,从外部连接到该连通子图的所有边中的一条最短边必然属于最小生成树)
次小生成树
不知道这个东西能出出来什么不是模版的题。
思路很简单,对于每条非树边,加到树上必定形成一个环。
非树边的权值必定大于等于所有树边权值。
所以只要能知道树上路径的最小值和次小值就行了。
可以倍增实现,注意初始化的时候 \(dis2=Inf\) ,因为一开始没有次小的边。
转移分类讨论就行了,感觉次小的都是这个分类讨论的套路,详见蓝书 P385;
次短路
和上面那个一样, \(Dij\) 的时候把次短的扔进去让他们松弛就好了。
扔个模版跑路。
memset( dis1 , 0x3f , sizeof( dis1 ) ) , memset( dis2 , 0x3f , sizeof( dis2 ) ) ;
dis1 [1] = 0 , q.push( mp( 0 , 1 ) ) ;
while( !q.empty() ){
int x = q.top().second , ww = q.top().first ; q.pop() ;
for( R i = head [x] ; ~i ; i = net [i] ){
int y = to [i] ;
if( dis1 [y] > ww + w [i] ){
dis2 [y] = dis1 [y] ;
dis1 [y] = ww + w [i] ;
q.push( mp( dis1 [y] , y ) ) , q.push( mp( dis2 [y] , y ) ) ;
} else if( dis1 [y] != ww + w [i] && dis2 [y] > ww + w [i] ){
dis2 [y] = ww + w [i] ;
q.push( mp( dis2 [y] , y ) ) ;
}
}
} printf( "%d\n" , dis2 [n] ) ;
传递闭包
布尔弗洛伊德,处理连通性问题和信息传递,可以 \(bitset\) 优化到 \(n^3/w\)
就一个式子 f[i][j]|=(f[i][k]&f[k][j]) , bitset优化后 if(f[i][k])f[i]|=f[k]。
和弗洛伊德一样的枚举分界点+dp的思想。
欧拉路,欧拉回路
分有向图和无向图,先说判定条件。
有向图,回路 入度=出度
有向图,路径 入度=出度 ,但存在两个特殊点 一个入度=出度-1,一个出度=入度-1
无向图,回路 每个点度为偶数
无向图,路径 每个点度为偶数,可以存在两个点度为奇数。
注意递归层数是 \(O(m)\) 的所以最好手写栈否则会很慢,注意是每个点递归完的时候入栈。
放一个模版
void dfs( int x ){
st [++ top] = x ;
while( top ){
int x = st [top] , i = head [x] ;
if( ~i ){
int y = to [i] ;
if( vis [i] ) continue ;
vis [i] = 1 , st [++ top] = y , head [x] = net [i] ;
} else ans [++ ans [0]] = x , top -- ;
}
}
例题 , 很容易想到一个哈密顿回路做法,就是把每个点向能连的连边,最后要求通过所有点。
但是通过所有点的回路是 \(Np\) 的,这种情况需要考虑把信息转移到边上 ,每个点是 m-1 位数,每个边是0/1,求欧拉回路就行了。
有的时候让输出最小字典序,拍一下序就行了,当然如果你不懂怎么排序,由于他是回路,所以我们找到这个串的最小表示法就行了。
最小表示法,就是时刻维护两个指针指可能的最小串。
先把串原样复制一遍到后面,主要思想就是 \([i,i+k]<[j,j+k]\) ,那么, \([j,j+k]\) 每个点都不可能成为最小表示法开头。
放个模版跑路
R i = 1 , j = 2 , k , ans ;
while( i <= n && j <= n ){
for( k = 0 ; k < n && s [i + k] == s [j + k] ; k ++ ) ;
if( k == n ) break ; assert( s [i + k] != s [j + k] ) ;
if( s [i + k] > s [j + k] ) i += k + 1 , i += ( i == j ) ;
else j += k + 1 , j += ( i == j ) ;
} ans = min( i , j ) ;
for( R i = ans , j = 1 ; j <= n ; j ++ , i ++ ) printf( "%d " , s [i] ) ;
Tarjan
超级大坑,好不容易填坑。
有向图强连通分量,缩点
先搞出来原图的一颗 dfs 树,则有以下四类边
树边,前向边,返祖边,横叉边。
返祖边和横叉边可能出环,所以在 \(dfs\) 的时候开一个栈保存所有可能出环的节点(其实到下文就知道这些就是遍历过且未被弹出的;
定义一个 \(low_x\) 代表以下节点时间戳最小值
- X子树内的点。
- X的子树指向的点。
转移根据实际意义,若是子树就 \(low\) 取min,若不是且在栈中就取 \(dfn\) 的min,本质是每次在这个点计算第二类点的贡献。
如果发现一个点 \(low_x==dfn_x\) , 那么说明他不能与栈中点构成环了,所以弹出统计就好了。
在计算 \(low\) 的时候我有时会忘记判断 \(in_stack\) , 一定要注意啦。
然后是缩点,正常缩就行了,注意有的时候可能要判断重边,缩完之后是一个 DAG ,这是一个很好的性质。
放一个模版,跑路了。
void tarjan( int x ){
low [x] = dfn [x] = ++ knt , ins [x] = 1 , st [++ top] = x ;
for( R i = head [x] ; ~i ; i = net [i] ){
int y = to [i] ;
if( !dfn [y] ){
tarjan( y ) , low [x] = min( low [x] , low [y] ) ;
} else if( ins [y] ) low [x] = min( low [x] , dfn [y] ) ;
} if( low [x] == dfn [x] ){
rnt ++ ; int z ;
do{
z = st [top --] ;
num [rnt] ++ ;
bel [z] = rnt ;
ins [z] = 0 ;
} while( z != x ) ;
}
}
// in main
for( R i = 1 ; i <= n ; i ++ ) if( !dfn [i] ) tarjan( i ) ;
for( R i = 2 ; i <= cnt ; i ++ ){
x = bel [fr [i]] , y = bel [to [i]] ;
if( x != y && p.find( mp( x , y ) ) == p.end() ) v [x].push_back( y ) , p [mp( x , y )] = 1 , dr [y] ++ ;
}
无向图 割点,桥
和有向图一样定义 \(low,dfn\) , 不难推出来判断条件。
一条边是割边,仅当存在 \(dfn_x<low_y\) 。
一个点是割点,仅当存在 \(dfn_x<=low_y\) , 如果是根要注意至少有两个点满足,因为只有一个点删掉它之后剩下的也联通。
多一个等号是因为就算到他这出环也没事因为要把他删掉。
计算割边要防止回搜,但是为了保全重边,所以用 xor 来做,割点就没这个问题因为相等也没事。
这个不用开栈,因为并没有缩点操作。
无向图点双,边双,缩点
边双:边双联通分量,不存在桥,删掉任意一条边仍然联通,任意两点之间有两条 边不重复路径
点双:点双联通分量,可以存在割点,但删掉任意一个点仍然联通,是特殊的边双,任意两点之间有两条 点不重复路径
其实有一种类似 电压机制 的边上差分求法,但是感觉信息不如 \(Tarjan\) 多。
求边双可以先求出来所有桥然后不让走桥划分联通块,然后可以缩点,缩完点就是一个树。
可以利用这个树解决无向图必经边的问题(s->t路径上的必经边)。
必经边代码
#include <bits/stdc++.h>
#define R register int
#define scanf Ruusupuu = scanf
#define freopen rsp_5u = freopen
#define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
int Ruusupuu ;
FILE * rsp_5u ;
using namespace std ;
typedef long long L ;
const int N = 1e5 + 10 ;
const int M = 4e5 + 10 ;
inline int read(){
int w = 0 ; bool fg = 0 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) fg |= ( ch == '-' ) , ch = getchar() ;
while( ch >= '0' && ch <= '9' ) w = ( w << 1 ) + ( w << 3 ) + ( ch ^ 48 ) , ch = getchar() ;
return fg ? -w : w ;
}
vector< int > v [N] ;
int n , m , x , y , head [N] , dfn [N] , low [N] , bge [M] , col [N] , rnt , q ;
int dep [N] , top [N] , sz [N] , bs [N] , fa [N] , knt ;
int fr [M] , to [M] , net [M] , cnt = 1 ;
#define add( f , t ) fr [++ cnt] = f , to [cnt] = t , net [cnt] = head [f] , head [f] = cnt
void sc(){
n = read() , m = read() , memset( head , -1 , sizeof( head ) ) ;
for( R i = 1 ; i <= m ; i ++ ) x = read() , y = read() , add( x , y ) , add( y , x ) ;
}
void dfs1( int x , int ed ){
dfn [x] = low [x] = ++ knt ;
for( R i = head [x] ; ~i ; i = net [i] ){
int y = to [i] ;
if( !dfn [y] ){
dfs1( y , i ) , low [x] = min( low [x] , low [y] ) ;
if( low [y] > dfn [x] ) bge [i] = bge [i ^ 1] = 1 ;
} else if( i != ( ed ^ 1) ) low [x] = min( low [x] , dfn [y] ) ;
}
}
void dfs2( int x ){
col [x] = rnt ;
for( R i = head [x] ; ~i ; i = net [i] ){
int y = to [i] ;
if( col [y] || bge [i] ) continue ;
dfs2( y ) ;
}
}
void dfs3( int x , int Fa ){
for( auto y : v [x] ){
if( y == Fa ) continue ;
fa [y] = x , dep [y] = dep [x] + 1 ;
dfs3( y , x ) , sz [x] += sz [y] ;
if( sz [y] > sz [bs [x]] ) bs [x] = y ;
} sz [x] ++ ;
}
void dfs4( int x , int tops ){
top [x] = tops ; if( !bs [x] ) return ;
dfs4( bs [x] , tops ) ;
for( auto y : v [x] ){
if( y == fa [x] || y == bs [x] ) continue ;
dfs4( y , y ) ;
}
}
inline int LCA( int x , int y ){
while( top [x] != top [y] ){
if( dep [top [x]] < dep [top [y]] ) swap( x , y ) ;
x = fa [top [x]] ;
} return ( dep [x] < dep [y] ) ? x : y ;
}
void work(){
dfs1( 1 , 0 ) ;
for( R i = 1 ; i <= n ; i ++ ) if( !col [i] ) ++ rnt , dfs2( i ) ;
for( R i = 2 ; i <= cnt ; i += 2 ) if( col [fr [i]] != col [to [i]] ) v [col [fr [i]]].push_back( col [to [i]] ) , v [col [to [i]]].push_back( col [fr [i]] ) ;
dfs3( 1 , 0 ) , dfs4( 1 , 1 ) , q = read() ; while( q -- ){
x = col [read()] , y = col [read()] ;
int lca = LCA( x , y ) ;
printf( "%d\n" , dep [x] + dep [y] - 2 * dep [lca] ) ;
}
}
signed main(){ // fre(in);
sc() ;
work() ;
return 0 ;
}
点双求的时候就不像边双那么简单了,还需要维护一个栈,只要满足割点判定法则都要进行一次点双的计算。
直接放一个无向图必经点的计算,我是弄了个圆方树,其实就是点双缩完之后的东西。
把每个割点看成一个点,每个点双看成一个点,若点双包含这个割点就连边。
主要就是每当满足判断条件就判点双,所以搞点双在遍历过程中完成。
code
#include <bits/stdc++.h>
#define R register int
#define scanf Ruusupuu = scanf
#define freopen rsp_5u = freopen
#define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
int Ruusupuu ;
FILE * rsp_5u ;
using namespace std ;
typedef long long L ;
const int N = 4e5 + 10 ;
const int M = 1e6 + 10 ;
inline int read(){
int w = 0 ; bool fg = 0 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) fg |= ( ch == '-' ) , ch = getchar() ;
while( ch >= '0' && ch <= '9' ) w = ( w << 1 ) + ( w << 3 ) + ( ch ^ 48 ) , ch = getchar() ;
return fg ? -w : w ;
}
vector< int > vcc [N] , v [N] ;
int n , x , y , dfn [N] , low [N] , knt , rnt , bel [N] , cut [N] , st [N] , top , root = 1 , num [N] , rl [N] ;
int fr [M] , to [M] , net [M] , head [N] , cnt = 1 , fa [N] ;
#define add( f , t ) fr [++ cnt] = f , to [cnt] = t , net [cnt] = head [f] , head [f] = cnt
void sc(){
n = read() , memset( head , -1 , sizeof( head ) ) ;
while( 98 ){
x = read() , y = read() ;
if( x == y && x == 0 ) break ;
add( x , y ) , add( y , x ) ;
}
}
void dfs1( int x ){
int fl = 0 ; st [++ top] = x ;
dfn [x] = low [x] = ++ knt ;
for( R i = head [x] ; ~i ; i = net [i] ){
int y = to [i] ;
if( !dfn [y] ){
dfs1( y ) , low [x] = min( low [x] , low [y] ) ;
if( low [y] >= dfn [x] ){
fl ++ , rnt ++ ;
if( fl > 1 || x != root ) cut [x] = 1 ;
int z ;
do{
z = st [top --] ;
vcc [rnt].push_back( z ) ;
} while( z != y ) ;
vcc [rnt].push_back( x ) ;
}
} else low [x] = min( low [x] , dfn [y] ) ;
}
}
void dfs2( int x , int Fa ){
for( auto y : v [x] ){
if( y == Fa ) continue ;
fa [y] = x ; dfs2 ( y , x ) ;
}
}
void work(){
dfs1( 1 ) , root = rnt ;
for( R i = 1 ; i <= n ; i ++ ) if( cut [i] ) num [i] = ++ root ;
for( R i = 1 ; i <= rnt ; i ++ ) for( auto j : vcc [i] ) ///printf( "%d %d\n" , i , j ) ;
if( cut [j] ) v [num [j]].push_back( i ) , v [i].push_back( num [j] ) , bel [j] = num [j] , rl [num [j]] = j ;
else assert( !bel [j] ) , bel [j] = i ;
x = read() , y = read() ;
if( x == y ) puts( "No solution" ) , exit( 0 ) ;
assert( bel [x] && bel [y] ) ;
// printf( "%d %d\n" , bel [x] , bel [y] ) ;
dfs2( bel [x] , 0 ) , y = bel [y] ;
int ans = 1e9 + 98 ;
while( y != bel [x] ){
if( cut [rl [y]] ) ans = min( ans , rl [y] ) ; y = fa [y] ;
} if( ans != 1e9 + 98 ) printf( "%d\n" , ans ) ; else puts( "No solution" ) ;
}
signed main(){ // fre(in);
sc() ;
work() ;
return 0 ;
}
二分图染色判定
性质:一张图不存在奇环 充要 这张图是二分图
因为每一条边都是从一个集合走到另一个集合,只有走偶数次才可能回到同一个集合。
所以可以染色判定。
建出补图缩完点之后,根据点双性质可以证明若一个点双内存在一个奇环,则所有点在奇环上。
证明利用了 奇数=奇数+偶数 的巧妙性质和一个点到一个环必定有两条路径。
所以只需要找到一个奇环就可以判断他不是二分图了,可以染色。
抄一下蓝书的伪代码
void dfs( int x , int color )
v [x] = color
for( y link to x )
if( !v [y] ) dfs( y , 3-color ) ;
else if( v [y] == color ) 不是二分图
// in main
for( i : 1->n) if(!v [i]) dfs(i,1);
放一下这题代码
code
#include <bits/stdc++.h>
#define R register int
#define scanf Ruusupuu = scanf
#define freopen rsp_5u = freopen
#define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
int Ruusupuu ;
FILE * rsp_5u ;
using namespace std ;
typedef long long L ;
const int N = 1e3 + 10 ;
const int M = 2e6 + 10 ;
inline int read(){
int w = 0 ; bool fg = 0 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) fg |= ( ch == '-' ) , ch = getchar() ;
while( ch >= '0' && ch <= '9' ) w = ( w << 1 ) + ( w << 3 ) + ( ch ^ 48 ) , ch = getchar() ;
return fg ? -w : w ;
}
vector< int > vcc [N] ;
int n , m , x , y , knt , rnt , dfn [N] , low [N] , fg [N] , st [N] , top , root , win , a [N][N] ;
int fr [M] , to [M] , net [M] , head [N] , cnt = 1 , col [N] , bel [N] ;
#define add( f , t ) fr [++ cnt] = f , to [cnt] = t , net [cnt] = head [f] , head [f] = cnt
void tarjan( int x ){
low [x] = dfn [x] = ++ knt , st [++ top] = x ;
for( R i = head [x] ; ~i ; i = net [i] ){
int y = to [i] ; //printf( "%d %d\n" , x , y ) ;
if( !dfn [y] ){
tarjan( y ) , low [x] = min( low [x] , low [y] ) ;
if( low [y] >= dfn [x] ){
rnt ++ ; int z ;
do{
z = st [top --] ;
vcc [rnt].push_back( z ) ;
} while( z != y ) ;
vcc [rnt].push_back( x ) ;
}
} else low [x] = min( low [x] , dfn [y] ) ;
}
}
void dfs( int x , int color , int bels ){
col [x] = color ;
for( R i = head [x] ; ~i ; i = net [i] ){
int y = to [i] ; if( bel [y] != bels ) continue ;
if( !col [y] ) dfs( y , 3 - color , bels ) ;
else if( col [y] == color ) win = 0 ;
}
}
inline bool check( int x ){
win = 1 ;
for( auto j : vcc [x] ) col [j] = 0 , bel [j] = x ;
for( auto j : vcc [x] ) if( col [j] == 0 ) dfs( j , 1 , x ) ;
return !win ;
}
void work(){
while( 98 ){
for( R i = 2 ; i <= cnt ; i ++ ) net [i] = 0 ;
for( R i = 1 ; i <= rnt ; i ++ ) vcc [i].clear() ;
n = read() , m = read() ;
for( R i = 1 ; i <= n ; i ++ ) head [i] = -1 , fg [i] = 0 , dfn [i] = low [i] = bel [i] = col [i] = 0 ;// memset( head , -1 , sizeof( head ) ) ,
for( R i = 1 ; i <= n ; i ++ ) for( R j = 1 ; j <= n ; j ++ ) a [i][j] = 0 ;
if( !n && !m ) break ;
cnt = 1 , knt = rnt = top = 0 ;
for( R i = 1 ; i <= m ; i ++ ) x = read() , y = read() , a [x][y] = a [y][x] = 1 ;
for( R i = 1 ; i <= n ; i ++ ) a [i][i] = 1 ;
for( R i = 1 ; i <= n ; i ++ ) for( R j = 1 ; j <= n ; j ++ ) if( !a [i][j] ) add( i , j ) ;
for( R i = 1 ; i <= n ; i ++ ) if( !dfn [i] ) root = i , tarjan( i ) ;
for( R i = 1 ; i <= rnt ; i ++ ) if( check( i ) ) for( auto j : vcc [i] ) fg [j] = 1 ;
int ans = 0 ; for( R i = 1 ; i <= n ; i ++ ) ans += ( fg [i] == 0 ) ;//, printf( "%d\n" , fg [i] ) ;
printf( "%d\n" , ans ) ;
}
}
signed main(){ // fre(y);
work() ;
return 0 ;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号