dp优化—斜率优化+凸优化
好了不做大鸽子了更个大个的博。
前言
本来想写点前言划会水,但是发现不知道写啥。
斜率优化
之前学的时候还挺明白的,但是长时间不学就忘记了,正好之前也只会单调队列的斜率优化。
代数法和几何法各有优势,几何法个人感觉比较好用。
只需要拆出来只和 \(i\) 有关的,只和 \(j\) 有关的,和 \(i,j\) 乘积项有关的,和他们都无关的。
随意一题为例子(博主太懒直接搬运了)
这种情况下 只与 \(j\) 有关和常数当成 \(y\) , 只与 \(i\) 有关(尤其要包含 \(dp_i\) )当成 \(b\) , \(i,j\) 乘积项中的 \(i\) 有关当成 \(x\) , \(j\) 有关当成 \(k\) 。
然后对于每个决策点 \(i\) , 他决策的过程就是去之前的 \((x,y)\) 的点集中寻找最优决策点的过程,斜率优化的本质就是及时排除不可能的决策点。
如上,化成这个样子之后会有一下几种情况
一:k,x均单调
这样我们直接单调建凸包单调弹队头就可以了,使用单调队列维护。
二:x单调,k不单调
这样我们可以单调建凸包,求值的时候去二分当前斜率能切到哪个点(mid和mid+1形成的直线比斜率)
三:x,k均不单调
可以选择 \(cdq\) 分治,流程如下。
- cdq分治之前,把所有点按k排序,进入cdq分治。
- 如果l==r,直接返回,否则重复3-7。
- 进行归并排序的逆过程,让 \([l,mid]\) , \([mid+1,r]\) 内的点分别按k排序,并且保证左边的点id<=mid
- 递归求解 \([l,mid]\) ,并保证递归结束后 \([l,mid]\) 内的点按 x 有序。
- 左边点已经按 x 有序,我们可以单调的建凸包,右边的点已经按 k 有序,我们可以单调的弹队头。
- 递归解决 \([mid+1,r]\) ,并保证递归结束后 \([mid+1,r]\) 内的点按 x 有序
- \([l,mid],[mid+1,r]\) 的点已经分别按 x 有序 , 归并排序使得 \([l,r]\) 内的点按 x 有序。
这里给出模版题 building bridges 的实现代码。
code
#include <bits/stdc++.h>
#define int long long
#define R register int
#define scanf Ruusupuu = scanf
#define freopen rsp_5u = freopen
#define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
int Ruusupuu ;
FILE * rsp_5u ;
using namespace std ;
typedef long long L ;
typedef double D ;
const int N = 1e5 + 10 ;
const int Inf = 1e18 + 98 ;
inline int read(){
int w = 0 ; bool fg = 0 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) fg |= ( ch == '-' ) , ch = getchar() ;
while( ch >= '0' && ch <= '9' ) w = ( w << 1 ) + ( w << 3 ) + ( ch ^ 48 ) , ch = getchar() ;
return fg ? -w : w ;
}
int n , h [N] , w [N] , sum [N] , f [N] , q [N] ;
struct T{ int id , k , x , y ; } t [N] , z [N] ;
inline bool cmp( T a , T b ){ return a.k < b.k ; }
inline bool czp( T a , T b ){ return a.x < b.x ; }
inline double slope( int x , int y ){
if( t [x].x == t [y].x ) return ( t [x].y > t [y].y ) ? -Inf : Inf ;
return ( 1.0 * t [y].y - 1.0 * t [x].y ) / ( 1.0 * t [y].x - 1.0 * t [x].x ) ;
}
void sc(){
n = read() ;
for( R i = 1 ; i <= n ; i ++ ) h [i] = read() , t [i].id = i , t [i].k = ( h [i] << 1 ) , t [i].x = h [i] ;
for( R i = 1 ; i <= n ; i ++ ) w [i] = read() , sum [i] = sum [i - 1] + w [i] ;
sort( t + 1 , t + 1 + n , cmp ) ;
}
void cdq( int l , int r ){
if( l == r ) return t [l].y = f [t [l].id] - sum [t [l].id] + h [t [l].id] * h [t [l].id] , void() ;
int mid = ( l + r ) >> 1 , p1 = l , p2 = mid + 1 , hh = 1 , tt = 0 ;
for( R i = l ; i <= r ; i ++ ) ( t [i].id <= mid ) ? z [p1 ++] = t [i] : z [p2 ++] = t [i] ;
assert( p1 == mid + 1 && p2 == r + 1 ) ;
for( R i = l ; i <= r ; i ++ ) t [i] = z [i] ;
cdq( l , mid ) ;
for( R i = l ; i <= mid ; i ++ ){
while( hh < tt && slope( q [tt - 1] , q [tt] ) >= slope( q [tt - 1] , i ) ) tt -- ;
q [++ tt] = i ;
} for( R i = mid + 1 ; i <= r ; i ++ ){
while( hh < tt && slope( q [hh] , q [hh + 1] ) <= t [i].k ) hh ++ ;
if( hh <= tt ){
int zt = q [hh] ;
f [t [i].id] = min( f [t [i].id] , f [t [zt].id] + sum [t [i].id - 1] - sum [t [zt].id] + ( h [t [i].id] - h [t [zt].id] ) * ( h [t [i].id] - h [t [zt].id] ) ) ;
}
} cdq( mid + 1 , r ) ;
p1 = l , p2 = mid + 1 ;
for( R i = l ; i <= r ; i ++ ){
if( p1 == mid + 1 ) z [i] = t [p2 ++] ;
else if( p2 == r + 1 ) z [i] = t [p1 ++] ;
else ( t [p1].x < t [p2].x ) ? z [i] = t [p1 ++] : z [i] = t [p2 ++] ;
} for( R i = l ; i <= r ; i ++ ) t [i] = z [i] ;
}
void work(){
memset( f , 0x3f , sizeof( f ) ) , f [1] = 0 , cdq( 1 , n ) ;
printf( "%lld\n" , f [n] ) ;
}
signed main(){
// fre(in) ;
sc() ;
work() ;
return 0 ;
}
校内题:打怪 link
由邻项交换法可以证明如果没有秒杀操作,按 \(\frac{c}{a}\) (c是击杀所用次数)排序是最优的。
所以先按那个排一下序,并且如果可以计算在秒杀第 \(i\) 只怪的情况下秒杀哪只怪最优,就可以得到答案了。
可以写出来表达式,然后发现也是斜率优化的模型,就是 \(k,x\) 都不单调。
四:炒鸡大杀器
其实以上操作均可以用李超线段树完成(三种情况都可以,复杂度为 \(nlogW\)), \(W\) 是值域。
对于第三种情况来说,转移需要保证 \(j\leq i\) , 所以在 \(j\) 的时候把对应的 \(k\) 丢进李超线段树就行了。
但是需要注意一个问题,就是这种做法的时空复杂度都是 \(nlogW\) 的,有时候 \(W\) 很大可能会导致空间复杂度无法接受。
加上 cdq 代码难度并不大,所以还是推荐用以上三种做法。
所以你以为李超线段树就是一个空间复杂度大的 fw ?大错特错。
先简单介绍一下,李超线段树是一个支持区间取 \(max\) 一次函数的一种线段树,是对线段树的一种变形。
他是靠维护这个区间最具有优势的直线/线段+标记永久化实现的,具体不再介绍。
插入一条直线的复杂度是 \(logW\) , 插入一条线段的复杂度是 \(log^2 W\) 。
在偏序只有一维的时候(转移只需要满足 \(j\leq i\) ),可以从前往后插直线,一个log
当偏序有多维的时候,可以任意顺序插线段,两个log
所以先来看一道斜率优化直接做很麻烦的题 :擒敌拳
转移方程是这样的 \(f_i=max(f_j+(i-l_j+1)*h_j),r_j\geq i\) , 发现不仅要满足偏序,k,x还不单调。
这种情况,你当然可以通过cdq套set维护凸包解决,或者线段树凸包解决。
但是直接李超树就很简单的,建出笛卡尔树之后直接在每个节点插入一条线段,斜率为 \(h_x\) , 截距为 \(( 1 - l_x ) * h [x]\) 的线段。
当前线段的左右端点是 \([x,r_x]\) , 然后直接在每个点查询就行了。
这个东西除了辅助斜率优化还有其他用途,比如维护区间取 \(max\) 一次函数,区间查询函数最值
比如 游戏 ,代码我没有写,因为就是李超+树剖,不过这题是区间查询。
区间查询其实标记永久化也是可以做的,这个等复习标记永久化,线段树合并的时候再说吧。
这里还有一道李超树合并模版题,link , 没码,复习的时候再说吧。
凸优化
这是当 \((j,f_j)\) 在坐标系上形成的点是凸\凹函数的时候可以考虑的优化方式
这里学的不是很深,因为感觉暂时不是很重要。
这里咕了好多题没有做,到时候再说吧,加括号是我做过的,有幸联赛不退役再来填坑吧(大概率永远鸽掉)。
wqs二分
我啥也没写,要学主要看论文。
题:忘情,林克卡特树,邮局,CF 739E , 征途 ,(ABC218H)。
只是很浅的学习了一下,就是在要求恰好选择多少个物品的时候计算代价的一种方式。
斜率切凸包的方式没怎么理解,就是在让所有物品都减少一个价值,然后看会取到多少个,当恰好取到需要的个数的时候再把减掉的加回来就行了。
放一个模版(ABC218H),就是记录当前代价最多最小选多少个,希望我下次看代码能理解。
code
#include <bits/stdc++.h>
#define int long long
#define R register int
#define scanf Ruusupuu = scanf
#define freopen rsp_5u = freopen
#define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)
int Ruusupuu ;
FILE * rsp_5u ;
using namespace std ;
typedef long long L ;
typedef double D ;
const int N = 2e5 + 10 ;
const int Inf = 1e10 + 98 ;
inline int read(){
int w = 0 ; bool fg = 0 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) fg |= ( ch == '-' ) , ch = getchar() ;
while( ch >= '0' && ch <= '9' ) w = ( w << 1 ) + ( w << 3 ) + ( ch ^ 48 ) , ch = getchar() ;
return fg ? -w : w ;
}
int n , r , a [N] ;
struct ZT{
int val , mi , mx ; ZT(){}
ZT( int _v , int _i , int _x ){ val = _v , mi = _i , mx = _x ; }
inline friend ZT max( ZT a , ZT b ){
if( a.val != b.val ) return a.val > b.val ? a : b ;
else return ZT( a.val , min( a.mi , b.mi ) , max( a.mx , b.mx ) ) ;
} inline friend ZT operator + ( ZT a , int b ){ return ZT( a.val + b , a.mi , a.mx ) ; }
} f [N][2] ;
void sc(){
n = read() , r = read() ;
for( R i = 1 ; i < n ; i ++ ) a [i] = read() ;
}
inline ZT calc( int x ){
memset( f , 0 , sizeof( f ) ) ;
for( R i = 1 ; i <= n ; i ++ ){
f [i][0] = max( f [i - 1][1] + a [i - 1] , f [i - 1][0] ) ;
f [i][1] = max( f [i - 1][0] + a [i - 1] , f [i - 1][1] ) ;
f [i][1].mx ++ , f [i][1].mi ++ , f [i][1].val -= x ;
} return max( f [n][0] , f [n][1] ) ;
}
void work(){
int lside= -Inf , rside = Inf , ans ;
while( lside <= rside ){
int mid = ( lside + rside ) >> 1 ;
ZT zt = calc( mid ) ;
// printf( "%lld %lld %lld %lld\n" , mid , zt.val , zt.mi , zt.mx ) ;
if( zt.mx < r ) rside = mid - 1 ;
else if( zt.mi > r ) lside = mid + 1 ;
else{ ans = zt.val + mid * r ; break ; }
} printf( "%lld\n" , ans ) ;
}
signed main(){ // freopen("fake.in","r",stdin),freopen("fake.out","w",stdout);
sc() ;
work() ;
return 0 ;
}
max\min 卷积,闵可夫斯基和
题:(ABC218H)(假人),穿越时空,bzoj3252攻略
这种题就当函数是凸的的时候 \(n^2\) 转移的时候用的,分治+闵可夫斯基和,因为是凸的所以差分表单调,每次贪心的选择大的差分就行了。
对于假人那道题其实是 ABC218H 的加强版,因为只有在 mod 12 的意义下第二维才有凸性。
提醒我们 实在找不到凸性可以分开找有凸性的部分。
slope trick
题: EP219,CF1534G,烟火表演,agc49E,(CF713C),(ABC217H)
这种题就当函数是凸的时候 \(n*W\) 转移的时候用的,\(W\) 是值域,本质是维护的拐点集合,每个拐点斜率增加一。
一般形式是维护左右两个堆分别存斜率大于0和小于0的部分,左右top之间的连线斜率为0 。
注意必须所有斜率都是整数的时候才可以使用,统计答案的过程比较优美,在每次都统计斜率为0的线的纵坐标变化量。


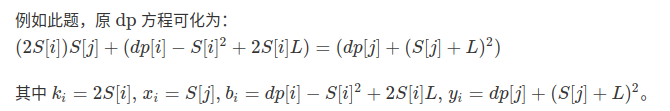

 浙公网安备 33010602011771号
浙公网安备 33010602011771号