模拟24—「matrix·block·graph」
matrix
考试的时候直接暴力枚举了,其实想了想分行枚举,但是没有继续下去。
先说一下标准的分行枚举
就是记录这行的选择状态和上一行的选择状态,转移的时候枚举上一行的上一行就能填表转移,枚举下一行可以填表转移。
这样是 $ O(2^{3m})$的复杂度,无法通过 $ m \leq 10 $ 。
所以他来减少状态数量 —— 让一个状态是另一个状态的子集
这个要是直接想到的话不是很难,通过优化的套路想到也不是不可能。
只要我们能让枚举一个状态是另一个状态的子集,那么枚举这两维状态的复杂度就由 \(O(n2^{2m})\)到了 \(O(n3^m)\) , 这是可以通过二项式定理证明的。
证明:\(2^n\)个数的数的所有子集一共有 \(3^n\) 个
字面理解组合数就行了。
所以我们只需要枚举上一行的覆盖状态和他的子集,选择状态,就可以把时间复杂度降到了 \(O(n*2^m*3^m)\) ,就能通过了。
这里注意一个细节,如果我们选择填表转移,那么我们无法快速剪枝,只有到了枚举出来上一行的选择状态才能剪枝,但是如果我们枚举本行的状态进行填表,那么我们可以在枚举下一行之前进行剪枝。
对于这类循环多的题,可以想想什么样的循环顺序可以更好的剪枝,从而进行优化提高运行效率。
还有就是能预处理出来就只算一边预处理出来,尤其是那么 \(lowbit\) ,不要让他跑很多次,也是费时间的。
还有,状压一定要加括号!!
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <bitset>
#include <iostream>
#include <vector>
#define R register int
#define int long
#define printf Ruusupuu = printf
#define scanf Ruusupuu = scanf
#define freopen rsp_5u = freopen
int Ruusupuu ;
FILE * rsp_5u ;
using namespace std ;
typedef long long L ;
typedef double D ;
const int N = 2e1 ;
const int Inf = 0x3f3f3f3f ;
inline void of(){ freopen( "in.in" , "r" , stdin ) , freopen( "out.out" , "w" , stdout ) ; }
inline void cf(){ fclose( stdin ) , fclose( stdout ) ; }
inline int read(){
int w = 0 ; bool fg = 0 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) fg |= ( ch == '-' ) , ch = getchar() ;
while( ch >= '0' && ch <= '9' ) w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) , ch = getchar() ;
return fg ? -w : w ;
}
int n , m , ans = Inf , cost [N][N] , cst [11][1 << 11] , w [1 << 11][N] , lg [1 << 20] , f [11][1 << 11][1 << 11] , beg [N] ;
char s [N][N] ;
int sub [1 << 11][1 << 11] ;
#define lb( x ) ( x & (-x) )
inline void debug( int x ) { cout << bitset<10>(x) << endl ; }
void sc(){
n = read() , m = read() ;//, p = n * m ;
for( R i = 1 ; i <= n ; i ++ ){
scanf( "%s" , s [i] + 1 ) ;
int len = strlen( s [i] + 1 ) ;
for( R j = 1 ; j <= len ; j ++ )
beg [i] |= ( ( s [i][j] - '0' ) << ( j - 1 ) ) ;
}
for( R i = 1 ; i <= n ; i ++ )
for( R j = 1 ; j <= m ; j ++ )
cost [i][j] = read() ;
}
//卡常经历:能预处理出来的不要每次都lowbit重新算一次。我以前一直以为lowbit算算挺快的,没想到这么费
void work(){
lg [0] = -1 ; for( R i = 1 ; i <= ( 1 << m ) ; i ++ ) lg [i] = lg [i / 2] + 1 ;
for( R i = 0 ; i < ( 1 << m ) ; i ++ )
for( R j = 0 ; j < ( 1 << m ) ; j ++ )
if( ( i & j ) == j ) //枚举子集一定要加括号,显着没事就要加括号!!!淦淦淦
sub [i][++ sub [i][0]] = j ;
for( R j = 1 ; j <= n ; j ++ ){
for( R i = 0 ; i < ( 1 << m ) ; i ++ ){
R u = i ;
while( u ){
w [i][lg [lb( u )]] = 1 , cst [j][i] += cost [j][lg [lb( u )] + 1] ;
u -= lb( u ) ;
}
}
}
for( R i = 1 ; i <= n ; i ++ ) memset( f [i] , 0x3f , sizeof( f [i] ) ) ;
for( R i = 1 ; i <= n ; i ++ ){ //枚举行
for( R j = 0 ; j < ( 1 << m ) ; j ++ ){ // 这一行的选择状态
R r = j ;
r |= ( j << 1 ) , r |= ( j >> 1 ) ;
r |= beg [i] ;
r &= ( ( 1 << m ) - 1 ) ;
if( i == 1 ){ f [1][j][r] = cst [i][j] ; continue ; }
for( R k = 0 ; k < ( 1 << m ) ; k ++ ){ //上一行的覆盖状态
for( R x = 1 ; x <= sub [k][0] ; x ++ ){ // 枚举子集——选择状态
int l = sub [k][x] ;
if( f [i - 1][l][k] == Inf ) continue ;
R q = r | l ;
f [i][j][q] = min( f [i][j][q] , f [i - 1][l][k] + cst [i][j] ) ;
}
}
}
}
int ans = 0x3f3f3f3f ;
for( R i = 0 ; i < ( 1 << m ) ; i ++ )
ans = min( ans , f [n][i][( 1 << m ) - 1] ) ;
printf( "%ld\n" , ans ) ;
}
signed main(){
// of() ;
sc() ;
work() ;
// cf() ;
return 0 ;
}
block
一开始以为是 \(dp\) ,但是死活都推不出来式子,感觉有可能是排序一下贪心,但是一下没啥思路,所以就只打了个暴力。
正解很恶心,俺根本想不到。
考虑 \(n!\) 种排列方式除了把 \(12345\) 这种序列全排列还有什么产生方式。
如果我们把 \(n\) 个数按次序加入序列,并且保证加入每个数的=时候他都可以放在任意一个位置,那么,放置第一个数的时候有 \(1\) 种方案,第二个数有两种,以此类推。
当我们把这些数都加入这个序列后,会发现我们一共有 \(n!\) 种方式把这些数加入序列,分别对应了 $n! $ 种全排列。
这为我们求排列数量提供了一种思路:不考虑处理全排列,而是考虑添加数的过程,看每一次有多少种方案把这个数加进去。
回到本题,如果按上述思路考虑,那么我们只需要先给序列进行排序,保证 \(val\) 大的在前面,这样,加入一个 \(<key,val>\) 时,假设他是第 \(k\) 个加入的,那么他加入的方案就有 \(min(k,key)\) 种。
因为我们排完序,导致他加入的时候序列里面的数必定都比他小,排序是为了消除后效性,因为这样后面的数就不会对他造成影响,换句话说,所有能对他造成影响的数已经被加到序列中了,那么每个数在此时能对答案贡献多少,他最终就能对答案贡献多少。
但是我们发现可能有 \(val\) 相同的情况,这样我们需要 按照 \(key\) 为第二关键字从小到大排序,因为 \(key\) 更大,所以不能让小 \(k\) 给祸害掉,也就是他可能还有更多的可能放到这个序列中。
这提示我们 \(min(k,key)\) 也需要修改了,因为有重复的 \(val\) ,所以加入序列时,除了大于他的,还有等于他的,而等于他的并不占用 \(key\) ,所以我们需要记录一下有多少个等于他的,然后用 \(min(key+same,i)\) 来更新答案。
那么第一问就完了。
第二问就按题目说的做就行了,我们按照 \(key,val\) 为第一二关键字从小到大排序,能选择序列最前面的一个数,我们就选择序列最前面的数,选择他之后 \(val\) 比他小的数的 \(key\) 要减去1,不能选择序列最前面的数,当且仅当有其他数的 \(key=1\),这代表我们必须选择他。
\(n^2\) 模拟出来上述过程之后发现可以用线段树优化,只不过每次更新看一看是否有点 \(key=1\) ,如果有就把它更新成答案。
code
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <bitset>
#include <iostream>
#include <vector>
#include <assert.h>
#define R register int
#define int long
#define printf Ruusupuu = printf
#define scanf Ruusupuu = scanf
#define freopen rsp_5u = freopen
int Ruusupuu ;
FILE * rsp_5u ;
using namespace std ;
typedef long long L ;
typedef double D ;
const int N = 5e5 + 10 ;
const int Inf = 0x3f3f3f3f ;
const int P = 1e9 + 7 ;
inline void of(){ freopen( "in.in" , "r" , stdin ) , freopen( "out.out" , "w" , stdout ) ; }
inline void cf(){ fclose( stdin ) , fclose( stdout ) ; }
inline int read(){
int w = 0 ; bool fg = 0 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) fg |= ( ch == '-' ) , ch = getchar() ;
while( ch >= '0' && ch <= '9' ) w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) , ch = getchar() ;
return fg ? -w : w ;
}
int n , ans = 1 , res [N] ;
struct T{ int key , val , id ; } a [N] , b [N] , c [N] ;
inline bool cmp( T a , T b ){ return ( a.val == b.val ) ? ( a.key < b.key ) : ( a.val > b.val ) ; }
inline bool csp( T a , T b ){ return ( a.val == b.val ) ? ( a.key < b.key ) : ( a.val < b.val ) ; }
inline void T( int &a , int b ){ a = ( 1ll * a * b ) % P ; }
void sc(){
n = read() ;
for( R i = 1 ; i <= n ; i ++ ) a [i].key = b [i].key = c [i].key = read() , a [i].val = b [i].val = c [i].val = read() , a [i].id = i ;
}
struct Ts{ int l , r , minkey , pos , tkey , lz ; } t [N << 2] ;
int pos , dlt , lx , rx ;
inline void ud( int x ){
t [x].minkey = min( t [x << 1].minkey , t [x << 1 | 1].minkey ) ;
t [x].tkey = min( t [x << 1].tkey , t [x << 1 | 1].tkey ) ;
t [x].pos = ( t [x << 1].minkey <= t [x << 1 | 1].minkey ) ? ( t [x << 1].pos ) : ( t [x << 1 | 1].pos ) ;
if( t [x << 1 | 1].tkey == 1 ) t [x].minkey = t [x].tkey = 1 , t [x].pos = t [x << 1 | 1].pos ;
if( t [x << 1].tkey == 1 ) t [x].minkey = t [x].tkey = 1 , t [x].pos = t [x << 1].pos ;
}
void sp( int x ){
if( !t [x].lz ) return ;
int k = t [x].lz ; t [x].lz = 0 ;
t [x << 1].lz += k , t [x << 1 | 1].lz += k ;
t [x << 1].tkey -= k , t [x << 1 | 1].tkey -= k ;
}
void build( int x , int l , int r ){
t [x].l = l , t [x].r = r ;
if( l == r ) return t [x].minkey = t [x].tkey = a [t [x].l].key , t [x].pos = l , void() ;
int mid = ( l + r ) >> 1 ;
build( x << 1 , l , mid ) ;
build( x << 1 | 1 , mid + 1 , r ) ;
ud( x ) ;
}
void update( int x ){
if( t [x].l == t [x].r ) return t [x].minkey = t [x].tkey = Inf , void() ;
sp( x ) ; int mid = ( t [x].l + t [x].r ) >> 1 ;
if( pos <= mid ) update( x << 1 ) ;
else update( x << 1 | 1 ) ;
ud( x ) ;
}
void tothend( int x ){
if( t [x].l == t [x].r ) return ;
sp( x ) ;
if( t [x << 1].tkey == 1 ) tothend( x << 1 ) ;
if( t [x << 1 | 1].tkey == 1 ) tothend( x << 1 | 1 ) ;
ud( x ) ;
}
void cge( int x ){
if( rx < lx ) return ;
if( t [x].l >= lx && t [x].r <= rx ){
t [x].tkey -- , t [x].lz ++ ;
if( t [x].tkey == 1 ) tothend( x ) ;
return ;
}
sp( x ) ; int mid = ( t [x].l + t [x].r ) >> 1 ;
if( lx <= mid ) cge( x << 1 ) ;
if( rx > mid ) cge( x << 1 | 1 ) ;
ud( x ) ;
}
inline void debug(){
for( R x = 1 ; x <= 4 * n ; x ++ ) printf( "%ld %ld %ld %ld %ld %ld\n" , t [x].l , t [x].r , t [x].minkey , t [x].tkey , t [x].pos , t [x].lz ) ;
}
void work(){
sort( a + 1 , a + 1 + n , cmp ) ;
int same = 0 ;
for( R i = 1 ; i <= n ; i ++ ){
if( a [i].val == a [i - 1].val ) same ++ ;
else same = 0 ;
T( ans , min( i , a [i].key + same ) ) ;
}
sort( a + 1 , a + 1 + n , csp ) ;
build( 1 , 1 , n ) ;
for( R i = 1 ; i <= n ; i ++ ){
res [i] = t [1].pos ;
pos = t [1].pos , update( 1 ) ;
lx = 1 , rx = pos - 1 , cge( 1 ) ;
}
printf( "%ld\n" , ans ) ;
for( R i = 1 ; i <= n ; i ++ ) printf( "%ld %ld\n" , a [res [i]].key , a [res [i]].val ) ;
}
signed main(){
// of() ;
sc() ;
work() ;
// cf() ;
return 0 ;
}
graph
又是一道好题。
我考场上的思路是对 \(-1\) 边造成影响的所有边进行离散化。
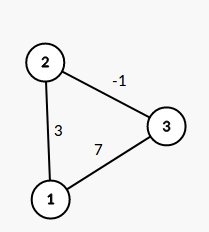
举个最简单的例子。
对于这张图,\(-1\) 能造成影响的就是 \(2->3\) 的路径,当其边权为 \(10\) 时对其有影响,还能对\(1->3\)的路径有影响,当其边权为\(4\)的时候。
也就是,我只把所有经过\(-1\)的三角(广义下的三角,并非三条边)搞出来,然后把其两边之和和差的绝对值存起来,以后搜索用。
这样,对每个存起来的值,跑一边 \(\mathrm{DIJ}\),判断路径上的点,我们只需要从 \(1\) 跑一遍,从 \(n\) 跑一遍,然后枚举点,看哪些点 \(dis [1][i] + dis [i][n] = dis [1][n]\) ,就证明他是最短路上的点。
上述可以拿到 \(60pts\) ,因为存起来的值到最后可能有 \(30W^+\) ,导致我们跑不完,我们最多跑 \(2000\) 次左右,所以我们 random_shuffle 一下,只搜前两千个,然后就能 \(AC\)
但是这种玄学做法,主要原因就是需要搜的东西太多了,有些搜到的还是没用。
但是DIJ判断点这个方法还是非常好的。
对于边权是x的边,设计一个dp状态,\(f_{i,j}\)代表从1到i的最短路上经过j条边的最短路。
二维spfa就可以解决这个dp。
我们一开始的时候默认-1的边权是0。
那么,如果当-1边取值为x的时候,那么经过k条边到达n的最短路就是\(kx+f_{n,k}\)
由于我们已经有了\(f_{n,k}\),所以,枚举每个k,解出来如果最终的最短路上经过了k条边,那么x的取值范围是多少。
如果是一个合法范围,直接带入跑一遍正反dij。
最终把所有的东西都或起来就是答案。
这个思路很清奇,从和我完全不同的角度思考了这个问题。
本质就是它利用了所有的-1边取值必须相同,所以只关心最短路上经过几条-1边,缩小了状态范围。
而我没有利用取值相同之一特点,导致状态数飙升。
当状态数不在可处理范围时,一般是通过观察或者推理性质来缩小状态范围。
code
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#define mp make_pair
#define R register int
#define int long long
#define printf Ruusupuu = printf
#define scanf Ruusupuu = scanf
#define freopen rsp_5u = freopen
int Ruusupuu ;
FILE * rsp_5u ;
using namespace std ;
typedef long long L ;
typedef double D ;
typedef pair< int , int > PI ;
const int N = 1e3 + 10 ;
const int M = 4e3 + 10 ;
const int Inf = 0x3f3f3f3f3f3f3f ;
inline void of(){ freopen( "in.in" , "r" , stdin ) , freopen( "out.out" , "w" , stdout ) ; }
inline void cf(){ fclose( stdin ) , fclose( stdout ) ; }
inline int read(){
int w = 0 ; bool fg = 0 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) fg |= ( ch == '-' ) , ch = getchar() ;
while( ch >= '0' && ch <= '9' ) w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) , ch = getchar() ;
return fg ? -w : w ;
}
int n , m , x , y , z , st [N] , top , dis [N][M >> 1] , nop ;
int fr [M] , to [M] , net [M] , head [N] , cnt = 1 ;
#define add( f , t ) fr [++ cnt] = f , to [cnt] = t , net [cnt] = head [f] , head [f] = cnt , w [cnt] = z
struct T{ int id , k ; T(){} T( int _id , int _k ){ id = _id , k = _k ; } } ;
bool vis [N][M >> 1] , kp [M] , res [N] , fg [N] ;
D Dis [N] , nz [N] , DIS [N] , w [M] ;
void sc(){
n = read() , m = read() , memset( head , -1 , sizeof( head ) ) ;
for( R i = 1 ; i <= m ; i ++ ){
x = read() , y = read() , z = read() ;
if( z == -1 ) z = 0 , st [++ top] = i , kp [i << 1] = kp [i << 1 | 1] = 1 ;
add( x , y ) , add( y , x ) ;
}
}
void spfa(){
queue< T > q ;
memset( dis , 0x3f , sizeof( dis ) ) ;
q.push( T( 1 , 0 ) ) , dis [1][0] = 0 , vis [1][0] = 1 ;
// for( R i = 1 ; i <= cnt ; i ++ ) printf( "%lld %lld %lld\n" , fr [i] , to [i] , w [i] ) ;
while( !q.empty() ){
T x = q.front() ; q.pop() , vis [x.id][x.k] = 0 ;
// printf( "%lld %lld\n" , x.id , x.k ) ;
for( R i = head [x.id] ; ~i ; i = net [i] ){
int y = to [i] ;
if( kp [i] ){
// printf( "%lld %lld %lld %lld\n" , dis [y][x.k + 1] , dis [x.id][x.k] , x.id , x.k ) ;
if( x.k < top && dis [y][x.k + 1] > dis [x.id][x.k] ){
dis [y][x.k + 1] = dis [x.id][x.k] ;
if( !vis [y][x.k + 1] ) vis [y][x.k + 1] = 1 , q.push( T( y , x.k + 1 ) ) ;
}
}
else{
if( dis [y][x.k] > dis [x.id][x.k] + w [i] ){
dis [y][x.k] = dis [x.id][x.k] + w [i] ;
if( !vis [y][x.k] ) vis [y][x.k] = 1 , q.push( T( y , x.k ) ) ;
}
}
}
}
// for( R i = 1 ; i <= n ; i ++ )
// for( R j = 0 ; j <= top ; j ++ )
// printf( "%lld %lld %lld\n" , i , j , dis [i][j] ) ;
}
inline void Run( D x ){
priority_queue< PI , vector< PI > , greater< PI > > q ;
for( R i = 1 ; i <= top ; i ++ ) w [st [i] << 1] = w [st [i] << 1 | 1] = x ;
for( R i = 1 ; i <= n ; i ++ ) Dis [i] = (D)Inf , fg [i] = 0 ;
Dis [1] = 0 , q.push( mp( 0 , 1 ) ) ;
while( !q.empty() ){
int x = q.top().second ; q.pop() ;
if( fg [x] ) continue ; fg [x] = 1 ;
for( R i = head [x] ; ~i ; i = net [i] ){
int y = to [i] ;
if( Dis [y] > Dis [x] + w [i] ){
Dis [y] = Dis [x] + w [i] ;
q.push( mp( Dis [y] , y ) ) ;
}
}
}
for( R i = 1 ; i <= n ; i ++ ) fg [i] = 0 , DIS [i] = (D)Inf ;
DIS [n] = 0 , q.push( mp( 0 , n ) ) ;
while( !q.empty() ){
int x = q.top().second ; q.pop() ;
if( fg [x] ) continue ; fg [x] = 1 ;
for( R i = head [x] ; ~i ; i = net [i] ){
int y = to [i] ;
if( DIS [y] > DIS [x] + w [i] ){
DIS [y] = DIS [x] + w [i] ;
q.push( mp( DIS [y] , y ) ) ;
}
}
}
for( R i = 1 ; i <= n ; i ++ )
res [i] |= ( Dis [i] + DIS [i] == Dis [n] ) ;
}
void work(){
spfa() ;
for( R i = 0 ; i <= top ; i ++ ){
D l = 0 , r = (D)Inf ;
for( R j = 0 ; j < i ; j ++ )
r = min( r , ( 0.0 + dis [n][j] - dis [n][i] ) / ( 0.0 + i - j ) ) ;
for( R j = i + 1 ; j <= top ; j ++ )
l = max( l , ( 0.0 + dis [n][j] - dis [n][i] ) / ( 0.0 + i - j ) ) ;
// printf( "LR%lf %lf\n" , l , r ) ;
if( l > r ) continue ;
else nz [++ nop] = l ;
}
for( R i = 1 ; i <= nop ; i ++ ) Run( nz [i] ) ;
for( R i = 1 ; i <= n ; i ++ ) printf( "%d" , res [i] ) ;
}
signed main(){
// of() ;
sc() ;
work() ;
// cf() ;
return 0 ;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号