线性筛及其扩展
本弱太弱了,大佬们都熟练掌握线性筛的用法,而当初学的时候我只会打一个板子,所以我来补补课。
前言
线性筛首先是线性的。
所以\(500ms\)可以过掉\(1e7\)。
其次线性筛可以做的不止求素数,他可以在线性时间内求出任何积性函数的值。
所以,当数据范围很大的时候(\(<=5e7\)),我们可以考虑看看要求的东西满不满足积性。
然后可以考虑用线性筛。
很重要的一个事情是线性筛里面每个数都是被最小质因子筛掉的。
利用这个性质,我们通过分类讨论枚举的数里面有没有这个质因子,进行计算。
同时,如果我们枚举的数里面有当前枚举到的质因子,接下来的数就不应该被这个这个数筛掉了。
因为接下来的数一定有更小的质因子。
举一个最简单的例子
我们在枚举\(6\),先用\(2\)筛掉了\(12\)。
这个时候,我们发现\(6\)里面有\(2\),所以就应该停。
因为接下来的数肯定最小质因子就是\(2\),而不是枚举的质数。
这里来几个线性求积性函数的例子,也是常见的积性函数。
upd 8.22
觉得之前写的东西太麻烦了,没有简洁突出重点,现在来更新一下。
积性函数
知道什么函数是积性函数也是有点用的。
虽然如果我们是在无法证明可以先调和求出来打个表观察他积不积性
从OI-wiki上抄点东西。
首先我们可以知道一些基本的积性函数
然后,如果一个函数是通过积性函数的一下变换得到的,那么他也是积性函数。
其中卷积很常用。
然后就是筛的问题了。
筛积性函数
这个东西一般不是太难,因为可以少考虑一种情况。
如果一个数是质数,我们一般可以直接推出来他的函数值是啥。
如果他被一个之前质因子没有的筛掉,直接用积性解决。
所以只需要考虑被之前有的质因子筛掉会怎样。
这个一般我们就对最小质因子动点手脚,开几个东西记录一下他的值。
很一般的思考方式就是把它算术唯一分解之后考虑每个质因子的贡献。
举几个例子。
筛约数个数
先拆成公式 \(\prod\limits_{i=1}^{cnt}(a_i+1)\) 。
然后就很简单了,只需要记录一下他的答案和他的最小质因子的贡献。
每次被已有的最小质因子筛的时候除一下乘一下更新最小质因子的贡献就行了。
筛约数和
先拆成公式 \(\prod\limits_{i=1}^{cnt}(\sum\limits_{j=0}^{a_i}p_i^j)\)
然后同样的套路,记录一下他的答案和他的最小质因子的贡献。
被更新就把原来的都成p_i然后在加一就完事了。
筛积性函数的还有好多题,不过大多套用套路就行了。
筛非积性函数
DZY 就是个好例子,这种东西我们一般抄全套家伙。
在这道题中,我们需要筛出来 \(T(x)\)
主要难点就在我们需要看一个数所有质因子的次数是否相同。
这个时候需要一个高端操作:记录一个数去掉最小质因子之后的数。
所以我们记录一下
last_i 表示i去掉最小质因子剩下的数
could_i 表示i是否所有质因子次数都相同
num_i 表示i的最小质因子的次数
如果一个数的last合法,并且这个数的最小质因子次数等于他的last的最小质因子次数。
那么这个数合法。
依据这个,我们就可以筛出来T(x)了。
这个技巧可能不止限于非积性函数,积性函数也可以用这个技巧,如果很难直接求的话。


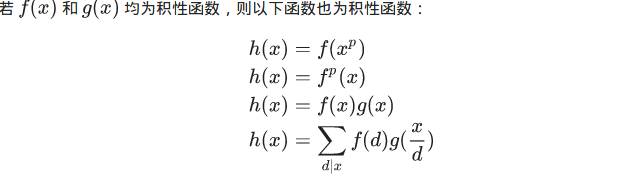

 浙公网安备 33010602011771号
浙公网安备 33010602011771号