星际旅行

题面大意是要求支持几种操作

• 查一个点到根节点的距离
• 给一个点的所有子数加一个值
• 断边，连边

保证是一棵树。

这个题好像是\(\mathtt {ETT}\)的模板题。

但是我懒得看，因为感觉动态树很高大上（主要是因为看不懂）。

同时由于太弱，一开始想拿\(dfs\)序做，后来发现儿子域挺不好维护的。

所以顺便结合网上资料学习了一下几种把树搞成序列的序，\(link\)

这道题使中，只需要使用一手欧拉序来维护。

所以查到根节点的距离，只需要查这个点的前缀和，入点加，出点减。
暂时认为这个方法没有问题，我们接着进行。

修改一个点的子树，因为有欧拉序，所以我们只需要给所有的入点加上一个值，所有的出点减去一个值就行了。
但是仔细撕烤，貌似有加有减不是很好搞啊。
所欲我们再开一个域，存他的符号
这样我们只需要把所有的绝对值加就行了，符号不用变。
然后搞一个区间修改就行了。

断边，连边这个操作，其实画画图就行了。
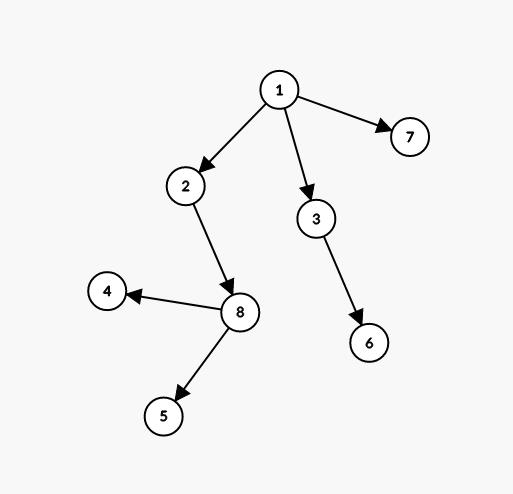
假设一开始，图是这样的

那么，他的欧拉序是1773663285544821
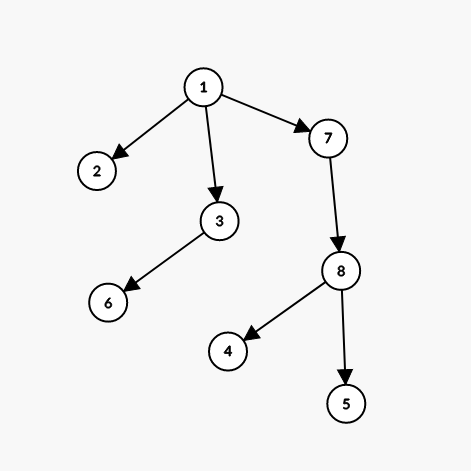
如果我们把8的父亲改成7,他变成了

他的欧拉序变成1785544873663221
可以发现就是把855448这个子树的欧拉序平移了而已。

理解也很好理解，一个子树用一个区间表示，把自己弄到别人区间，肯定是平移啊。

所以，我们只需要维护如下操作。

• 区间查询
• 区间修改
• 区间平移

查询和修改打一个标记就可以实现，但是这道题却加深了我对标记的理解。
和线段树中的标记一样，我们查询的时候，不一定所有标记都已经释放。
这就要求这我们修改一个点的时候，必须要把它的答案域也修改正确，而不能等待自然更新。

但是子树有正有负，怎么直接修改对答案呢?
想一想，如果是线段树的经典操作，我们就用他的子树中节点个数乘上要加的值就行了。
原理是每个节点都会贡献一个\(+1\)的系数。

在这道题中，有的点的贡献可能为负数，所以我们需要专门统计一下子数中对答案的贡献。
也就是，在本题中，需要开四个域来维护信息
分别是： 自己的值，自己的正负，子树的\(Sum_{val}\)，子树的\(Sum_{fuhao}\)

然后区间平移，需要一个操作—>提取区间
我们一开始先转出来要平移的区间，然后把他拿下来，然后在转出来被平移的入点的入点加一。
这个时候，入点和入点加一这个开区间内肯定是没有值的。
所以我们直接把它暴力插到\(ch[ch[root][1]][0]\)就行了。

但是你发现，如果转出来入点和加一，那么原来的区间就不在了。
这个时候，就需要这个操作了。

1. 把要提取的值设置成\(0\),然后向上传递一下信息，记录一下被删成\(0\)的节点编号，那么这个子数就从\(splay\)上面掉下来了。
2. 转出来需要的点，再把这个编号设置成他的子树，再向上更新一下，这个子树就又上去了。

有了这些操作，我们就不需要\(ETT\)了，可以通过。

code

#include <cstring>
#include <algorithm>
#include <cstdio>
#include <iostream>
#include <assert.h>
#define mp make_pair
#define R register int
#define int long long
#define scanf Ruusupuu = scanf
#define printf Ruusupuu = printf

int Ruusupuu ; 

using namespace std ;
typedef long long L ;
typedef long double D ;
typedef unsigned long long G ;
typedef pair< int , int > PI ;
const int N = 2e5 + 10 ;
const int Inf = 0x7fffffffff ;

inline int read(){	
	int w = 0 ; bool fg = 0 ; char ch = getchar() ;
	while( ch < '0' || ch > '9' ) fg |= ( ch == '-' ) , ch = getchar() ;
	while( ch >= '0' && ch <= '9' ) w = ( w << 1 ) + ( w << 3 ) + ( ch ^ '0' ) , ch = getchar() ;
	return fg ? -w : w ; 
}

int n , x , y , W [N] , m ; char bt [40] ;
int fr [N] , to [N] , head [N] , cnt = 1 , net [N] , top , st [N] , in [N] , out [N] ;
#define add( f , t ) fr [++ cnt] = f , to [cnt] = t , net [cnt] = head [f] , head [f] = cnt 
int root , znt , val [N] , son [N] , dis [N] , ch [N][2] , fa [N] , zf [N] , kl [N] , lz [N] , szf [N] ;

void sc(){
	n = read() , memset( head , -1 , sizeof( head ) ) ;
	for( R i = 2 ; i <= n ; i ++ ) x = read() , add( x , i ) ;
	for( R i = 1 ; i <= n ; i ++ ) W [i] = read() ;
}

#define sk( x ) ( x == ch [fa [x]][1] )
#define tr( x , dlt ) ch [x][dlt > val [x]]


inline void zt( int x ){
	if( !x ) return ;
	son [x] = son [ch [x][1]] + son [ch [x][0]] + 1 ;
	kl [x] = ( kl [ch [x][0]] + kl [ch [x][1]] + ( zf [x] * dis [x] ) ) ;
	szf [x] = ( szf [ch [x][0]] + szf [ch [x][1]] + zf [x] ) ;
}

inline void sp( int x ){ //下传的时候直接弄对答案域
	if( !lz [x] || !x ) return ;
	int k = lz [x] ; lz [x] = 0 ;
	if( ch [x][0] ) kl [ch [x][0]] += szf [ch [x][0]] * k , dis [ch [x][0]] += k , lz [ch [x][0]] += k ;
	if( ch [x][1] ) kl [ch [x][1]] += szf [ch [x][1]] * k , dis [ch [x][1]] += k , lz [ch [x][1]] += k ;
	zt( x ) ;
}

inline void spinup( int x ){
	R y = fa [x] , z = fa [y] , k = sk( x ) ;
	ch [z][sk(y)] = x , fa [x] = z ;
	ch [y][k] = ch [x][k ^ 1] , fa [ch [x][k ^ 1]] = y ;
	ch [x][k ^ 1] = y , fa [y] = x ; 
	zt( y ) , zt( x ) ;
}

void spall( int x ){ if( fa [x] != root && fa [x] != 0 ) spall( fa [x] ) ; sp( x ) ; }

inline void splay( int x , int pos ){
	spall( x ) ;
	while( fa [x] != pos ){
		R y = fa [x] , z = fa [y] ;
		if( z != pos ) sk( x ) ^ sk( y ) ? spinup( x ) : spinup( y ) ;
		spinup( x ) ; 
	} if( !pos ) root = x ;
}

inline void ins( int dlt , int ds , int zfs ){
	R now = root , fh = 0 ;
	while( now ) fh = now , now = tr( now , dlt ) ;
	now = ++ znt ;
	if( fh ) tr( fh , dlt ) = now ;
	val [now] = dlt , fa [now] = fh , dis [now] = ds , zf [now] = zfs , son [now] = 1 ;
	splay( now , 0 ) ; 	
}

inline int rk( int rank ){
	R now = root ;
	while( 1 ){
		sp( now ) ; R nxt = ch [now][0] ;
		if( son [nxt] + 1 < rank ) rank -= ( son [nxt] + 1 ) , now = ch [now][1] ;
		else if( son [nxt] >= rank ) now = nxt ;
		else { splay( now , 0 ) ; return now ; }
	}
}

inline int ngr( int x , bool fg ){
	splay( x , 0 ) ; 
	R now = ch [root][fg] ;
	while( ch [now][fg ^ 1] ) now = ch [now][fg ^ 1] ;
	return now ;
}

void dfs( int x ){
	st [++ top] = x , in [x] = top , ins( top , W [x] , 1 ) ;
	for( R i = head [x] ; ~i ; i = net [i] ) dfs( to [i] ) ;
	st [++ top] = x , out [x] = top , ins( top , W [x] , -1 ) ;
}

inline void Ask(){
	int pre = 2 * n + 1 , nxt = ngr( in [x] , 1 ) ;
	splay( pre , 0 ) , splay( nxt , pre ) ;
	printf( "%lld\n" , kl [ch [nxt][0]] ) ; 
}

inline void Cge(){
	int pre = ngr( in [x] , 0 ) , nxt = ngr( out [x] , 1 ) ;
	splay( pre , 0 ) , splay( nxt , pre ) ;
	int onnea = ch [nxt][0] ;
	kl [onnea] += szf [onnea] * y , dis [onnea] += y , lz [onnea] += y ; //直接更新答案域
	splay( onnea , 0 ) ; 	
}

inline void Azt(){
	int pre = ngr( in [x] , 0 ) , nxt = ngr( out [x] , 1 ) ;
	splay( pre , 0 ) , splay( nxt , pre ) ;
	int onnea = ch [nxt][0] ; ch [nxt][0] = 0 , fa [onnea] = 0 ;
	zt( nxt ) , zt( root ) ;
	
	
	pre = in [y] , nxt = ngr( in [y] , 1 ) ;
	splay( pre , 0 ) , splay( nxt , pre ) ;
	ch [nxt][0] = onnea , fa [onnea] = nxt ;
	zt( nxt ) , zt( root ) ;
}

void work(){
	dfs( 1 ) , ins( -Inf , 0 , 0 ) , ins( Inf , 0 , 0 ) ;
	m = read() ;
	while( m -- ){
		scanf( "%s" , bt ) ;
		if( bt [0] == 'Q' ) x = read() , Ask() ;
		if( bt [0] == 'F' ) x = read() , y = read() , Cge() ;
		if( bt [0] == 'C' ) x = read() , y = read() , Azt() ;
	}
}

signed main(){	
	sc() ;
	work() ;
	return 0 ;
}