容斥原理详解

这个东西给我学傻了，所以打算好好搞搞这个东西
先加个链接，写的很清楚：https://blog.csdn.net/m0_37286282/article/details/78869512

First.小问题加深理解

1.有一个0-9十个数字构成的排列，（0可以作首位），要求这个排列第一位数字大于\(1\)，最后一位小于\(8\)，问一共有多少种排列

解法一：暴力组合
其实这个东西不就是分情况吗

如果第一位数字大于等于8（也就是8-9）,则有\(C(2,1)*C(8,1)*A(8,8)=645120\)种选法
如果第一位数字小于8(也就是2-7),则有\(C(6,1)*C(7,1)*A(8,8)=1693440\)种选法

根据加法原理，我们把它加起来，就可以得到全集，也就是\(2338560\)种选法

解法二：容斥原理
先考虑所有排列情况，一共有\(A(10,10)=3628800\)种选法
在考虑原问题对全排列的补集，即

选出十个数字，使得第一个数小于等于1或者最后一个数大于等于8

如果可以求出来这个补问题的解，用全集减去就是答案
在考虑怎么得到这个问题的解，假设第一个数字小于等于1这个事件是\(X\)，最后一个数字大于等于8这个事件是\(Y\),那么原问题就是\(X*Y=|X|+|Y|-|X+Y|\)，也就是它的总数就是

容：第一个数字小于等于1,一共有\(C(2,1)*A(9,9)=725760\)
容：最后一个数字大于等于8,一共有\(C(2,1)*A(9,9)=725760\)
斥：第一个数字小于等于1并且最后一个数字大于等于8,一共有\(C(2,1)*C(2,1)*A(8,8)=161280\)

那么，补集的情况一共有\(725760+725760-161280=1290240\)种选法，再用\(A(10,10)-1290240=2338560\),最终答案一样

在这个问题中，我们通过两次容斥解决了要求相互影响需要分类讨论的情况，先通过第一次容斥把求交集转化为求并集，再通过第二次容斥转化求并集的问题，虽然看起来计算量大了，容斥并没有什么用处，但对于简化分类讨论，对于大数据还是很有用的

2.（0,1,2）序列问题
一个长度为n的序列，n给出，要求0,1,2每个数字至少出现一次，问排列一共有多少种

如果用纯组合算法，先排列再去重再特判，想想就麻烦
考虑容斥，整个序列一共有\(3^n\)种排列同样的，我们转向它的逆问题。也就是不出现1或不出现2或不出现3的序列
我们定义\(A_i(i=0.1.2)\)表示不出现数字\(i\)的序列数，那么由容斥原理，我们得到该逆问题的结果为
那么，我们的答案就是\(|A*B*C|\)

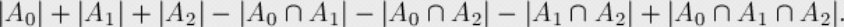
不出现一个数字，就是出现两个数字，那么他的排列方式就是\(2^n\)
不出现两个数字，就是出现一个数字，那么他的排列方式只有一种
三个数字都不出现，排列方式为0

答案就是\(3^n-3*2^n+3*1^n-0\)