树形dp

树形dp模板也很固定，打出树形dp的模板之后，我们可以从最底部开始向上进行，并且我们可以枚举出来每一对直系父子，一般是通过子节点将信息传到父节点，并进行一系列操作。

例题

1.树形背包类

解决有依赖的背包问题，背包dp也有说，这里直接给一道例题

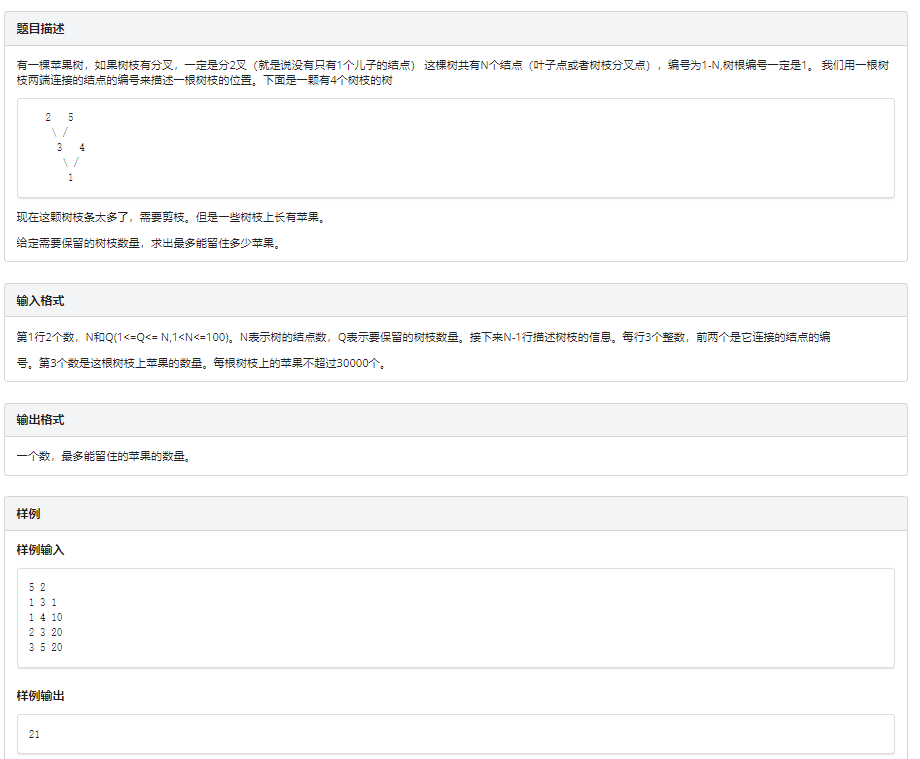
思路主要就是记得要给连接父子节点的边留出来一个位置，因为他必须选上，其余没什么了，\(\Large f [i][j]\)表示i子树留j条边的Max，答案就是\(\Large f[1][q]\)，i为根节点，q由题目给出

code

view code

#include<bits/stdc++.h>
#define int long long 
using namespace std ;

const int N = 110 ;
const int M = 1e4 + 10 ;

inline int read(){
    int w = 0 , f = 1 ; char ch = getchar() ;
    while( ch < '0' || ch > '9' ) { if( ch == '-' ) f = -1 ; ch = getchar() ; }
    while( ch >= '0' && ch <= '9' ){
        w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ;
        ch = getchar() ;
    } return f * w ;
}

int n , q ;
int f [N][N] ; // f -> i子树保留j条边的MAX 
struct E{ int to ; int next ; int w ;} a [M] ;
int head [N] , fg [N] , cnt ;
int size [N] ;

void addi( int x , int y , int w ){
    a [cnt].to = y ;
    a [cnt].w = w ;
    a [cnt].next = head [x] ;
    head [x] = cnt ++ ;
}

void sc(){
    memset( head , -1 , sizeof( head ) ) ; 
    int x , y , w ;
    n = read() , q = read() ;
    for( int i = 1 ; i < n ; i ++ )
    x = read() , y = read() , w = read() ,
    addi( x , y , w ) , addi( y , x , w ) ;
}

void dfs( int u , int fa ){
    for( int i = head [u] ; ~i ; i = a [i].next ){
        int y = a [i].to ;
        if( y == fa ) continue ;
        dfs( y , u ) ;
        size [u] += size [y] + 1 ; // when u == y , return 1 
        int be = min( size [u] , q ) ;
 //       printf( "%lld " , be ) ;
        for( int j = be ; j >= 1 ; j -- )
        for( int k = j - 1 ; k >= 0 ; k -- )
        f [u][j] = max( f [u][j] , f [u][j - k - 1] + f [y][k] + a [i].w ) ;
    }

}

void work(){
    dfs( 1 , 0 ) ;
    printf( "%lld" , f [1][q] ) ;
}

signed main(){
    sc() ;
    work() ;
    return 0 ;
}

2.信息传递类

这种问题父子节点之间一般都有一些羁绊，我们需要额外开一维来保存父子之间的状态，跟之前的带权并查集的思想有些类似

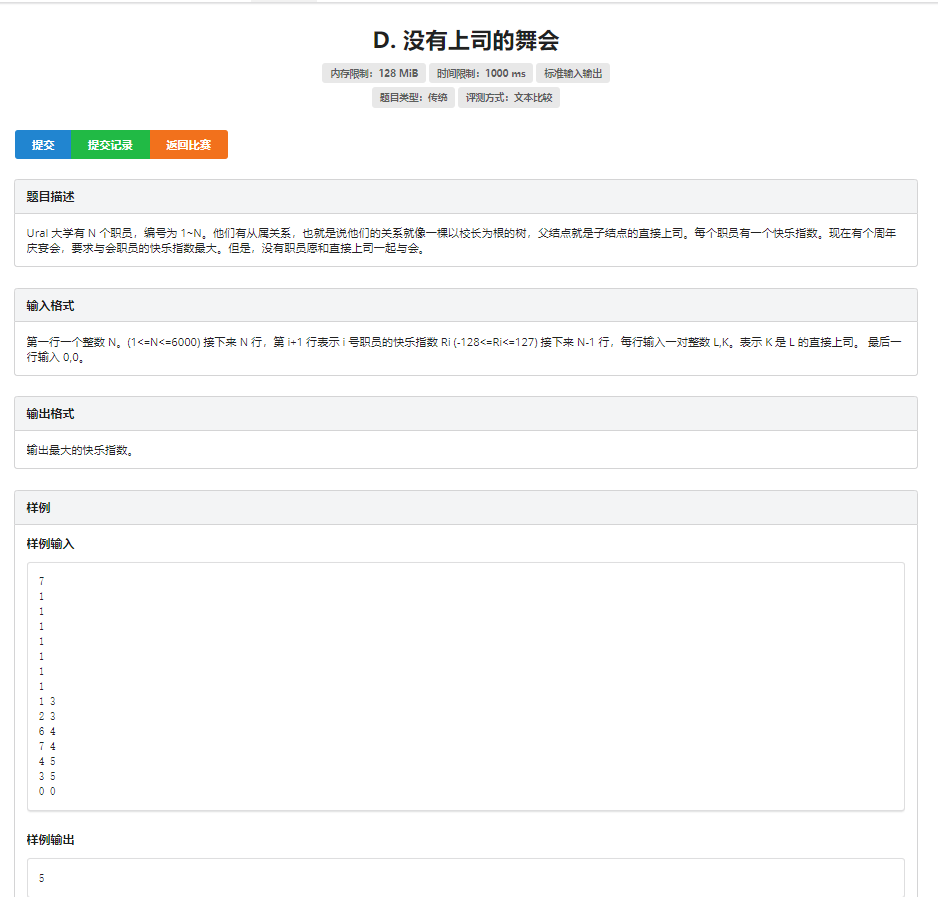
思路：这道题就是开两维，设u为上司，s为下属，则我们根据输入建造一棵树，用\(\Large f[k,i]\)来表示i节点的状态，\(k==0\)表示这个节点没有选，\(k==1\)表示选择了这个节点，直接给出关于每一对父子的方程，挺好理解的$$\Large f[0,u]=max(f[1,s],f[0,s])$$

\[\Large f[1,u]=f[0,s]+w[u] \]

当然，父节点要对子节点的信息进行求和，可以得到最终方程

\[\Large f[0,u]=\sum\limits_{s的父节点是u}max(f[1,s],f[0,s]) \]

\[\Large f[1,u]=(\sum\limits_{s的父节点是u}f[0,s])+w[u] \]

那么，找到根节点后\(\Large max(f[0,root],f[1,root])\)就是答案

code

view code

#include<bits/stdc++.h>
#define int long long 
using namespace std ;

inline int read(){
    int w = 0 , f = 1 ; char ch = getchar() ;
    while( ch < '0' || ch > '9' ) { if( ch == '-' ) f = -1 ; ch = getchar() ; }
    while( ch >= '0' && ch <= '9' ){
        w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ;
        ch = getchar() ;
    } return f * w ;
}

const int N = 2e4 + 10 ;

int n , f [2][N] ;
int w [N] ;
struct E{ int to , next  ; } t [N] ; 
int head [N] , cnt ;
bool fg [N] ;
int root ;

void addi( int to , int f ){
    t [cnt].to = to ;
    t [cnt].next = head [f] ;
    head [f] = cnt ++ ;
}

void sc(){
    int a , b ;
    n = read() ; memset( head , -1 , sizeof( head ) ) ;
    for( int i = 1 ; i <= n ; i ++ ) w [i] = read() ;
    for( int i = 1 ; i < n ; i ++ ) a = read() , b = read() , addi( a , b ) , addi( b , a ) , fg [a] = 1  ;
}

int fr(){
    for( int i = 1 ; i <= n ; i ++ ) 
    if( ! fg [i] ) {
        root = i ;
        return i ;
    }
}

void dfs( int root , int fa ){
    f [1][root] = w [root] ;
    for( int i = head [root] ; ~i ; i = t [i].next ){
        int y = t [i].to ;
        if( y == fa ) continue ;
        dfs( y , root ) ;
         f [0][root] += max( f [0][y] , f [1][y] ) ;
         f [1][root] += f [0][y] ;
    }
    
}

void work(){
    dfs( fr() , 0 ) ; 
    printf( "%lld" , max( f [0][root] , f [1][root] ) ) ;
}

signed main(){
    sc() ;
    work() ;
    return 0 ;
}

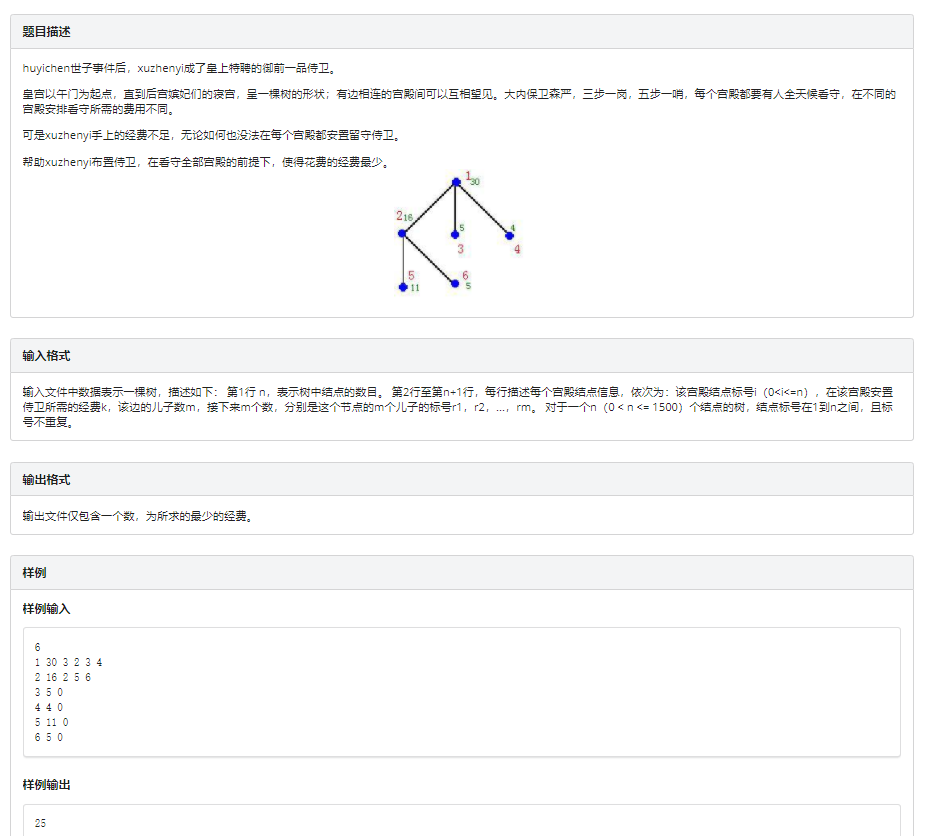
思路：这题其实是上一题的进化版，我们还是需要两维，一维存父子信息，另外一维表示节点。要想做出来这道题，首先要理解题意，我认为这题的题意是比较晦涩的，并且样例也很水，不利于我们理解题意，我当时看懂题花了半天，导致我一天才抠出来这道题，这个题的意思大概就是：给一棵树，我们可以选择守住某个节点，如果这个节点被守住了，那么与他相邻的所有节点都会被看住，守住每个节点都有对应的花费，问看住所有节点的最小花费

设状态\(\Large f[0,i],f[1,i],f[2,i]\)分别表示\(\Large i\)节点被自己，儿子，和父亲看住（被自己看住等于守住）

有了状态之后，我们考虑信息在父子节点之间的转移，如果一个节点被他自己看住了，那他的儿子可以选择让自己看，父亲看，或者儿子看中任意一种，因为反正它的儿子节点都已经被看住了

如果一个节点选择让他的儿子看，那么证明这个节点自己没有看人的能力，那他的儿子节点肯定不能选择让他的父亲看（如果这样他俩就起飞没人看了），他的众多儿子中可以选择自己看自己（也就是尽孝了，看住了父亲），也可以选择让儿子看自己（老败家子了）。但是，至少要有一个儿子看住父亲节点，因为父亲节点选择让儿子们看住他

如果这个节点选择让他的父亲看住，那么证明这个节点自己没有看人的能力，但这次对于儿子节点没有特殊要求，因为这个节点是让他的父亲看的。

我们便可以写出方程

\[\Large f[0,i]= (\sum \limits_{s是i的儿子} min(f[0,s],f[1,s],f[2,s]))+w[i] \]

\[\Large f[2,i]=(\sum\limits_{s是i的儿子}min(f[0,s],f[1,s])) \]

但是，怎么实现必须有一个儿子节点看住父亲节点呢？

我们思考，但凡有一个儿子的\(f[0,s]\)比\(f[1,s]\)小，这个父亲节点就被看住了，在没有比\(f[1,s]\)小的\(f[0,s]\)，我们需要加上一个最小的差价（\(f[0,s]-f[1,s]\)）,这样就可以使总花费最小

我们有两种方法可以实现上述思路

1. 用一个变量t来记录min（\(f[0,s]-f[1,s]\)）（只记录正数）,用一个bool变量来记录是否有\(f[0,s]\)比\(f[1,s]\)小，如果没有，再循环结束时为答案加上s
2. 每次都记录\(\Large t=\min\limits_{s是i的儿子}(f[0,s]-min(f[0,s],f[1,s]))\),在循环结束时为答案加上\(t\),这样，但凡有一个\(f[0,s]\)小于\(f[1,s]\)，那么\(t\)就会被记录成0，如果所有的\(f[0,s]\)都大于\(f[1,s]\)，那么t自然会记录最小的差值

有了上述思路，我们就可以写出方程

\[\Large f[2,i]=(\sum\limits_{s是i的儿子}min(f[0,s],f[1,s]))+\min\limits_{s是i的儿子}(f[0,s]-min(f[0,s],f[1,s])) \]

接下来打出板子写入方程即可

view code

#include <bits/stdc++.h>
using namespace std ;

const int N = 3e3 + 10 ;

inline int read(){
    int w = 0 ; char ch = getchar() ;
    while( ch > '9' || ch < '0' ) ch = getchar () ;
    while( ch >= '0' && ch <= '9' ){
        w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ;
        ch = getchar() ;
    } return w ;
}

bool fg [N] ;
int  root ;
int n , m , cnt ;
struct { int to ; int next ; } a [N] ;
int head [N] , w [N] ;
int f [8][N] ;  
 
void addi( int f , int t ){
    a [cnt].to = t ;
    a [cnt].next = head [f] ;
    head [f] = cnt ++ ;
//    printf( "ADDI%lld %lld\n" , f , head [f] ) ;
}

int thmax( int a , int b , int c ){
    a = max( a , b ) ;
    return max ( a , c ) ;
}

int thmin( int a , int b , int c ){
    a = min( a , b ) ;
    return min( a , c ) ;
}

void sc(){
    int shit , k , shits ;
    n = read() ; memset( head , -1 , sizeof( head ) ) ;
    for( int i = 1 ; i <= n ; i ++ ){
        shit = read() , w [shit] = read() , k = read() ;
//        if( k == 0 ) addi( i , 0 ) ;
        for( int j = 1 ; j <= k ; j ++ ){
            shits = read() ;
            fg [shits] = 1 ;
            addi( shit , shits ) ;
        }
    }
    for( int i = 1 ; i <= n ; i ++ )
    if( !fg [i] ) { root = i ; break ; } 
 /*   for( int i = 1 ; i <= n ; i ++ ){
        for( int j = head [i] ; ~j ; j = a [j].next ){
            printf( "%lld %lld %lld %lld\n" , i , a [j].to , j , a [j].next ) ;
        }
 //       printf( "HEAD%lld %lld\n" , i , head [i] ) ;
    }*/
}

void dfs( int u ){
    int mins = 1e9 ;
    for( int i = head [u] ; ~i ; i = a [i].next ){
        int y = a [i].to ;
        dfs( y ) ;

//        if( u == 4 ) printf( "shit" ) ;
        f [0][u] += min( min( f [0][y] , f [1][y] ) , f [2][y] ) ; //自己看，儿子中选最小的
        f [1][u] += min( f [0][y] , f [1][y] ) ;//父亲让儿子看 ，则儿子不能让父亲看 ，其余任选 ,但至少一个儿子要守住父亲 
        f [2][u] += min( f [0][y] , f [1][y] ) ; // 儿子让父亲看 ， 则孙子不能让儿子看
        mins = min( mins , f [0][y] - min( f [0][y] , f [1][y] ) ) ;
   //    printf( "%lld %lld %lld %lld %lld\n" , u , y , f [0][u] , f [1][u] , f [2][u] ) ;
    }
    f [0][u] += w [u] ; 
    f [1][u] += mins ;
}


void work(){
    dfs( root ) ;
    printf( "%lld" , min ( f [0][root] , f [1][root] ) ) ;
}


signed main(){
    sc() ;
    work() ;
    return 0 ;
}

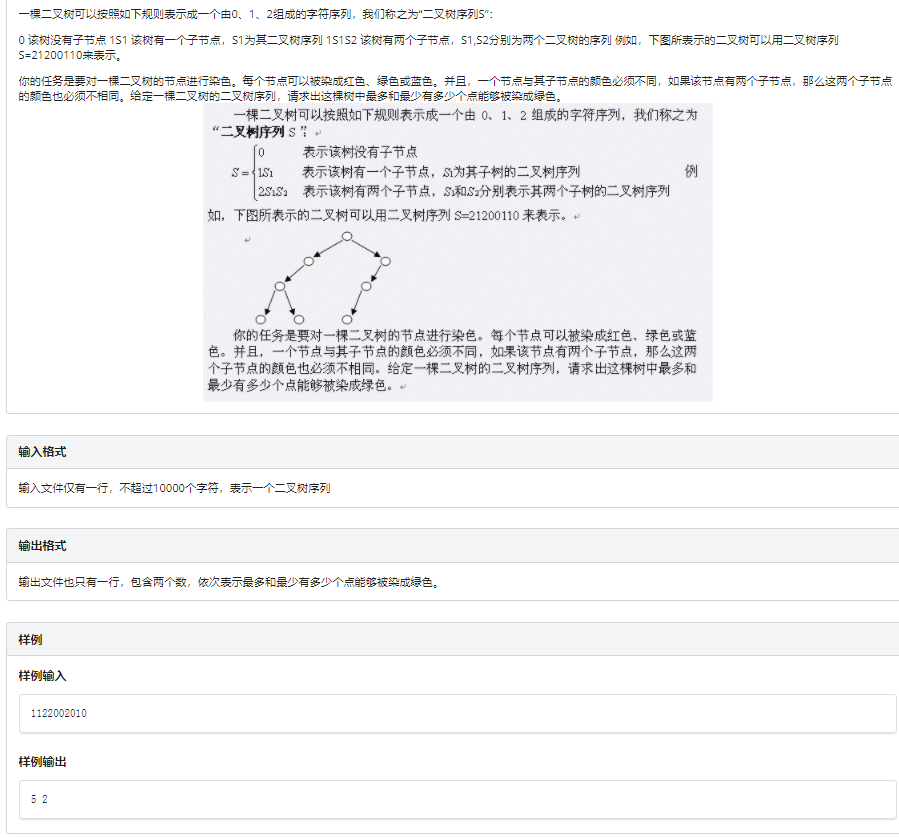
思路：其实这道题的方程还是很好推的，我们仍假设\(f[0,i],f[1,i],f[2,i]\)为图上绿色和红色，蓝色
由于颜色不能相邻，我们只需要让三个节点循环出现即可(\(\Large fin ,fax\)分别为最小值，最大值)

\[\Large fax [t][0] = max( fax [l][1] + fax [r][2], fax [l][2] + fax [r][1] ) + 1 \]

\[\Large fax [t][1] = max( fax [l][0] + fax [r][2], fax [l][2] + fax [r][0] ) \]

\[\Large fax [t][2] = max( fax [l][0] + fax [r][1], fax [l][1] + fax [r][0] ) \]

\[\Large fin [t][0] = min( fin [l][1] + fin [r][2], fin [l][2] + fin [r][1] ) + 1 \]

\[\Large fin [t][1] = min( fin [l][0] + fin [r][2], fin [l][2] + fin [r][0] ) \]

\[\Large fin [t][2] = min( fin [l][0] + fin [r][1], fin [l][1] + fin [r][0] ) \]

这道题建出来这个数来是有点难度的，通过递归建数是很常规很通用的思想，因为数就是通过递归定义的，也没什么好写的，具体见代码吧
code

view code

#include <bits/stdc++.h>
#define int long long
using namespace std ;

const int N = 1e7 + 10 ;
string s ; int head [N] ; int cnt ; 
int tr [N][2] ; 
int num ; int fax [N][3] , fin [N][3] ; // i , 0  green   i , 1 / 2 ~green 


void sc(){
	cin >> s ;
	memset( head , -1 , sizeof( head ) ) ;
}

int build(){
	int k = ++ num ;
	if( s [k - 1] == '2' )
	tr [k][0] = build() , tr [k][1] = build() ;
	else if( s [k - 1] == '1' )  tr [k][0] = build() ;
	return k ; 
}

int thmax( int a , int b , int c ){
	a = max( a , b ) ;
	return max( a , c ) ;
}

int thmin( int a , int b , int c ){
	a = min( a , b ) ;
	return min( a , c ) ;
}

void dfs( int t ){
//	printf( "%lld" , t ) ;
	int l = tr [t][0] , r = tr[t][1] ;
	if( l )  dfs( l ) ; if ( r )  dfs( r ) ;
	fax [t][0] = max( fax [l][1] + fax [r][2], fax [l][2] + fax [r][1] ) + 1 ;
	fax [t][1] = max( fax [l][0] + fax [r][2], fax [l][2] + fax [r][0] ) ;
	fax [t][2] = max( fax [l][0] + fax [r][1], fax [l][1] + fax [r][0] ) ;
	fin [t][0] = min( fin [l][1] + fin [r][2], fin [l][2] + fin [r][1] ) + 1 ;
	fin [t][1] = min( fin [l][0] + fin [r][2], fin [l][2] + fin [r][0] ) ;
	fin [t][2] = min( fin [l][0] + fin [r][1], fin [l][1] + fin [r][0] ) ;
}

void work(){
/*	for( int i = 0 ; i < num ; i ++ ){
		if( ! tr [i][0] && ! tr [i][1] )
		fax [i][0] = fin [i][0] = 1 ;
		fax [i][1] = fax [i][2] = 0 ;
		fin [i][1] = fin [i][2] = 0 ;
	}*/
//	printf( "%lld %lld %lld\n" , tr [i][0] , tr [i][1] , i ) ;
	dfs( 1 ) ;
	printf( "%lld %lld" , thmax( fax [1][1] , fax [1][0] , fax [1][2] ) , thmin( fin [1][2] , fin [1][1] , fin [1][0] ) ) ;
}


signed main(){
	sc() ;
	build() ;
	work() ;
	return 0 ;
}