坐标dp
坐标dp看起来和区间dp差别不大,其实差别还真不大还是有点差别的,区间dp \(\Large f[l,r]\)通常表示对于 \(\Large [l,r]\)这个区间最大值/最小是/总计数之类的,但是坐标dp \(\Large f(x,y)\)往往表示的是对于 \(\Large (x,y)\)这个点的一些操作(不一定非要是 \(\Large (x,y)\)的形式,具体见后面例题)
直接上题
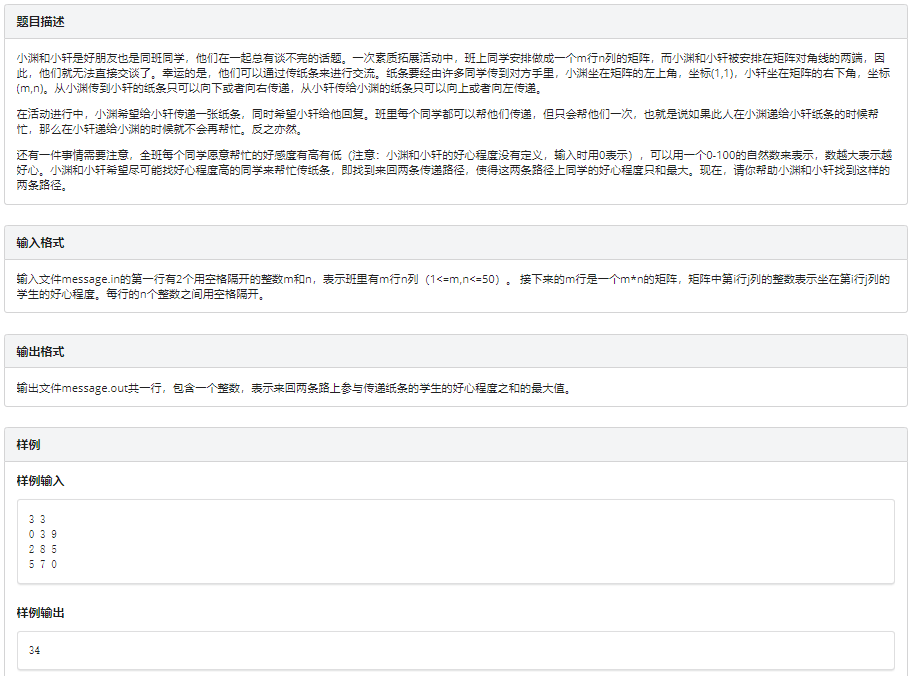
思路:其实感觉前面那个矩阵取数不就是加了for循环的区间dp吗?扩展一维你以为就能进化成坐标dp吗,这个题坐标dp的特性很明显,并且有些难度。
这道题目要求我们走两次,我们先考虑走一次的情况,我们假设\(\Large f[i][j]\)是他走到\(\Large (i,j)\)为止得到的最大值,由于他只能向下或者向右走,故前一个状态只能由两个状态转移而来,我们不难写出方程
其中s[i][j]就是走到那的好心程度,由输入得到
很显然,对于走两次,我们并不能分开走两次,而是应该把走第二次看成一个约束,还记的之前的二维背包问题吗?其实这运用了同样的思想(包括二维最短路也是同样的思想),当限制条件多了一种,我们并没有方法通过次数的叠加来实现我们的目的的时候,我们就可以考虑给我们的状态加一个维度,来同时实现这两种约束。
对于本题,我们可以直接暴力加上一个坐标的维度,即两个维度写出方程
这这样就可以得到答案,时间复杂度为\(\Large \Theta(N^4)\),对于50来说是可以接受的,但是由于本题方向的唯二性(只能向左或者向下)和不停性(不能停下来不走),我们不难发现\(\Large i_1+j_1\ === i_2+j_2\)(三个等于代表恒等于),所以,我们可以令\(\Large k = i_1+j_1\),那么\(\Large k = i_2+j_2\),不难发现,其中k恰好就是走过的步数,那么我们可以用\(\Large f(k,i_1,i_2)\)来表示一个状态,其中\(\Large j_1=k-i_1,j_2=k-i_2\),这样,我们写出优化后的方程
时间复杂度是\(\Large \Theta(N^3)\)
这里还需要考虑几个小问题
如果\(\Large x_1==x_2\),我们只能加一次
考虑枚举的起始问题,由题,我们知道\(\Large 1\leqslant i\leqslant n,1\leqslant j\leqslant m\)由因为\(\Large j == k-i\),我们将其替换,得到i的范围\(\Large k-m\leqslant i\leqslant k-1\),综上所述\(\Large max(k-m,1)\leqslant i\leqslant min(n,k-1)\)
code
view code
#include<bits/stdc++.h>
using namespace std ;
const int N = 55 ;
inline int read(){
int w = 0 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) ch = getchar() ;
while( ch >= '0' && ch <= '9' ) {
w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ;
ch = getchar() ;
} return w ;
}
int n , m ;
int w [N][N] ;
int f [2 * N][N][N] ;
void sc(){
n = read() , m = read() ;
for( int i = 1 ; i <= n ; i ++ )
for( int j = 1 ; j <= m ; j ++ )
w [i][j] = read() ;
}
void work(){
for( int k = 2 ; k <= n + m ; k ++ ){
for( int x1 = max( k - m , 1 ) ; x1 <= min( n , k - 1 ) ; x1 ++ ){
for( int x2 = max( k - m , 1 ) ; x2 <= min( n , k - 1 ) ; x2 ++ ){
int t = w [x1][k - x1] ;
if( x1 != x2 || k - x1 != k - x2 ) t += w [x2][k - x2] ;
f [k][x1][x2] = max( f [k][x1][x2] , f [k - 1][x1 - 1][x2] + t ) ;
f [k][x1][x2] = max( f [k][x1][x2] , f [k - 1][x1 - 1][x2 - 1] + t ) ;
f [k][x1][x2] = max( f [k][x1][x2] , f [k - 1][x1][x2- 1] + t ) ;
f [k][x1][x2] = max( f [k][x1][x2] , f [k - 1][x1][x2] + t ) ;
}
}
}
printf( "%d" , f [m + n][n][n] ) ;
}
signed main(){
sc() ;
work() ;
return 0 ;
}
2
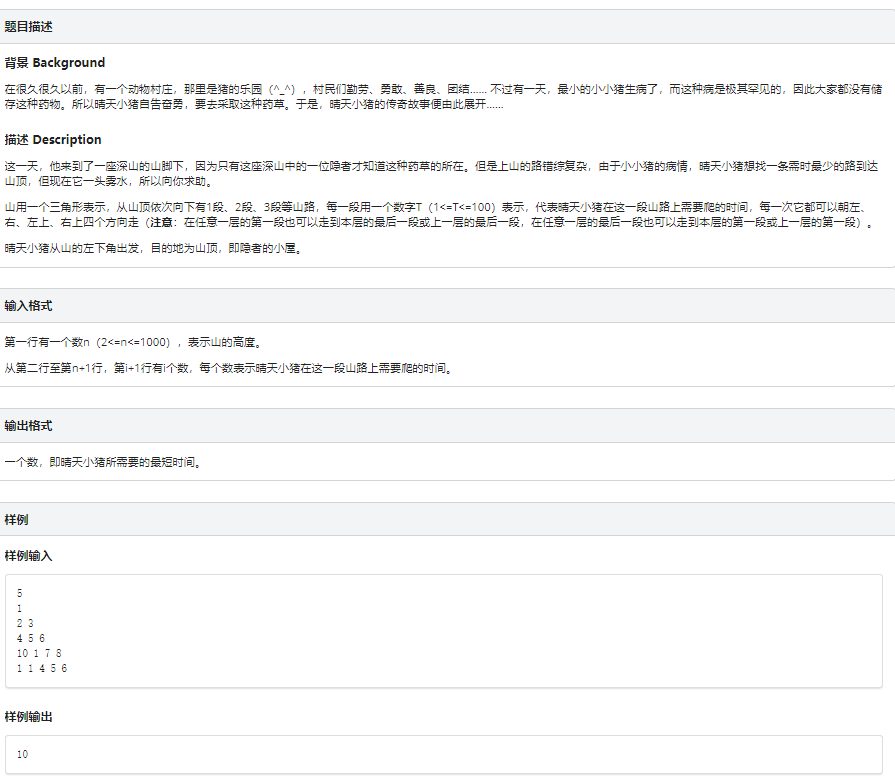
思路:这道题其实是一道加强版的数字金字塔,与金字塔不同的是它可以左右走,还是一个环形的结构,这个环形结构与区间dp中我们常见的破环为链的处理方法不同,如果题目中的山每一层宽度都一样,我们可以考虑破环为链,对于这道题来说,山的宽度从低到高逐渐减小,所以我们无法整体破环为链。但是,对于每一层来说,我们可以破环为链,然后进行刷新 。
总思路:先进行上下刷新,上下刷完之后,对于每一层,破环为链,左刷右刷就可以了
code
view code
#include<bits/stdc++.h>
#define R register int
#define int long long
using namespace std ;
const int N = 2e3 + 10 ;
inline int read(){
int w = 0 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) ch = getchar() ;
while( ch >= '0' && ch <= '9' ){
w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ;
ch = getchar() ;
} return w ;
}
int n ;
int w [N][2 * N] ;
int f [N][N] ;
int s [2 * N] ;
void sc(){
n = read() ;
memset( w , 127 / 3 , sizeof( w ) ) ;
for( int i = 1 ; i <= n ; i ++ )
for( int j = 1 ; j <= i ; j ++ )
w [i][j] = read() , w [i][i + j] = w [i][j] ;
f [1][1] = w [1][1] ;
}
void work(){
for( int i = 2 ; i <= n ; i ++ ){
for( int j = 1 ; j < i ; j ++ )
f [i][j] = min( f [i - 1][j] , f [i - 1][j - 1] ) + w [i][j] ;
int t = min( f [i - 1][1] , f [i - 1][i - 1] ) ;
f [i][1] = t + w [i][1] ;
f [i][i] = t + w [i][i] ;
//up down
/* for( int j = i - 1 ; j >= 1 ; j -- )
f [i][j] = min( f [i][j] , f [i][j + 1] + w [i][j] ) ;
f [i][i] = min( f [i][i] , f [i][1] + w [i][i] ) ;
for( int j = 2 ; j <= i ; j ++ )
f [i][j] = min( f [i][j] , f [i][j - 1] + w [i][j] ) ;
f [i][1] = min( f [i][1] , f [i][i] + w [i][1] ) ;*/
memset( s , 0 , sizeof( s ) ) ;
for( R j = 1 ; j <= i ; j ++ )
s [j] = f [i][j] , s [j + i] = f [i][j] ;
// for( R j = 1 ; j <= 2 * i ; j ++ )
// printf( "%lld " , s [j] ) ;
// s [1] = min( s [1] , s [n] + w [i][1] ) ;
for( R j = 2 ; j < 2 * i ; j ++ )
s [j] = min( s [j] , s [j - 1] + w [i][j] ) ;
for( R j = 2 * i - 1 ; j > 1 ; j -- )
s [j] = min( s [j] , s [j + 1] + w [i][j] ) ;
for( R j = 1 ; j <= i ; j ++ )
f [i][j] = min( s [j] , s [j + i] ) ;
// printf( "\n" ) ;
}
printf( "%lld" , f [n][1] ) ;
}
signed main(){
sc() ;
work() ;
return 0 ;
}
3
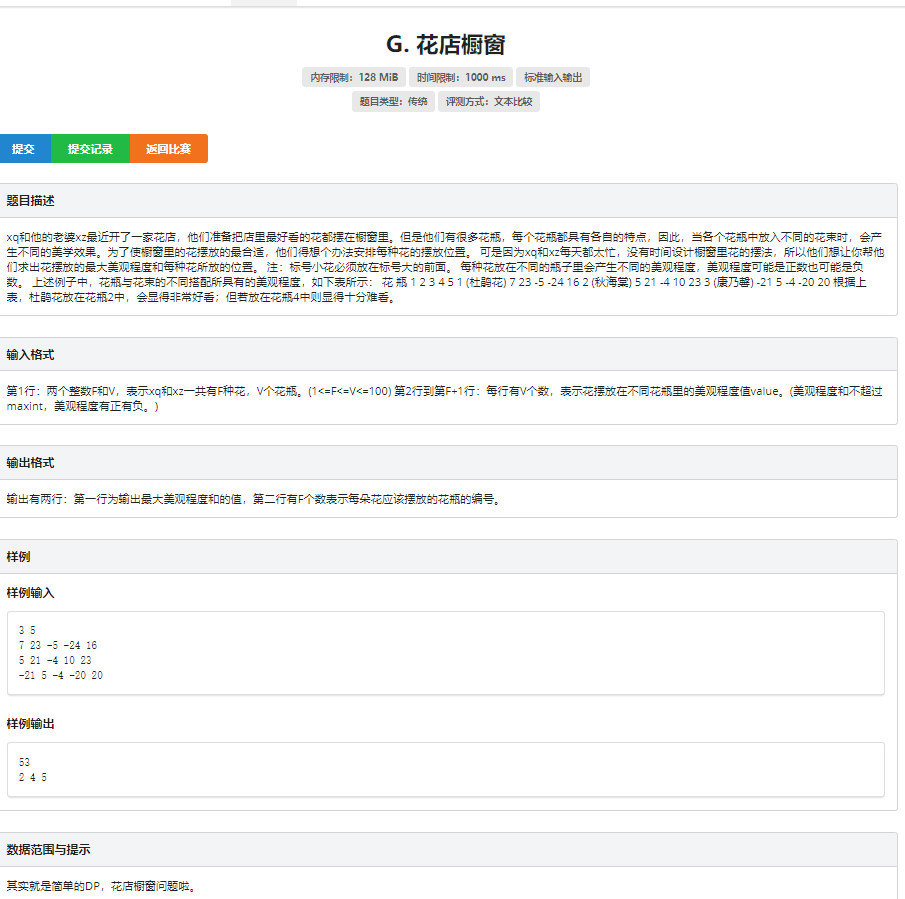
思路:其实这是一个各个区间中稍有羁绊的坐标dp,说他是区间dp也不是不可以,提取出来数学模型 。推区间dp的方程即可
摘自网上
给定一个f*v的矩阵
要求从第一行走到第f行,每行取走一个数,
且该行所取的数必须必上一行所取的数的列数大 , 求所能取走的最大值
注意每一行所取走的数字的列数必须大于等该行的行号
因为必须给前面的花留下足够的花瓶
同理每一行所能取的最大的花瓶号必须小于等于v-(f-该行行数)
由此我们便可以很容易的得出状态转移方程
其中\(dp[i][j]\)表示从第一行走到第i行并取走该行第j个数所能取得的最大值.
方案输出具体操作见路径记录专题
code
view code
#include<bits/stdc++.h>
using namespace std ;
const int N = 110 ;
inline int read(){
int w = 0 , f = 1 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ){
if( ch == '-' ) f = -1 ;
ch = getchar() ;
}
while( ch >= '0' && ch <= '9' ){
w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ;
ch = getchar() ;
}
return f * w ;
}
int F , v ;
int w [N][N] ;
int f [N][N] ; // 前i朵花放在前j个瓶子内最大利益
int path [N][N] ;
void sc(){
F = read() , v = read() ;
for( int i = 1 ; i <= F ; i ++ )
for( int j = 1 ; j <= v ; j ++ )
w [i][j] = read() ;
memset( f , - 127 / 3 , sizeof( f ) ) ; // 由于可能为观赏度可能为负的
}
void work(){
for( int i = 1 ; i <= F ; i ++ ) f [0][i] = 0 ;
for( int i = 1 ; i <= v ; i ++ ) f [1][i] = w [1][i] ;
for( int i = 2 ; i <= F ; i ++ ){
for( int j = i ; j <= v - ( F - i ) ; j ++ ){//留给后面的瓶子
for( int k = i - 1 ; k < j ; k ++ ){//枚举决策点
if( f [i - 1][k] + w [i][j] > f [i][j] ){
f [i][j] = f [i - 1][k] + w [i][j] ;
path [i][j] = k ;
// printf( "%lld %lld %lld\n" , i , j , path [i] ) ;
}
}
}
}
int anss = 0 , ansi = 0 ;
for( int i = 1 ; i <= v ; i ++ )
if( f [F][i] > anss ) anss = f [F][i] , ansi = i ;
printf( "%d\n" , anss ) ;
int ans[N] ; ans [F] = ansi ;
for( int i = F ; i >= 2 ; i -- )
ans [i - 1] = path[i][ans [i]] ;
for( int i = 1 ; i <= F ; i ++ )
printf( "%d " , ans [i] ) ;
}
signed main(){
sc() ;
work() ;
return 0 ;
}
4
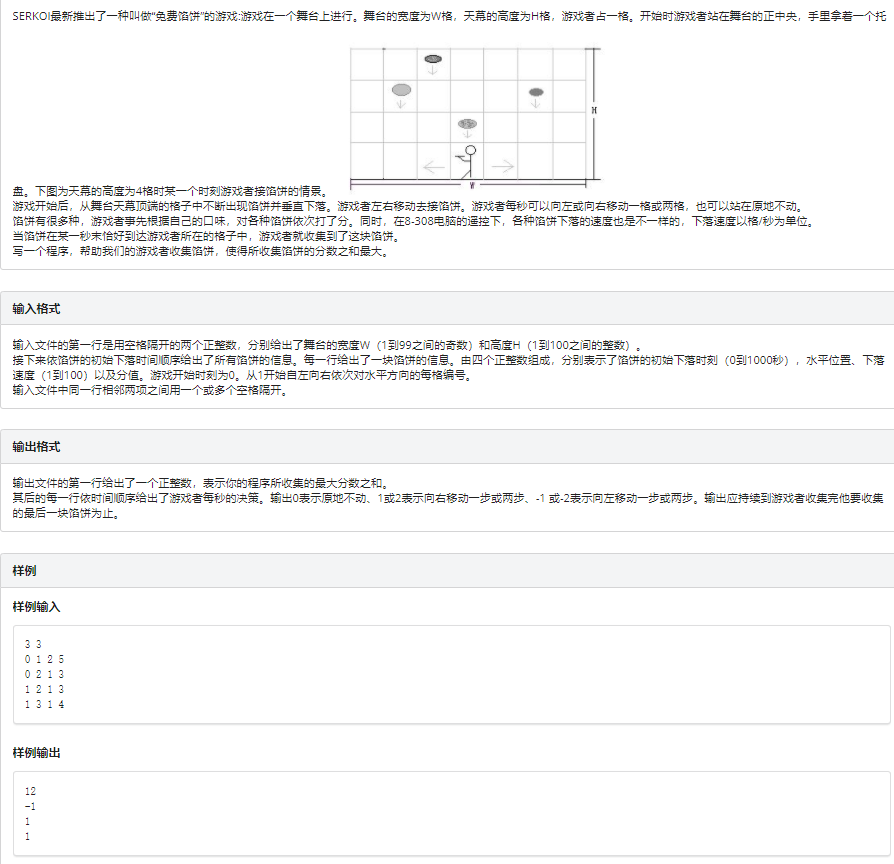
思路:根据题目分析,我们设\(\Large f[i,j]\)为i时刻在j位置所得到的最大分数,那么\(\Large max(f[las,k])\|k\in[1,w]\)就是答案,其中w为场地的宽度,las为最后的时间
不难发现,一个状态可以由五个状态转移而来,分别是:不动,左1,左2,右1,右2;
写出方程:
\(w[i,j]\)为i时刻在j位置的得分
路径记录见路径记录专题
code
view code
#include<bits/stdc++.h>
#define int long long
using namespace std ;
inline int read(){
int w = 0 ; char ch = getchar() ;
while( ch > '9' || ch < '0' ) ch = getchar() ;
while( ch >= '0' && ch <= '9' ){
w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ;
ch = getchar() ;
} return w ;
}
const int N = 1e2 + 10 ;
const int M = 1e3 + 10 ;
int s , h ;
int w [M][N] ;
int f [M][N] ;
int path [M][N] ;
int las , ct ;
void sc(){
s = read() , h = read() , h -- ;
ct = s / 2 ; ct ++ ;
int t , x , v , ws , rt ;
while( ~scanf( "%lld" , &t ) ){
x = read() , v = read() , ws = read() ;
if( h % v == 0 )
rt = t + ( h / v ) ;
las = max( las , rt ) ;
w [rt][x] += ws ;
} //printf( "%lld %lld" , ct , las ) ;
/* for( int i = 1 ; i <= s ; i ++ )
for( int j = 1 ; j <= 10 ; j ++)
printf( "%lld %lld %lld\n" , i , j , w [i][j] ) ; */
}
void work(){
memset( f , -1 , sizeof( f ) ) ;
f [0][ct] = 0 ;
for( int i = 1 ; i <= las ; i ++ ){
for( int j = 1 ; j <= s ; j ++ ){
int t = w [i][j] ;
for( int k = -2 ; k <= 2 ; k ++ ){
if( j + k < 1 || j + k > s ) continue ;
if( f [i][j] < f [i - 1][j + k] + t ){
f [i][j] = f [i - 1][j + k] + t ;
path [i][j] = -k ;
}
}
}
}
int ans = 0 , maxx = 0 , maxy = 0 ;
for( int i = 1 ; i <= las ; i ++ ){
for( int j = 1 ; j <= s ; j ++ ){
if( f [i][j] > ans ){
ans = f [i][j] ;
maxx = i , maxy = j ;
}
}
}
printf( "%lld\n" , ans ) ;
stack<int> a;
while( maxx ){
// printf( "%lld %lld %lld\n" , maxx , maxy , path [maxx][maxy] ) ;
a.push( path [maxx][maxy] ) ;
maxy -= path [maxx][maxy] ;
maxx -- ;
}
while( !a.empty() ){
printf( "%lld\n" , a.top() ) ;
a.pop() ;
}
}
signed main(){
sc() ;
work() ;
return 0 ;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号