区间dp
其实区间dp是板子最固定的,本文写出板子并附带几道例题
正文
1. 板子
for( 枚举区间的长度 ){
for( 枚举左端点 ){
得到右端点
for( 枚举操作【从左端点到右端点】 )
}
}
//example:
for( int len = 2 ; len <= n ; len ++ ){
for( int l = 1 ; l + len <= 2 * n + 1 ; l ++ ){
int r = l + len - 1 ;
for( int k = l ; k < r ; k ++ ){
if( signs [k + 1] == 1 )
f [l][r] = max ( f [l][r] , f [l][k] + f [k + 1][r] ) ,
s [l][r] = min ( s [l][r] , s [l][k] + s [k + 1][r] ) ;
else{
int a = max ( s [l][k] * s [k + 1][r] , f [l][k] * f [k + 1][r] ) ;
int b = max ( f [l][k] * s [k + 1][r] , s [l][k] * f [k + 1][r] ) ;
int as = max( a , b ) ;
int c = min ( s [l][k] * s [k + 1][r] , f [l][k] * f [k + 1][r] ) ;
int d = min ( f [l][k] * s [k + 1][r] , s [l][k] * f [k + 1][r] ) ;
int bs = min( c , d ) ;
f [l][r] = max( f [l][r] , as ) ;
s [l][r] = min( s [l][r] , bs ) ;
}
}
}
}
常见:
for( R len = 2 ; len <= n ; len ++ ){
for( R l = 1 ; l + len <= n + 1 ; l ++ ){
int r = l + len - 1 ;
for( R k = l ; k < r ; k ++ ){
各种操作
.......
}
}
}
粘贴课件
合并:意思就是将两个或多个部分进行整合,当然也可以反过来,也就是是将一个问题进行分解成两个或多个部分。
特征:能将问题分解成为两两合并的形式
求解:对整个问题设最优值,枚举合并点,将问题分解成为左右两个部分,最后将左右两个部分的最优值进行合并得到原问题的最优值。有点类似分治算法的解题思想。
2. 例题
1.经典区间dp
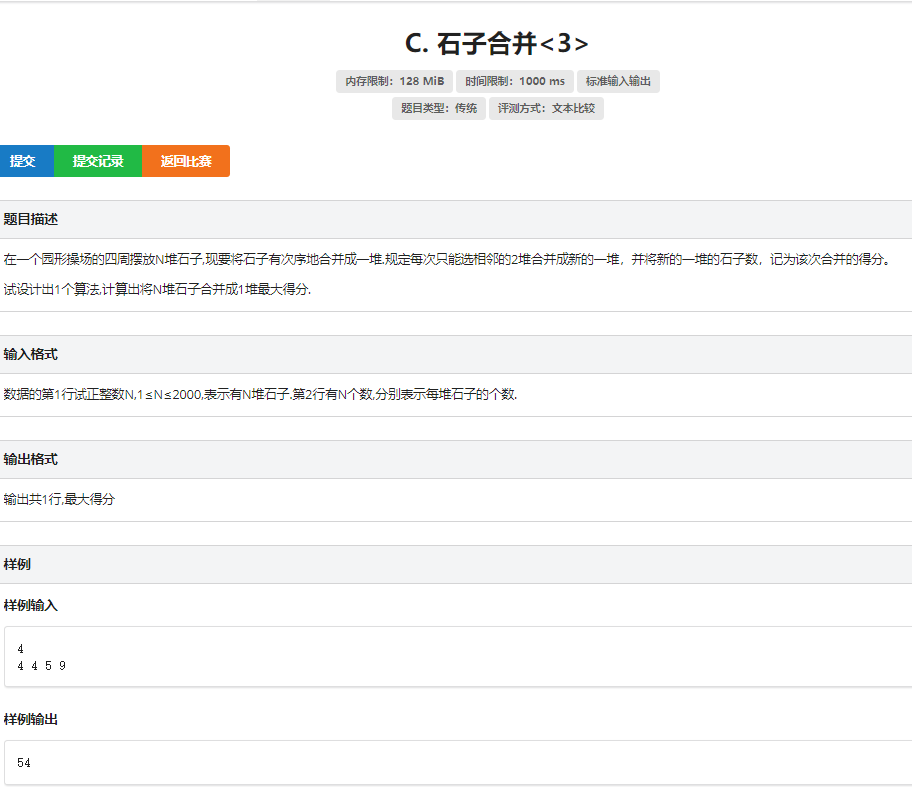
额外的问题:求最小值 ;
思路:对于这道题,首先要处理他是一个环的问题,我们有经典的破环为链,将这个链复制一遍粘贴到这条链的尾端,那么在环里面的所有操作在这条链里面也就都有了,搞成一个链之后,我们再考虑如何合并
对于一个区间 \(\Large[l,r]\) 我们用 \(\Large f[l,r]\) 来表示合并成\(\Large[l,r]\) 所得到的最大分数,那么很显然\(\Large max_{k=0}^{n-1}( f[1+k,n+k] )\) 就是答案,边界条件也很好找,当一堆石子没有进行合并的时候, \(\Large l == r\) , 则所有的 \(\Large f[][]\) 应该初始化为 \(0\) 。
我们还需要一个前缀和,这样我们就可以快速得到合并后的得分
接下来考虑状态转移
对于一个区间 \(\Large f[l,r]\) 他肯定由两个区间合并而成,所以,我们只需要它的合并点也就是断点,就可以写出方程,对于断点,枚举即可。\(\Large s[l,r]\)表示前缀和\(\Large t[r]-t[l-1]\),就也是合并所得到的分数。
方程(max):$$\Large f[l,r]=max(f[l,r],f[l,k]+f[k+1,r])+s[l,r]|k\in[l,r)$$
方程(min):$$\Large f[l,r]=min(f[l,r],f[l,k]+f[k+1,r])+s[l,r]|k\in[l,r)$$
但是这个时间复杂度是\(\large \Theta(N^3)\)的,很显然对于\(N \leqslant2000\)的数据范围来说我们是无法接受的
优化:求最大值
根据最大值的性质,它只能在两个端点取到

没事,知道你看到肯定\(\LARGE 非常懵逼\),这不重要,接下来手写一下证明(其实是看的课件然后自己证明了一遍)
证明
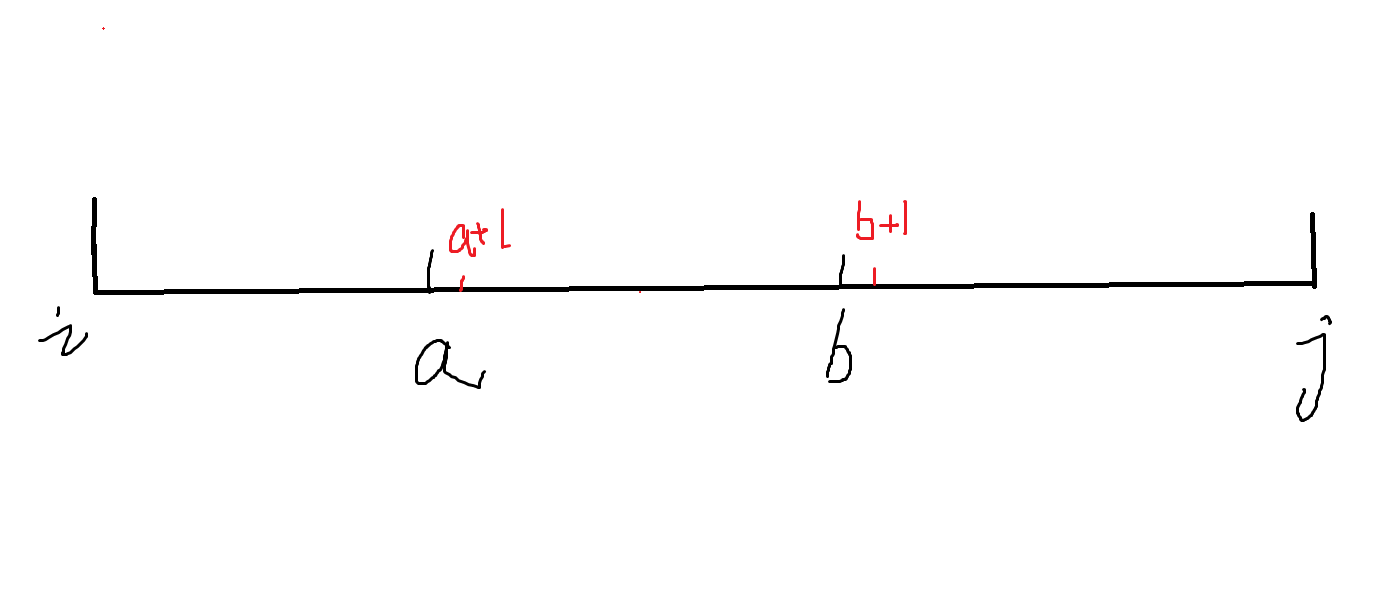
(蒟蒻亲手画图)
假设我们有两个决策点,分别对应两种决策方案
决策方案1表示我们在a点决策,决策方案2表示我们b点决策
如果我们在a点决策,那么我们需要将 \(\Large f[i,a]和f[a+1,j]\)合并,得到\(\Large f[i][j]\) 的表示。(\(s[i][j]\)为合并为\([i,j]\)这个区间所得到的分)
同理,我们写出在b点决策的方程
这个式子到这里我们是比不出大小的,所以我们考虑再次分割
我们将\(\Large [a+1,j]\)拆成\(\Large [a+1,b]\)和\(\Large [b+1,j]\)
写出拆完之后的方程
同理,将\(\Large [i,b]\)拆成\(\Large [i,a]\)和\(\Large [a+1,b]\)
将3柿带入1柿得到5柿,将4柿带入2柿得到6柿
我们可以得到
对于两种决策,我们做差 得到
所以我们只需要比较\(\Large s[a+1][j]和s[i][b]\)的大小即可
如果\(\Large s[i,b] \leqslant s[b+1,j]\)我们可以得到
\(\Large s[i,b] \leqslant s[b+1,j] < s[a+1,j]\)这种情况下,在a点决策更优,接着,我们发现,a点越靠左,\(\Large s[a+1,j]\)比\(\Large s[b+1,j]\)大的也就越多,所以我们要尽可能偏靠左边决策,最左边也就是\(\Large i+1\)
如果\(\Large s[i,b] > s[b+1,j]\)同理我们可以发现越靠右决策利益更大,最右边也就是\(\Large j-1\)
对于最小值,其实需要平行四边形优化,这个以后再说吧
code
view code
#include<bits/stdc++.h>
using namespace std ;
const int N = 4010 ;
inline int read(){
int w = 0 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) ch = getchar() ;
while( ch >= '0' && ch <= '9' ){
w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ;
ch = getchar() ;
} return w ;
}
int n , s [N][N] , f [N][N] ;
int num [N] ;
void sc(){
n = read() ;
for( int i = 1 ; i <= n ; i ++ )
num [i] = read() , num [i + n] = num [i] ;
for( int i = 1 ; i <= 2 * n - 1 ; i ++ ){
int p = num [i] ;
for( int j = i + 1 ; j <= 2 * n - 1 ; j ++ ){
p += num [j] ;
s [i][j] = p ;
}
}
// for( int i = 1 ; i < 2 * n ; i ++ )
// printf( "%lld " , s [i] ) ;
}
void maxwork(){
for( int l = 2 * n - 1 ; l >= 1 ; l -- ){
for( int r = l ; r < 2 * n ; r ++ ){
f [l][r] = max( f [l + 1][r] , f [l][r - 1] ) + s [l][r] ;
}
}
int ans = 0 ;
for( int i = 1 ; i <= n ; i ++ )
ans = max( ans , f [i][i + n - 1] ) ;
printf( "%d\n" , ans ) ;
}
signed main(){
sc() ;
maxwork() ;
return 0 ;
}
由于模板过于固定,复制粘贴的题就不写了,写几个稍有思维含量的题
2.
思路:其实,对于每一次删除一条边,都是将两个点和一条边进行合并(考虑成将两堆石子合并),到最后剩一个点,其实就是剩下的那一堆石子我们在此关注的只是最后一堆石子的大小。
想明白这个之后,我们开始实现思路,通过破环为链来实现第一次白拆开的那一条边,将\(\Large f[i][i]\)存储当前节点的大小,然后进行的就是普通的区间dp了,注意这题可能出现负数,所以我们考虑存最大值和最小值(我当时也是WA了很多遍才发现),乘积的时候比较最小值的积和最大值的积存到最大值里面,最后遍历\(1\backsim n\)求一下破环为链的最值就可以了(本文主要讲解方程转移,路径记录见路径记录专题)
code
view code
#include<bits/stdc++.h>
#define int long long
using namespace std ;
const int N = 600 ;
inline int read(){
int f = 1 , w = 0 ; char ch = getchar() ;
while( ch > '9' || ch < '0' ) {
if ( ch == '-') f = -1 ;
ch = getchar() ;
}
while( ch >= '0' && ch <= '9' ){
w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ;
ch = getchar() ;
} return f * w ;
}
int n ;
int signs [N] ; // -1 -> * , 1 -> +
int nums [N] ;
int cnt1 , cnt2 ;
int f [N][N] ;
int s [N][N] ;
bool fg [N] ;
bool fgs ;
void sc(){
n = read() ;
char ch ; int p ;
for( int i = 1 ; i <= 2 * n ; i ++ ){
if( i % 2 ){
scanf( "%c" , &ch ) ;
if( ch == 'x' )
signs [++ cnt2] = -1 ;
else
signs [++ cnt2] = 1 ;
if ( !fgs && cnt2 > 1 ){
if( signs [cnt2] != signs [cnt2 - 1] )
fgs = 1 ;
}
}
else{
p = read() ;
nums [++ cnt1] = p ;
}
}
for( int i = 1 ; i <= n ; i ++ )
nums [i + n] = nums [i] , signs [i + n] = signs [i] ;
// for( int i = 1 ; i <= 2*n ; i ++ )
// printf( "%lld %lld\n" , nums [i] , signs [i] ) ;
memset( f , -127 / 3 , sizeof( f ) ) ;
memset( s , 127 / 3 , sizeof( s ) ) ;
for( int i = 1 ; i <= 2 * n ; i ++ )
f [i][i] = nums [i] , s [i][i] = nums [i] ;
}
void work(){
for( int len = 2 ; len <= n ; len ++ ){
for( int l = 1 ; l + len <= 2 * n + 1 ; l ++ ){
int r = l + len - 1 ;
for( int k = l ; k < r ; k ++ ){
if( signs [k + 1] == 1 )
f [l][r] = max ( f [l][r] , f [l][k] + f [k + 1][r] ) ,
s [l][r] = min ( s [l][r] , s [l][k] + s [k + 1][r] ) ;
else{
int a = max ( s [l][k] * s [k + 1][r] , f [l][k] * f [k + 1][r] ) ;
int b = max ( f [l][k] * s [k + 1][r] , s [l][k] * f [k + 1][r] ) ;
int as = max( a , b ) ;
int c = min ( s [l][k] * s [k + 1][r] , f [l][k] * f [k + 1][r] ) ;
int d = min ( f [l][k] * s [k + 1][r] , s [l][k] * f [k + 1][r] ) ;
int bs = min( c , d ) ;
f [l][r] = max( f [l][r] , as ) ;
s [l][r] = min( s [l][r] , bs ) ;
}
}
}
}
int ans = 0 ;
for( int i = 1 ; i <= n ; i ++ )
ans = max( ans , f [i][i + n - 1] ) ;
printf( "%lld\n" , ans ) ;
for( int i = 1 ; i <= n ; i ++ ){
if( f [i][i + n - 1] == ans )
printf( "%lld " , i ) ;
}
/* if( ! fgs ){
for( int i = 1 ; i <= n ; i ++ )
printf( "%lld " , i ) ;
exit( 0 ) ;
}*/
/* else{
}*/
}
signed main(){
sc() ;
work() ;
return 0 ;
}
3.低价回文
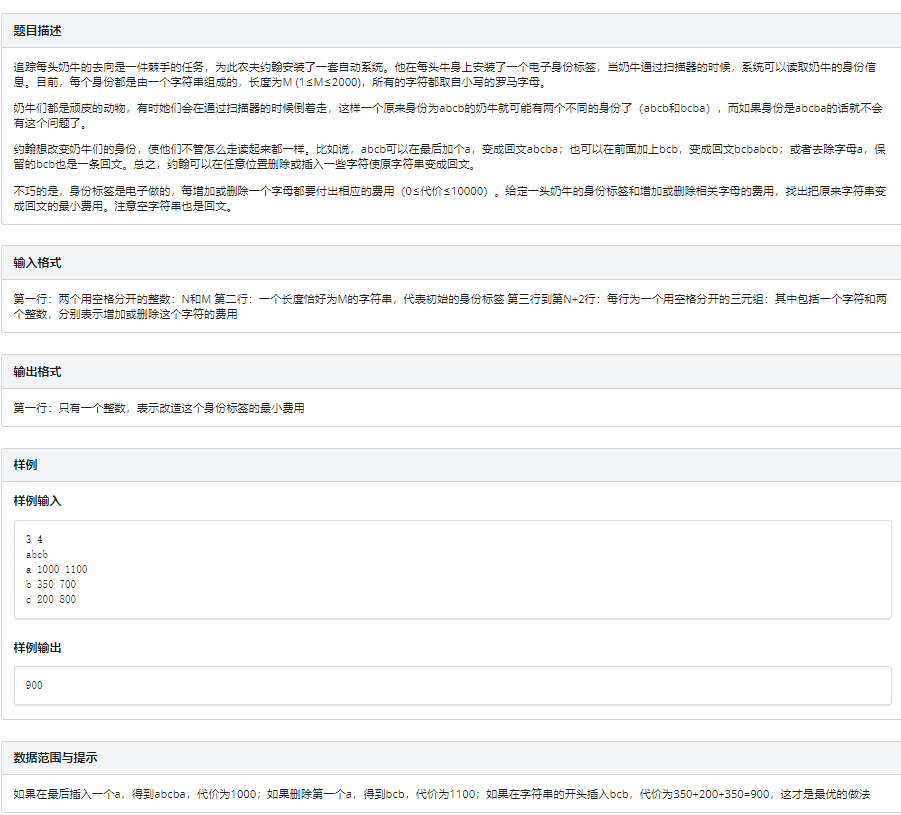
思路:其实这题主要需要想明白的就是其实加上一个字符和删去一个字符是等效的,都可以使得单个字母变成配好对的一对字母(空的也算配对),所以我们只需要在给出的两个信息中取最小值存下就可以了,我们设\(\Large f[i][j]\)为把\(\Large [i,j]\)这个区间变成回文的最小花费,那么\(\Large f[1][len]\)就是答案,其中len为字符串的长度
接下来推状态转移方程:
由于
区间dp模板打出来之后我们就可以得到题目区间的所有子区间的左右端点(这句话也就是区间dp的总结了)
所以,我们只需要在知道左右端点的情况下由其它状态推出一个状态即可,我们一个字母一个字母考虑
若对于一个区间:
1.其左端点字母等于右端点字母,那么
2.其左端点不等于右端点字母,那么,我们考虑用最小费用将他配对,也就是配对左端点和右端点中花费小的
这样状态转移就推完了
还有一个非常重要的问题,防倒吸!!
由于可能会出现在 f[i,j]中j小于i的情况,所以我们将所有的f[i,i-1]都手动赋值为0!!
code
view code
#include<bits/stdc++.h>
#define int long long
using namespace std ;
const int M = 4e3 + 10 ;
const int N = 1e3 + 10 ;
int n , lens ;
char a [M] ;
int c[N] ;
int f [M][M] ;
void sc(){
memset( f , 127 / 3 , sizeof( f ) ) ;
scanf( "%lld %lld" , &n , &lens ) ;
scanf( "%s" , a + 1 ) ;
char ch ; int as , bs ;
for( int i = 1 ; i <= n ; i ++ ){
cin >> ch >> as >> bs ;
c [ch] = min( as , bs ) ;
}
for( int i = 1 ; i <= lens ; i ++ )
f [i][i] = 0 , f [i][i - 1] = 0 ;
}
void work(){
for( int len = 2 ; len <= lens ; len ++ ){
for( int l = 1 ; l + len <= lens + 1 ; l ++ ){
int r = l + len - 1;
if( a [l] == a [r] )
f [l][r] = f [l + 1][r - 1] ;
else
f [l][r] = min( f [l + 1][r] + c [a [l]] , f [l][r - 1] + c [a [r]] ) ;
}
}
printf( "%lld" , f [1][lens] ) ;
}
signed main(){
sc() ;
work() ;
return 0 ;
}
由这题我们发现,第三层循环不一定要有,因为第三层循环是在枚举区间内的决策,区间dp的本质就是得到所有子区间并将它转化为其他区间,枚举断点只是一种决策方法,并不是必由之路,还需要根据具体的题目做灵活的处理。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号