背包Dp
终于来填坑啦!我才不会告诉你我是半天没有做出来一个题才来写的
其实背包九讲讲的已经非常清楚,我就是来复读一遍总结一下,其实看的时候还有一些自己的思考(比如自己推了一遍完全背包的柿子,写下来记录一下)
本文大部分内容来自背包九讲
正文
总写(背包九讲的目录)
第一讲 01背包问题
这是最基本的背包问题,每个物品最多只能放一次。
第二讲 完全背包问题
第二个基本的背包问题模型,每种物品可以放无限多次。
第三讲 多重背包问题
每种物品有一个固定的次数上限。
第四讲 混合三种背包问题
将前面三种简单的问题叠加成较复杂的问题。
第五讲 二维费用的背包问题
一个简单的常见扩展。
第六讲 分组的背包问题
一种题目类型,也是一个有用的模型。后两节的基础。
第七讲 有依赖的背包问题
另一种给物品的选取加上限制的方法。
第八讲 泛化物品
我自己关于背包问题的思考成果,有一点抽象。
第九讲 背包问题问法的变化
试图触类旁通、举一反三。
1 . 01背包
题目
有N件物品和一个容量为V的背包。第i件物品的费用是 \(c[i]\) ,价值是 \(w[i]\) 。求解将哪些物品装入背包可使价值总和最大。
基本思路
这是最基础的背包问题,特点是:每种物品仅有一件,可以选择放或不放。
用子问题定义状态:即 \(f[i][v]\) 表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。则其状态转移方程便是:
其实这是一个背包问题甚至所有dp方程的一个样板,状态转移方程其实就是描述状态是如何转移的,某一个状态肯定由其他状态转移而来。
对于01背包来说,他的任意一个状态都有两个状态转移而来,就是上一次放了物品或者放一次没放物品。
如果不放第i件物品,那么问题就转化为“前i-1件物品放入容量为v的背包中”,价值为 \(f [i-1][v]\)
如果放第i件物品,那么问题就转化为“前i-1件物品放入剩下的容量为 \(v-c[i]\) 的背包中”,此时能获得的最大价值就是 \(f[i-1][v-c[i]]\) 再加上通过放入第i件物品获得的价值 \(w[i]\) 。
空间优化
其实,如果方程中某一项跟且仅跟上一项有关,那么我们都可以进行空间优化去掉其中的一维,不过需要注意枚举的顺序
我们拿出原返程
\(\large f[i][v]=max\{ ( f[i-1][v],f[i-1][v-c[i]]+w[i] ) \}\)
发现,其中 \(i\) 仅与 \(i-1\) 有关,考虑空间优化,如果我们正序枚举,那么对于 \(f [v]\) 中存的其实就是 \(f [i-1][v]\) 的内容,当你枚举完这次之后, \(f [v]\) 中存的就是 \(f [i][v]\) 的值了,以此类推,我们可以通过i的正序枚举来实现空间优化
那么怎么枚举 \(V\) 呢?
这么考虑,由于一个物品只有一个,所以对于任意一个 \(i\) ,其 \(f [v]\) 的 \(max\) 只能是 \(f [i - 1][v] + w [i]\)
其实如果不优化空间,正序倒序枚举 \(V\) 其实无所谓,因为他就是从 \(i-1\) 转移过来的。
但是优化空间之后,若正序枚举 \(V\) ,那么可能会出现多次选择一个物品。例如,对于一个已经确定的 \(i\) , 我们从 \(cost[i]\) 进行枚举 ,那么 \(f [v-cost[i]]\) 代表已经选择了 \(i\) 这件物品,由于正序枚举加上空间优化的特性,当我们枚举比当前的 \(v\) 大的数的时候,导致 \(f [v]\) 中存的并不是 \(f[i-1][v]\) 而是已经刷新过的 \(f[i][v-cost[i]]\) 这样,就导致一个物品选多次的情况,从而产生了错误。所以我们只能倒叙枚举 \(V\) 。
其实这样的错误也并非没有用,由于它可以多次选择一个物品,我们就可以通过正序枚举来解决完全背包问题。
code
view code
#include<bits/stdc++.h>
#define M 110
#define N 1010
using namespace std ;
inline int read(){
int w = 0 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) ch = getchar() ;
while( ch >= '0' && ch <= '9' )
w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ,
ch = getchar() ;
return w ;
}
int v [M] , w [M] ;
int n , m ;
int f [N] ;
void sc(){
n = read() , m = read() ;
for( int i = 1 ; i <= m ; i ++ )
v [i] = read() , w [i] = read() ;
}
void work(){
for( int i = 1 ; i <= m ; i ++ )
for( int j = n ; j >= v [i] ; j -- )
f [j] = max( f [j] , f [j - v [i]] + w [i] ) ;
printf( "%lld" , f [n] ) ;
}
signed main(){
sc() ;
work() ;
return 0 ;
}
初始化问题
我们看到的求最优解的背包问题题目中,事实上有两种不太相同的问法。有的题目要求“恰好装满背包”时的最优解,有的题目则并没有要求必须把背包装满。一种区别这两种问法的实现方法是在初始化的时候有所不同。
如果是第一种问法,要求恰好装满背包,那么在初始化时除了f[0]为0其它f[1..V]均设为-∞,这样就可以保证最终得到的f[N]是一种恰好装满背包的最优解。
如果并没有要求必须把背包装满,而是只希望价格尽量大,初始化时应该将f[0..V]全部设为0。
为什么呢?可以这样理解:初始化的f数组事实上就是在没有任何物品可以放入背包时的合法状态。如果要求背包恰好装满,那么此时只有容量为0的背包可能被价值为0的nothing“恰好装满”,其它容量的背包均没有合法的解,属于未定义的状态,它们的值就都应该是-∞了。
如果背包并非必须被装满,那么任何容量的背包都有一个合法解“什么都不装”,这个解的价值为0,所以初始时状态的值也就全部为0了。
这个小技巧完全可以推广到其它类型的背包问题,后面也就不再对进行状态转移之前的初始化进行讲解。
2.完全背包
题目
有N种物品和一个容量为V的背包,每种物品都有无限件可用。第i种物品的费用是 \(c[i]\) ,价值是 \(w[i]\) 。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
基本思路
这个问题非常类似于01背包问题,所不同的是每种物品有无限件。也就是从每种物品的角度考虑,与它相关的策略已并非取或不取两种,而是有取0件、取1件、取2件……等很多种。
如果仍然按照解01背包时的思路,令 \(f[i][v]\) 表示前 \(i\) 种物品恰放入一个容量为v的背包的最大权值。仍然可以按照每种物品不同的策略写出状态转移方程,像这样:
这跟01背包问题一样有O(N*V)个状态需要求解,但求解每个状态的时间已经不是常数了,求解状态f[i][v]的时间是O(v/c[i]),总的复杂度是超过O(VN)的。
将01背包问题的基本思路加以改进,得到了这样一个清晰的方法。这说明01背包问题的方程的确是很重要,可以推及其它类型的背包问题。但我们还是试图改进这个复杂度。
一个简单有效的优化 (就是只要物美价廉的)
完全背包问题有一个很简单有效的优化,是这样的:若两件物品i、j满足c[i]<=c[j]且w[i]>=w[j],则将物品j去掉,不用考虑。这个优化的正确性显然:任何情况下都可将价值小费用高得j换成物美价廉的i,得到至少不会更差的方案。对于随机生成的数据,这个方法往往会大大减少物品的件数,从而加快速度。然而这个并不能改善最坏情况的复杂度,因为有可能特别设计的数据可以一件物品也去不掉。
这个优化可以简单的O(N^2)地实现,一般都可以承受。另外,针对背包问题而言,比较不错的一种方法是:首先将费用大于V的物品去掉,然后使用类似计数排序的做法,计算出费用相同的物品中价值最高的是哪个,可以O(V+N)地完成这个优化。
转化为01背包问题求解
既然01背包问题是最基本的背包问题,那么我们可以考虑把完全背包问题转化为01背包问题来解。
最简单的想法是,考虑到第i种物品最多选V/c[i]件,于是可以把第i种物品转化为V/c[i]件费用及价值均不变的物品,然后求解这个01背包问题。
这样完全没有改进基本思路的时间复杂度,但这毕竟给了我们将完全背包问题转化为01背包问题的思路:将一种物品拆成多件物品。
更高效的转化方法是:把第i种物品拆成费用为c[i]2k、价值为w[i]*2k的若干件物品,其中k满足c[i]2^k<=V。
这是二进制的思想,因为不管最优策略选几件第i种物品,总可以表示成若干个2^k件物品的和。这样把每种物品拆成O(log(V/c[i]))件物品,是一个很大的改进。
推转移方程(优化)
还是先给出原方程 \(\large f[i][v]=maxf[i-1][v-k * c[i]]+k * w[i]| 0<=k*c[i]<=v\)
将 \(f[i][j]中的k带入展开\) 得到:
\(\Large f[i][j] = max( f[i-1][j],f [i-1][j-v] + w , f [i-1][j-2*v] + 2*w , f [i-1][j-3*v] + 3*w , f [i-1][j-4*v] + 4*w ... )\)
我们在写出 \(f [i][j-v]\) 的柿子并将其中的 \(k\) 展开
\(\Large f[i][j-v]=max(f[i-1][j-v],f[i-1][j-2*v]+w,f[i-1][j-3*v]+2*w,f[i-1][j-4*v]+3*w,f[i-1][j-5*v]+4*w...)\)
不难发现,我们将第一个柿子从第二项开始看,第二个柿子从第一项开始看,会发现他们只差了一个w,所以错位相减之后,我们可以将第一个柿子第二项和第二项以后的项写成一个东西 \(f[i][j-v]+w\)
再将它带入第一个式子,得到
\(\large f[i][j] = max( f[i-1][j],f[i][j-v]+w)\) , 这样,我们就将k去掉了,优化了一层时间,但他有一个前提,观察柿子,我们不难发现,\(f[i][j]\) 这个状态除了需要我们在计算 \(f[i][j]\) 之前得到 \(f[i-1][j]\) 和 \(f[i][j-v]\) , 为了得到 \(f[i-1][j]\) ,我们考虑正序枚举 \(i\) , 为了得到 \(f[i][j-v]\) , 我们考虑正序枚举 \(v\) 。
这样,时间的优化就完成了
继续考虑优化掉空间
结合01背包不难想到,由于 \(i\) 的正序枚举,我们在用 \(f[j]\) 的时候它里面存的其实就是 \(f[i-1][j]\) , 我们再用 \(f[j-v]\) 的时候,由于 \(j\) 的正序枚举,它里面装的就是 \(f[i][j-v]\) , 所以我们直接去掉一维即可
所以我们得到方程
\(\large f[j]=max(f[j],f[j-v[i]]+w[i])\)
code
view code
#include<bits/stdc++.h>
#define N 30010
#define M 30
using namespace std ;
inline int read(){
int w = 0 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) ch = getchar() ;
while( ch >= '0' && ch <= '9' ){
w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ;
ch = getchar() ;
} return w ;
}
int v [M] , w [M] , f [N] ;
int n , m ;
void work(){
for( int i = 1 ; i <= m ; i ++ )
for( int j = v [i] ; j <= n ; j ++ )
f [j] = max( f [j] , f [j - v [i]] + w [i] ) ;
printf( "max=%lld" , f [n] ) ;
}
void sc(){
n = read() , m = read() ;
for( int i = 1 ; i <= m ; i ++ )
v [i] = read() , w [i] = read() ;
}
signed main(){
sc() ;
work() ;
return 0 ;
}
3.多重背包
题目
有N种物品和一个容量为V的背包。第i种物品最多有 \(n[i]\) 件可用,每件费用是 \(c[i]\) ,价值是 \(w[i]\) 。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
基本算法
\(这题目和完全背包问题很类似。基本的方程只需将完全背包问题的方程略微一改即可,因为对于第i种物品有 n[i]+1 种策略:取0件,取1件……取 n[i] 件。令f[i][v]表示前i种物品恰放入一个容量为v的背包的最大权值,则有状态转移方程:\)
复杂度是\(\large \Theta(\sum_{i=1}^N n[i] )\)
优化同样是二进制优化
转化为01背包问题
另一种好想好写的基本方法是转化为01背包求解:把第i种物品换成n[i]件01背包中的物品,则得到了物品数为Σn[i]的01背包问题,直接求解,复杂度仍然是O(V*Σn[i])。
但是我们期望将它转化为01背包问题之后能够像完全背包一样降低复杂度。仍然考虑二进制的思想,我们考虑把第i种物品换成若干件物品,使得原问题中第i种物品可取的每种策略——取0..n[i]件——均能等价于取若干件代换以后的物品。另外,取超过n[i]件的策略必不能出现。
方法是:将第i种物品分成若干件物品,其中每件物品有一个系数,这件物品的费用和价值均是原来的费用和价值乘以这个系数。使这些系数分别为1,2,4,...,2(k-1),n[i]-2k+1,且k是满足n[i]-2^k+1>0的最大整数。例如,如果n[i]为13,就将这种物品分成系数分别为1,2,4,6的四件物品。
分成的这几件物品的系数和为n[i],表明不可能取多于n[i]件的第i种物品。另外这种方法也能保证对于0..n[i]间的每一个整数,均可以用若干个系数的和表示,这个证明可以分0..2k-1和2k..n[i]两段来分别讨论得出。
这样就将第i种物品分成了O(log n[i])种物品,将原问题转化为了复杂度为O(V*Σlog n[i])的01背包问题,是很大的改进。
下面给出O(log amount)时间处理一件多重背包中物品的过程,其中amount表示物品的数量
code
view code
#include<bits/stdc++.h>
#define int long long
using namespace std ;
const int N = 100010 ;
const int M = 6010 ;
inline int read(){
int w = 0 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) ch = getchar() ;
while( ch >='0' && ch <= '9' ){
w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ;
ch = getchar() ;
} return w ;
}
int n , m ;
int v [N] , w [N] ;
int cnt = 0 ;
int f [M] ;
void sc(){
n = read() , m = read() ;
for( int i = 1 ; i <= n ; i ++ ){
int a , b , c ;
a = read() , b = read() , c = read() ;
for( int k = 1 ; k <= c ; k *= 2 ){
w [++ cnt] = a * k ;
v [cnt] = b * k ;
c -= k ;
}
if( c > 0 ) w [++ cnt] = a * c , v [cnt] = b * c ;
}
}
void work(){
for( int i = 1 ; i <= cnt ; i ++ )
for( int j = m ; j >= w [i] ; j -- )
f [j] = max( f [j] , f [j - w [i]] + v [i] ) ;
printf( "%lld" , f [m] ) ;
}
signed main(){
sc() ;
work() ;
return 0 ;
}
4.混合背包
问题
如果将P01、P02、P03混合起来。也就是说,有的物品只可以取一次(01背包),有的物品可以取无限次(完全背包),有的物品可以取的次数有一个上限(多重背包)。
思路
简单的混合即可,谁是什么类型就让他做什么背包
code
view code
#include<bits/stdc++.h>
#define int long long
using namespace std ;
const int N = 1e6 + 10 ;
const int M = 300 ;
inline int read(){
int w = 0 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) ch = getchar() ;
while( ch >= '0' && ch <= '9' ) {
w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ;
ch = getchar() ;
} return w ;
}
int m , n ;
struct E{
int v ;
int w ;
} a[N] ;
int s [M] ;
int f [M] ;
void sc(){
m = read() , n = read() ;
for( int i = 1 ; i <= n ; i ++ )
a [i].w = read() , a [i].v = read() , s [i] = read() ;
}
void O1( E i ){
for( int j = m ; j >= i.w ; j -- )
f [j] = max( f [j] , f [j - i.w] + i.v ) ;
}
void O2( E i ){
for( int j = i.w ; j <= m ; j ++ )
f [j] = max( f [j] , f [j - i.w] +i.v ) ;
}
void O3( int i ){
vector<E> e ;
for( int k = 1 ; k <= s [i] ; k *= 2 ){
s [i] -= k ;
e.push_back( { a [i].v * k , a [i].w * k } ) ;
}
if( s [i] ) e.push_back( { a [i].v * s [i] , a [i].w * s [i] } ) ;
for( int j = 0 ; j < e.size() ; j ++ ){
O1( e[j] ) ;
}
}
void work(){
for( int i = 1 ; i <= n ; i ++ ){
if( s [i] == 1 )
O1( a [i] ) ;
else if( !s [i] )
O2( a [i] ) ;
else
O3( i ) ;
}
printf( "%lld" , f [m] ) ;
}
signed main(){
sc() ;
work() ;
return 0 ;
}
5.二维背包
问题
二维费用的背包问题是指:对于每件物品,具有两种不同的费用;选择这件物品必须同时付出这两种代价;对于每种代价都有一个可付出的最大值(背包容量)。问怎样选择物品可以得到最大的价值。设这两种代价分别为代价1和代价2,第i件物品所需的两种代价分别为a[i]和b[i]。两种代价可付出的最大值(两种背包容量)分别为V和U。物品的价值为w[i]。
算法
费用加了一维,只需状态也加一维即可。设f[i][v][u]表示前i件物品付出两种代价分别为v和u时可获得的最大价值。状态转移方程就是:
如前述方法,可以只使用二维的数组:当每件物品只可以取一次时变量v和u采用逆序的循环,当物品有如完全背包问题时采用顺序的循环。当物品有如多重背包问题时拆分物品。
物品总个数的限制
有时,“二维费用”的条件是以这样一种隐含的方式给出的:最多只能取M件物品。这事实上相当于每件物品多了一种“件数”的费用,每个物品的件数费用均为1,可以付出的最大件数费用为M。换句话说,设f[v][m]表示付出费用v、最多选m件时可得到的最大价值,则根据物品的类型(01、完全、多重)用不同的方法循环更新,最后在f[0..V][0..M]范围内寻找答案。
扩展
对于这种问题,加一维,二维,三维都有可能,要灵活运用
code
view code
#include<bits/stdc++.h>
#define int long long
using namespace std ;
const int M = 410 ;
const int N = 100 ;
inline int read(){
int w = 0 ; char ch = getchar() ;
while( ch > '9' || ch < '0' ) ch = getchar() ;
while( ch >= '0' && ch <= '9' ) {
w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ;
ch = getchar();
} return w ;
}
int f [M][M] ;
int v , m , n ;
void sc(){
v = read() , m = read() , n = read() ;
for( int i = 1 ; i <= n ; i ++ ){
int va = read() , ma = read() , wa = read() ;
for( int j = v ; j >= va ; j -- )
for( int k = m ; k >= ma ; k -- )
f [j][k] = max( f [j][k] , f [j - va][k - ma] + wa ) ;
}
printf( "%lld" , f [v][m] ) ;
}
signed main(){
sc() ;
return 0 ;
}
6.分组背包
问题
有N件物品和一个容量为V的背包。第i件物品的费用是c[i],价值是w[i]。这些物品被划分为若干组,每组中的物品互相冲突,最多选一件。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
算法
这个问题变成了每组物品有若干种策略:是选择本组的某一件,还是一件都不选。也就是说设f[k][v]表示前k组物品花费费用v能取得的最大权值,则有:
同样的,我们发现k只与k-1有关,所以我们直接去掉一维。
注意这里的三层循环的顺序.
“for v=V..0”这一层循环必须在“for 所有的i属于组k”之外。这样才能保证每一组内的物品最多只有一个会被添加到背包中。
先枚举物品,再枚举体积,最后枚举决策
code
view code
#include<bits/stdc++.h>
#define int long long
using namespace std ;
const int M = 4100 ;
const int N = 1000 ;
const int T = 20 ;
inline int read(){
int w = 0 ; char ch = getchar() ;
while( ch > '9' || ch < '0' ) ch = getchar() ;
while( ch >= '0' && ch <= '9' ) {
w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ;
ch = getchar();
} return w ;
}
int f [M] ;
int t [T][N] ;
int m , n , ts ;
struct E{
int w ;
int v ;
} a [N] ;
void sc(){
m = read() , n = read() , ts = read() ;
for( int i = 1 ; i <= n ; i ++ ){
int k ;
a [i].w = read() ;
a [i].v = read() ;
k = read() ;
t [k][++ t [k][0]] = i ;
}
}
void work(){
for( int i = 1 ; i <= ts ; i ++ ){
for( int j = m ; j >= 0 ; j -- ){
for( int k = 1 ; k <= t [i][0] ; k ++ ){
if( j >= a [t [i][k]].w )
f [j] = max( f [j] , f [j - a [t [i][k]].w] + a [t [i][k]].v ) ;
}
}
}
printf( "%lld" , f [m] ) ;
}
signed main(){
sc() ;
work() ;
return 0 ;
}
7.依赖背包
问题
这种背包问题的物品间存在某种“依赖”的关系。也就是说,i依赖于j,表示若选物品i,则必须选物品j。依赖关系以图论中“森林”的形式给出(森林即多叉树的集合),也就是说,主件的附件仍然可以具有自己的附件集合,限制只是每个物品最多只依赖于一个物品(只有一个主件)且不出现循环依赖。
思路
解决这个问题仍然可以用将每个主件及其附件集合转化为物品组的方式。唯一不同的是,由于附件可能还有附件,就不能将每个附件都看作一个一般的01背包中的物品了。若这个附件也有附件集合,则它必定要被先转化为物品组,然后用分组的背包问题解出主件及其附件集合所对应的附件组中各个费用的附件所对应的价值。
事实上,这是一种树形DP,其特点是每个父节点都需要对它的各个儿子的属性进行一次DP以求得自己的相关属性。
具体见代码内注释
code
view code
#include<bits/stdc++.h>
#define int long long
using namespace std ;
inline int read(){
int w = 0 , f = 1 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) { if( ch == '-' ) f = -1 ; ch = getchar() ; }
while( ch >= '0' && ch <= '9' ){
w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ;
ch = getchar() ;
} return f * w ;
}
const int N = 2e2 + 10 ;
const int M = 2e2 + 10 ;
int f [N][N] ; // 第i个节点用j个空间的利益MAX
int n , m , v [M] , w [M] ;
int head [N] , cnt , root ;
struct E{ int to ; int next ;} a [2 * M] ;
void addi( int f , int t ){
a [cnt].to = t ;
a [cnt].next = head [f] ;
head [f] = cnt ++ ;
}
void sc(){
int p ; memset( head , -1 , sizeof( head ) ) ;
n = read() , m = read() ;
for( int i = 1 ; i <= n ; i ++ ){
v [i] = read() , w [i] = read() , p = read() ;
if( p == -1 ) root = i ;
else addi( p , i ) ;
}
}
void dfs( int t ){
for( int i = head [t] ; ~i ; i = a [i].next ){
int y = a [i].to ;
dfs( y ) ; //递归到达最底层
for( int j = m - v [t] ; j >= 0 ; j -- ){//给根节点留出他的空间(因为根节点必须选)
for( int k = 0 ; k <= j ; k ++ ){
f [t][j] = max( f [t][j] ,
f [t][j - k] + f [y][k]
) ;
// printf( "%lld %lld %lld \n" , t , j , f[t][j] ) ;
}
}
}for( int i = m ; i >= v [t] ; i -- ) f [t][i] = f [t][i - v [t]] + w [t] ;//选择根节点(必须选)
for( int i = 0 ; i < v [t] ; i ++ ) f [t][i] = 0 ;//他们无法选择根节点,根据依赖性,他们无法选择任何节点
}
void work(){
dfs( root ) ;
printf( "%lld" , f [root][m] ) ;
}
signed main(){
sc() ;
work() ;
return 0 ;
}
剩下两个我还不咋会,先咕着了
8.题目
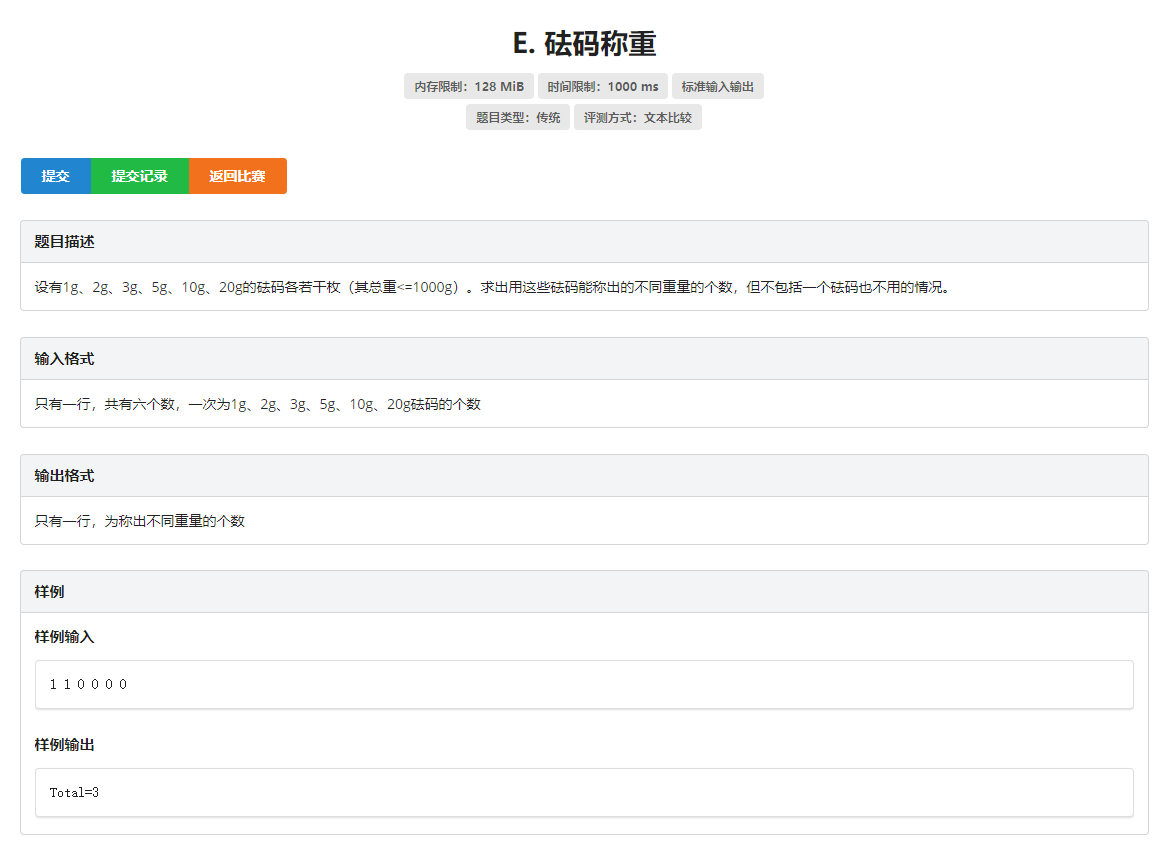
思路:这种算比较隐藏的背包问题,因为题目中并没有给出背包的体积。但是我们可以思考,对于每一个砝码都有选和不选两种状态,这本质上是一个01背包问题,只不过这个背包并不是把东西装到背包里面,而是把东西从背包中拿出来,看能出现多少种组合。所以我们正常推状态转移。一个状态是成立的,当且仅当他满足以下条件之一:
1.他不需要砝码(0g)/ 2.他由一个合法状态+已有砝码组成
所以我们把多重背包转化成01背包(本题数据水,暴力拆开和2进制拆开都可以)
然后枚举每一个砝码,对于每一个砝码,我们再枚举质量
code
view code
#include<bits/stdc++.h>
#define int long long
using namespace std ;
const int K = 7 ;
const int N = 1001 ;
vector<int> bag ;
bool fg [N] ;
int va [K] ;
inline int read(){
int w = 0 ; char ch = getchar() ;
while( ch >'9' || ch < '0' ) ch = getchar() ;
while( ch >= '0' && ch <= '9' ){
w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) ;
ch = getchar() ;
} return w ;
}
void sc(){
va [1] = 1 , va [2] = 2 , va [3] = 3 ;
va [4] = 5 , va [5] = 10 , va [6] = 20 ;
for( int i = 1 ; i <= 6 ; i ++ ){
int t = read() ;
for( int j = 1 ; j <= t ; j ++ )
bag.push_back( va [i] ) ;
}
}
void work(){
fg [0] = true ;
for( int i = 0 ; i < bag.size() ; i ++ )
for( int j = N ; j >= 0 ; j -- )
if( fg [j] )
fg [j + bag[i]] = true ;
int sum = 0 ;
for( int i = 1 ; i <= N ; i ++ )
if( fg [i] ) sum ++ ;
printf( "Total=%lld" , sum ) ;
}
signed main(){
sc() ;
work() ;
return 0 ;
}
2.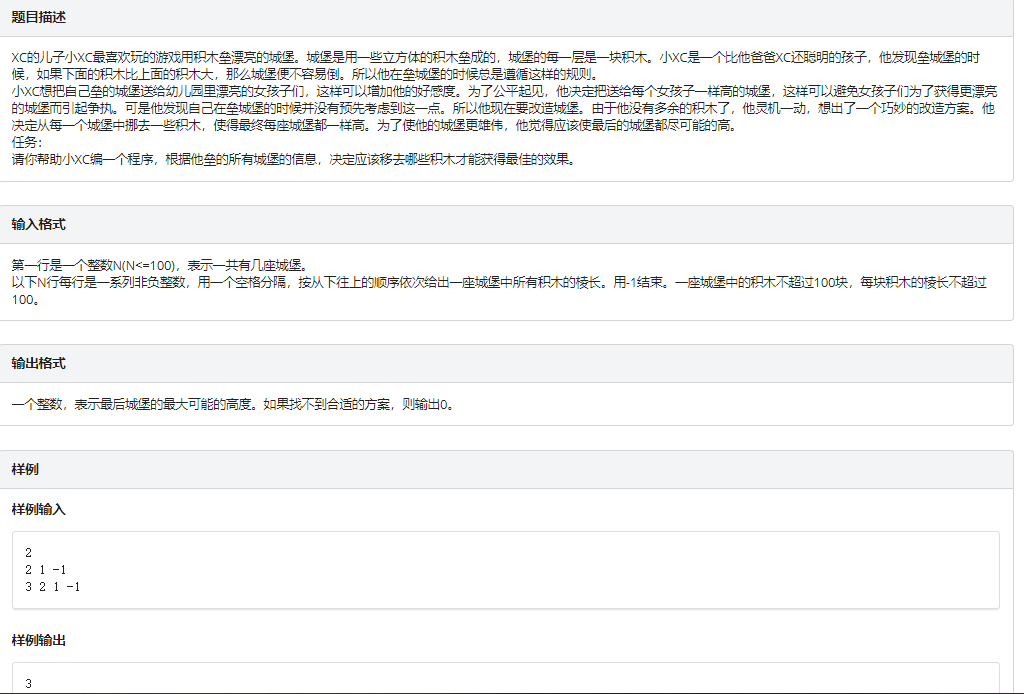
思路:其实这道题跟砝码一样,是一个把东西拿出来的背包dp,对于一座城堡来说,一个高度能被达到,当且仅当:
1.这个高度是0 / 2.这个高度由一个合法的高度和一块积木拼出
那么,这里运用一个小技巧,对于每座城堡,如果他能达到一个高度h,我们就把 \(ans[h]++\) , 最后从高到底枚举高度,如果ans[i] == n,则代表n个城堡都可以达到这个高度,直接输出退出循环即可
code
view code
#include<bits/stdc++.h>
#define R register int
#define int long long
using namespace std ;
const int N = 110 ;
const int M = 1e4 + 10 ;
inline int read(){
bool f = 0 ; w = 0 ; char ch = getchar() ;
while( ch < '0' || ch > '9' ) f |= ( ch == '-') , ch = getchar() ;
while( ch >= '0' && ch <= '9' ) w = ( w << 1 ) + ( w << 3 ) + ( ch - '0' ) , ch = getchar() ;
return f * w ;
}
int n ;
int len [N] ;
bool fg [M] ;
int ans [M] ;
void sc(){
n = read() ;
for( R is = 1 ; is <= n ; is ++ ){
memset( fg , 0 , sizeof( fg ) ) ; fg [0] = 1 ;
memset( len , 0 , sizeof( len ) ) ;
int m ; int i = 1 ;int h = 0 ;
while( i ){
m = read() ;
if( m == -1 ) break ;
len [i ++] = m ;
h += m ;
}
for( R j = 1 ; j < i ; j ++ ){
for( R k = h ; k >= len [j] ; k -- ){
fg [k] |= fg [k - len [j]] ;
}
}
for( R j = 1 ; j <= h ; j ++ )
if( fg [j] ) ans [j] ++ ;
}
for( R i = M ; i >= 1 ; i -- ){
if( ans [i] == n ) {
printf( "%lld\n" , i ) ;
return ;
}
}
printf( "0\n" ) ;
}
signed main(){
sc() ;
return 0 ;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号