题解 P2042 【[NOI2005] 维护数列】

P2042 [NOI2005] 维护数列

题目大意：

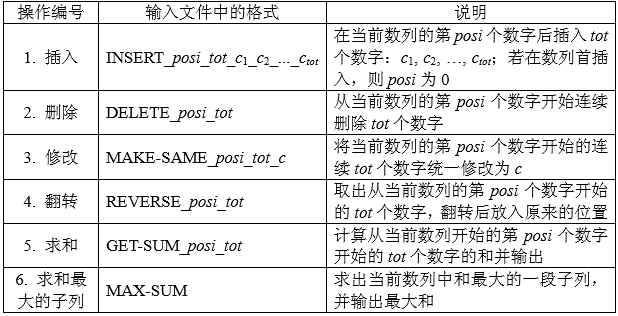
请写一个程序，要求维护一个数列，支持以下 \(6\) 种操作：

solution：

数据结构题，观察一下操作，看看要维护什么：

\(\text{Splay}\) 的基本信息：大小\(siz\)、父亲\(fa\)、值\(v\)、左右儿子\(s[\,2\,]\)。
懒标记：是否统一修改 \(sam\) 、是否翻转 \(rev\)。
维护操作 \(5\) 、\(6\) 的信息：区间和 \(sum\) 、区间最大子列和 \(mx\) 、区间最大前缀和 \(lx\) 、区间最大后缀和 \(rx\) 。

对于初始序列建树，我们有个小技巧 \(^1\)，后面讲。
对于每个操作，我们逐一击破：

插入：先找到 \(posi-1\) 数字的位置（在 \(\text{Splay}\) 中的编号）将其转到根，再将 \(posi+1\) 转到根的下面，这样 \(posi+1\) 的左子树就是要插入的位置。我们对插入的数列建一棵 \(\text{Splay}\) 然后接到 \(posi+1\) 的左儿子即可。
删除：找到区间左端点的前驱，将其转到根，将右端点的后继转到根下面，再将其左儿子清空即可。不过删除的点空间无法恢复，我们还有一个小技巧\(^2\)来节约空间，还是后面讲。
修改：同删除，将这段区间打个标记，同时更新一下这段区间的信息。
翻转：同修改。
求和：同删除，输出一下左儿子的 \(sum\) 即可。
求和最大子列：输出根节点的 \(mx\) 即可。

小技巧 \(^1\) ：

直接暴力插入会使 \(\text{Splay}\) 变成一条链，就不再平衡。我们可以参考线段树的建树方式每次选取区间的 \(mid\) 作为当前子树的根，\(l\) 到 \(mid-1\) 为其左子树，\(mid+1\) 到 \(r\) 为其右子树，在递归下去即可。

小技巧 \(^2\) ：

我们称它为回收站：把所有可用的节点编号存到 \(nodes\) 数组里，每需要一个就弹出，每删除一个就加入。在删除操作里，具体为通过 \(\text{dfs}\) 遍历出所有点，将其加入到 \(nodes\) 中。

细节处理：

思考两个区间操作的优先级，修改的优先级高于翻转，在 \(\text{pushdown}\) 时要注意下。
找一个 \(posi\) 的位置即查找排名为 \(posi\) 的数，注意哨兵对排名的影响。
注意 \(\text{pushup}\) 的顺序。

代码

#include<cstdio>
#include<algorithm>
#include<iostream>
using namespace std;
const int N=5e5+5,INF=1e9;
struct Splay{
	int s[2],siz,fa,v;
	int rev,sam;
	int sum,mx,lx,rx;
	inline void init(int _v,int _fa){
		s[0]=s[1]=0;
		siz=1,v=_v,fa=_fa;
		rev=sam=0;
		mx=sum=v,lx=rx=max(v,0);
	}
}tr[N];
int rt,nodes[N],cnt;
int a[N];
inline void pushup(int u){
	Splay &x=tr[u],&ls=tr[x.s[0]],&rs=tr[x.s[1]];
	x.siz=ls.siz+rs.siz+1;
	x.sum=ls.sum+rs.sum+x.v;
	x.lx=max(ls.lx,ls.sum+x.v+rs.lx);//同GSS系列的更新信息
	x.rx=max(rs.rx,rs.sum+x.v+ls.rx);
	x.mx=max(max(ls.mx,rs.mx),ls.rx+x.v+rs.lx);
}
inline void pushdown(int u){
	Splay &x=tr[u],&ls=tr[x.s[0]],&rs=tr[x.s[1]];//用了同样的技巧
	if(x.sam){//修改优先
		if(x.s[0]) ls.sam=1,ls.v=x.v,ls.sum=x.v*ls.siz;
		if(x.s[1]) rs.sam=1,rs.v=x.v,rs.sum=x.v*rs.siz;
		if(x.v>0){
			if(x.s[0]) ls.mx=ls.lx=ls.rx=ls.sum;
			if(x.s[1]) rs.mx=rs.lx=rs.rx=rs.sum;
		}
		else{
			if(x.s[0]) ls.mx=ls.v,ls.lx=ls.rx=0;
			if(x.s[1]) rs.mx=rs.v,rs.lx=rs.rx=0;
		}
		x.sam=x.rev=0;
	}
	else if(x.rev){
		ls.rev^=1,rs.rev^=1;
		swap(ls.lx,ls.rx),swap(rs.lx,rs.rx);
		swap(ls.s[0],ls.s[1]),swap(rs.s[0],rs.s[1]);
		x.rev=0;
	}
}
inline void rotate(int x){
	int y=tr[x].fa,z=tr[y].fa;
	int k=tr[y].s[1]==x;
	tr[z].s[tr[z].s[1]==y]=x,tr[x].fa=z;
	tr[y].s[k]=tr[x].s[k^1],tr[tr[x].s[k^1]].fa=y;
	tr[x].s[k^1]=y,tr[y].fa=x;
	pushup(y),pushup(x);
}
inline void splay(int x,int goal){
	while(tr[x].fa!=goal){
		int y=tr[x].fa,z=tr[y].fa;
		if(z!=goal)
			((tr[y].s[1]==x)^(tr[z].s[1]==y))?rotate(x):rotate(y);
		rotate(x);
	}
	if(!goal) rt=x;
}
inline int aval(int u,int k){//查询排名为 k 的数，返回的时 Splay 中的节点编号
	pushdown(u);
	if(tr[tr[u].s[0]].siz>=k)
		return aval(tr[u].s[0],k);
	if(tr[tr[u].s[0]].siz+1==k)
		return u;
	return aval(tr[u].s[1],k-tr[tr[u].s[0]].siz-1);
}
inline int build(int u,int l,int r){
	int mid=l+r>>1;
	int x=nodes[cnt--];
	tr[x].init(a[mid],u);
	if(l<mid) tr[x].s[0]=build(x,l,mid-1);
	if(r>mid) tr[x].s[1]=build(x,mid+1,r);
	pushup(x);
	return x;
}
inline void dfs(int u){
	if(tr[u].s[0]) dfs(tr[u].s[0]);
	if(tr[u].s[1]) dfs(tr[u].s[1]);
	nodes[++cnt]=u;
}
int main(){
	for(int i=1;i<N;i++) nodes[++cnt]=i;
	int n,m; scanf("%d%d",&n,&m);
	tr[0].mx=a[0]=a[n+1]=-INF;
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	rt=build(0,0,n+1);
	char op[10];
	int pos,tot;
	while(m--){
		scanf("%s",op);
		if(*op=='I'){
			scanf("%d%d",&pos,&tot);
			for(int i=1;i<=tot;i++)
				scanf("%d",&a[i]);
			int L=aval(rt,pos+1),R=aval(rt,pos+2);//找到左右的位置，因左端有哨兵，整体 pos 要 +1
			splay(L,0),splay(R,L);//转
			int u=build(R,1,tot);//将要添加的数列建成一棵 splay 
			tr[R].s[0]=u;//接上去
			pushup(R),pushup(L);
		}
		else if(*op=='D'){
			scanf("%d%d",&pos,&tot);
			int L=aval(rt,pos),R=aval(rt,pos+tot+1);//找到左右的位置
			splay(L,0),splay(R,L);//转
			dfs(tr[R].s[0]);//回收节点
			tr[R].s[0]=0;//清空左子树
			pushup(R),pushup(L);
		}
		else if(op[0]=='M'&&op[2]=='K'){
			int c; scanf("%d%d%d",&pos,&tot,&c);
			int L=aval(rt,pos),R=aval(rt,pos+tot+1);//找到左右的位置
			splay(L,0),splay(R,L);//转
			Splay &son=tr[tr[R].s[0]];//这里为了好些，取了地址，当 son 修改时 tr[tr[R].s[0]] 的信息也会修改，新学的小技巧。
			son.sam=1,son.v=c,
			son.sum=son.siz*c;//更新信息
			if(c>0) son.mx=son.lx=son.rx=son.sum;//若修改的数 >0 那么前缀后缀最大和都变为区间和
			else    son.mx=c,son.lx=son.rx=0;//否则都为0
			pushup(R),pushup(L);
		}
		else if(*op=='R'){
			scanf("%d%d",&pos,&tot);
			int L=aval(rt,pos),R=aval(rt,pos+tot+1);
			splay(L,0),splay(R,L);
			Splay &son=tr[tr[R].s[0]];
			son.rev^=1;
			swap(son.lx,son.rx);
			swap(son.s[0],son.s[1]);//同更新
			pushup(R),pushup(L);
		}
		else if(*op=='G'){
			scanf("%d%d",&pos,&tot);
			int L=aval(rt,pos),R=aval(rt,pos+tot+1);
			splay(L,0),splay(R,L);
			printf("%d\n",tr[tr[R].s[0]].sum);
		}
		else printf("%d\n",tr[rt].mx);//根节点的 mx 
	}
	return 0;
}

End

posted @ 2021-08-03 10:00 Mr_think 阅读(42) 评论(0) 收藏举报

刷新页面返回顶部

Mr_think

博学笃志，切问近思。