题解 UVA663【Sorting Slides】

UVA663 Sorting Slides

题目大意：

给定 \(n\) 个幻灯片\(A\) \(B\) \(C\) \(...\) 和对应编号 \(1\) ~ \(n\) ，以及幻灯片和编号的坐标。当编号在幻灯片内部时，编号和幻灯片可对应。求对应方案。若方案不唯一或无法对应，输出 none 。

solution:

一道二分图匹配题，当编号在幻灯片内部时，我们在该编号和幻灯片之间连一条边。都连完后跑二分图匹配模板，输出方案即可。

对方案不唯一的判定：我采用删边的方法，若删去这条边(即取消此编号与幻灯片的对应关系)后再匹配一边，若匹配数发生了变化，则该编号与该幻灯片对应关系唯一。否则不唯一。

正确性证明：

此图为连边后的二分图:

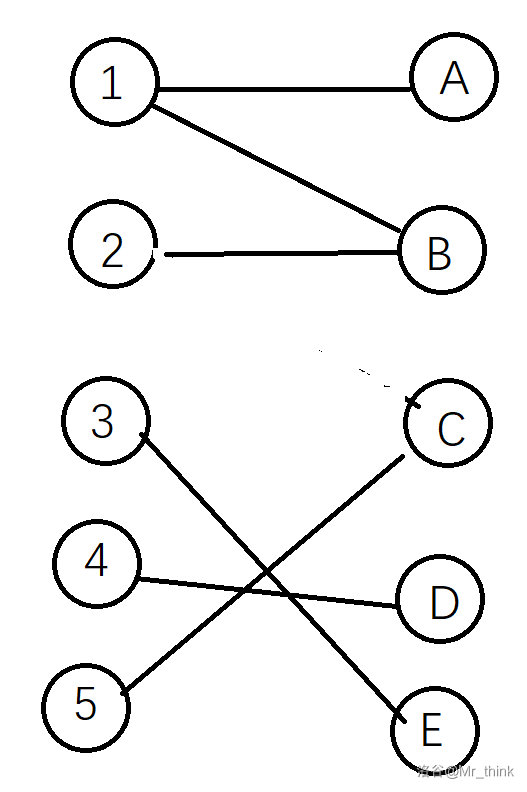
删去绿色的边仍为一个最大匹配则无唯一解：

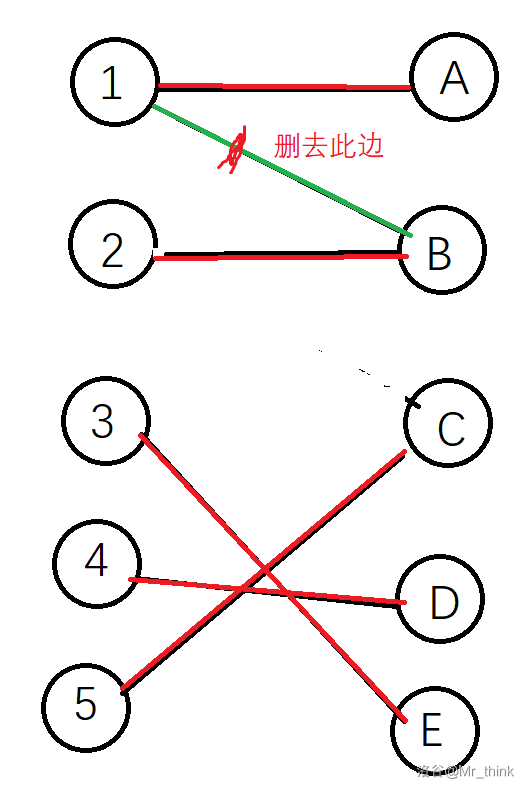
细节处理：

• \(\text{UVA}\) 是多组输入，注意初始化
• 删去的边要添回来
• 格式不注意，\(\text{WA}\) 两行泪！

看到这的同学，可以自己去写代码了(tf口吻)

代码

#include<cstdio>
#include<cstring>
using namespace std;
const int N=30;
int x1[N],y1[N],x2[N],y2[N];
int n;
bool g[N][N],vis[N];
int lian[N];
inline bool dfs(int x){
	for(int y=1;y<=n;y++){
		if(g[x][y]&&!vis[y]){
			vis[y]=1;
			if(!lian[y]||dfs(lian[y])){
				lian[y]=x;
				return 1;
			}
		}
	}
	return 0;
}
inline int pipei(){
	int sum=0;
	memset(lian,0,sizeof(lian));
	for(int x=1;x<=n;x++){
		memset(vis,0,sizeof(vis));
		if(dfs(x)) ++sum;
	}
	return sum;
}
int main(){
	int T=0;
	while(scanf("%d",&n)&&n){
		printf("Heap %d\n",++T);
		memset(g,0,sizeof(g));
		memset(lian,0,sizeof(lian));
		for(int i=1;i<=n;i++)
			scanf("%d%d%d%d",&x1[i],&x2[i],&y1[i],&y2[i]);
		for(int i=1,x,y;i<=n;i++){
			scanf("%d%d",&x,&y);
			for(int j=1;j<=n;j++)
				if(x>=x1[j]&&x<=x2[j]&&y>=y1[j]&&y<=y2[j])
					g[i][j]=1;
		}
		int ans=pipei(),flag=0;
		for(int y=1;y<=n;y++){
			for(int x=1;x<=n;x++){
				if(g[x][y]){
					g[x][y]=0;
					if(pipei()!=ans){
						if(flag) printf(" ");
						else flag=1;
						printf("(%c,%d)",y-1+'A',x);
					}
					g[x][y]=1;
				}
			}
		}
		if(!flag) printf("none");
		printf("\n\n");
	}
	return 0;
}

End