题解 UVA11987 【Almost Union-Find】

UVA11987 Almost Union-Find

题目大意

现有 \(n\) 个集合 \(m\) 个操作。规定第 \(i\) 个集合里为 \(\{i\}\) 。操作包括：

1. 输入两个元素 p 、 q ，如果 p 、q 不在一个集合中，合并这两个元素所在的集合。
2. 输入两个元素 p 、 q ，如果 p 、q 不在一个集合中，将 p 添到 q 所在的集合。
3. 输入一个元素 p ，查询 p 所在的集合的大小和元素和。

solution:

看到集合，考虑使用并查集 (冰茶姬) ， 1 和 3 操作都很容易实现，难点在于操作 2 。我们并不可以通过

fa[p]=cha(q);//cha()函数返回q所在集合的根节点

直接将 p 添加到 q 所在的集合。举个反例：

现在集合的状态如上图，如果此时有 2 1 3 ，按照上面的语句就变成了这样：

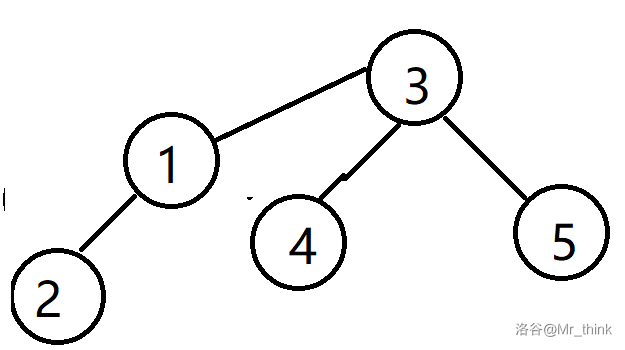
我们会发现，此时元素 2 也被添加到了集合中，是不允许的。分析一下原因，源赖氏由于 1 为根节点才出错。考虑解决：我们可以添加一个虚拟根节点，编号为 \(i+n\) ，现在我们再看这个过程：

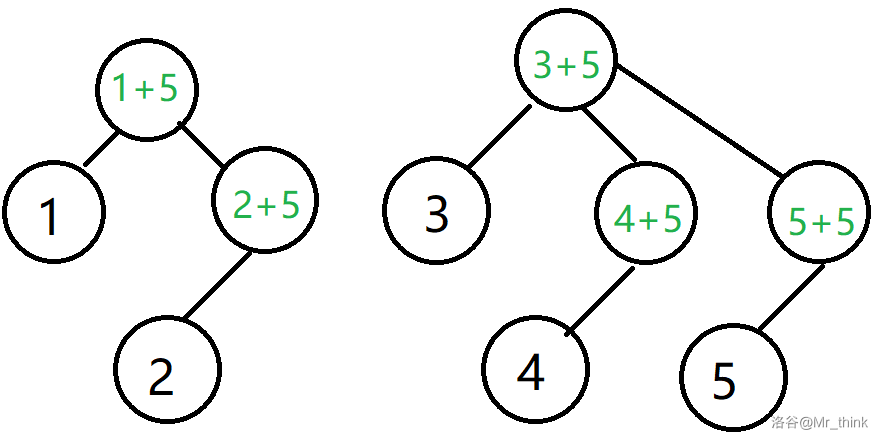
经过上述操作后：

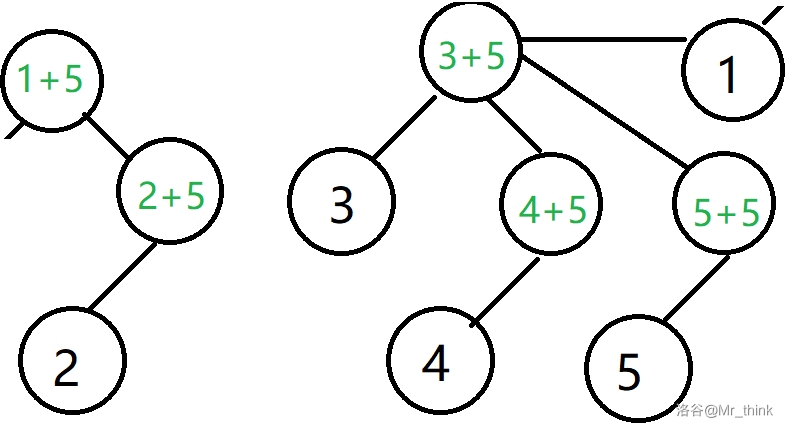
噫，好了！符合题意。

接下来是细节的处理：

1. 由于我们建立了虚拟根节点，所以要开二倍的空间。
2. \(\text{UVA}\) 是多组输入，要

while(scanf("%d%d",&n,&m)!=EOF)

看到这的同学，可以自己去写代码了(tf口吻)

代码

#include<cstdio>
using namespace std;
const int N=100005;
int fa[N*2],he[N*2],shu[N*2];
int n,m;
inline void chu()
{
	for(int i=1;i<=n;i++)
		fa[i]=i+n,fa[i+n]=i+n,he[i+n]=i,shu[i+n]=1;
}
int cha(int s){	return fa[s]==s?s:fa[s]=cha(fa[s]);}
inline void bing(int a,int b)
{
	int ba=cha(a),bb=cha(b);
	if(ba!=bb) 
	{
		fa[ba]=bb,
		he[bb]+=he[ba],
		shu[bb]+=shu[ba];
	}
}
inline void yi(int a,int b)
{
	int ba=cha(a),bb=cha(b);
	if(ba!=bb)
	{
		fa[a]=bb;
		he[ba]-=a,he[bb]+=a;
		shu[ba]--,shu[bb]++;
	}
}
inline void sum(int s)
{
	int ba=cha(s);
	printf("%d %d\n",shu[ba],he[ba]);
}
int main()
{
	while(scanf("%d%d",&n,&m)!=EOF)
	{
		chu();
		while(m--)
		{
			int op,p,q;
			scanf("%d%d",&op,&p);
			if(op==1)
			{
				scanf("%d",&q);
				bing(p,q);
			}
			else if(op==2)
			{
				scanf("%d",&q);
				yi(p,q);
			}
			else sum(p);
		}
	}
	return 0;
}

End