题解 CF938D Buy a Ticket

CF938D Buy a Ticket

题目大意：

有一个乐队要开演唱会，在 \(n\) 个城市的人都想去听，但每个城市票价不同，而他们都想少花钱。给定 \(m\) 条路，包含 \(u\), \(v\), \(w\) 表示从城市 \(u\) 到城市 \(v\) 要花 \(w\) 元，再给出演唱会在 \(i\) 城市的票价 \(a[i]\)，求每个人去听演唱会并回来的最小花费。

solution:

暴力地去想，我们可以从 \(i\) 出发求到城市 \(j\) 的最短路加上城市 \(j\) 的票价 \(a[i]\) 取一个 \(\min\) 就可以求出此人的最小花费，时间复杂度爆炸 \(O(n\times(n+m)\log n)\)（ \(\text{Dijkstra}\) 堆优化）。当然我们也可以用 \(\text{Floyd}\ O(N^3)\)。

考虑优化：思考一下时间耗费在哪里了。我们发现在跑最短路时是不能确定终点的，最后还要通过加上最后城市的票价 \(a[i]\) 才可以确定最小值。如果将演唱会的票价放到最短路里跑一边不就行了？这样一来，就可以直接求出最小花费。所以我们化点权为边权，建立一个虚拟源点—— \(0\) 号节点，向其他城市 \(i\) 连一条边权为 \(a[i]\) 的边。

如图所示(样例一)：

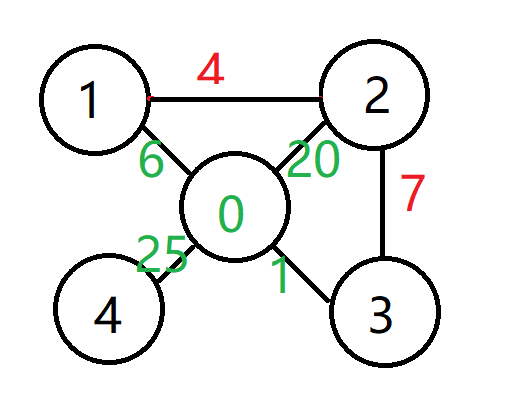
这样，我们每次从 \(0\) 号节点作为起点跑最短路，就可以求出最小花费了。

正确性证明：

从 \(0\) 号节点到 \(i\) 的最短路径，必然存在且只存在一条从 \(0\) 号节点连向城市 \(j\) 的边，经过此边即代表去此城市听演唱会。

接下来是细节的处理：

1. 看了一眼数据范围 \(1\le a_i,w_i\le 10^{12}\) 果断开 \(\texttt{long long}\)
2. 注意要往返，所以连边是边权为 \(2\times w_i\)
3. 边数要开三倍(无向图+虚拟源点连的边)

同类题推荐[P7100 [w3R1] 团]

看到这的同学，可以自己去写代码了(tf口吻)

代码

#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;
const int N=200005;
typedef pair<long long,long long> PLL;
typedef long long LL;
bool vis[N];
LL hd[N],nt[N*3],e[N*3],w[N*3],dis[N];
LL  cnt=0;
priority_queue< PLL,vector<PLL>,greater<PLL> > Q;
void tian(LL a,LL b,LL c)
{
	e[++cnt]=b;
	w[cnt]=c;
	nt[cnt]=hd[a];
	hd[a]=cnt;
}
int main()
{
	memset(dis,0x3f,sizeof(dis));
	LL n,m;
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=m;i++)
	{
		LL x,y,z;
		scanf("%lld%lld%lld",&x,&y,&z);
		tian(x,y,2*z),tian(y,x,2*z);
	}
	for(int i=1;i<=n;i++)
	{
		LL p;
		scanf("%lld",&p);
		tian(0,i,p);
	}
	dis[0]=0;
	Q.push(make_pair(0,0));
	while(Q.size())
	{
		int wei=Q.top().second;
		Q.pop();
		if(vis[wei]) continue;
		vis[wei]=1;
		for(int i=hd[wei];i;i=nt[i])
		{
			int dian=e[i];
			if(dis[wei]+w[i]<dis[dian])
			{
				dis[dian]=dis[wei]+w[i];
				Q.push(make_pair(dis[dian],dian));
			}
		}
	}
	for(int i=1;i<=n;i++)
		printf("%lld ",dis[i]);
}

End