题解 P7100 【[w3R1] 团】

P7100 [w3R1] 团

题目大意：

有一个\(n\)个节点的无向带权图，由\(k\)个集合组成，每个集合\(S_i\)中有一些点\(\lbrace(T_1,W_1),(T_2,W_2),...,(T_{\left|S_i\right|},W_{\left|S_i\right|})\rbrace\)，集合中的任意两点都有一条连接\(T_i,T_j\)的无向边，边权为\(W_i+W_j\)。我们要求 \(1\) 到 \(i\) 的最短路。

solution:

tf老师说：“图论题，建完图后打个模板就行了。”，所以我们考虑如何建图。

暴力地去想，对于每个集合中的点\(T_i\)，我们可以从\(T_i\)向其他点\(T_j\)连一条边。
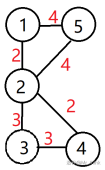
根据样例建图如下图：

时间复杂度爆炸：\(O(k|S_i^2|)\)

所以我们考虑，在每个集合中新添一个虚拟节点\(T_{n+i}\)，其点权\(W_{i+n}\)为0，再向其他点\(T_j\)连边。
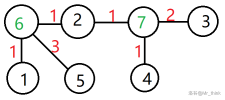
如下图：

时间复杂度：\(O(k|S_i|)\)

正确性证明：

我们举个例子，原图中\(3\rightarrow4\)的路径被拆成了\(3\rightarrow7\rightarrow4\)，边权和仍为\(3\)。我们这个过程的实质就是将一条边拆成两条边。

接下来，我们打上最短路模板 \(\text{dijkstra}\) 堆优化或者\(\text{SPFA}\)均可通过此题。

细节处理：

总路径长有可能超\(\text{int}\)，所以要开\(\text{long}\) \(\text{long}\)。\(dis\)数组要初始化成\(\text{0x3f3f3f3f3f3f3f3f}\)

看到这的同学，可以自己去写代码了(tf口吻)

代码

``` cpp #include #include #include using namespace std; typedef long long LL; const int M=800002; int hd[M],nt[M],e[M],ww[M],num=0; bool vis[M]; LL dis[M],INF=0x3f3f3f3f3f3f3f3f; queue Q; void tian(int a,int b,int c) { e[++num]=b; ww[num]=c; nt[num]=hd[a]; hd[a]=num; } void qing() { memset(hd,-1,sizeof(hd)); memset(vis,0,sizeof(vis)); memset(dis,0x3f,sizeof(dis)); } int main() { qing(); int n,k; scanf("%d%d",&n,&k); int ew=n; for(int i=1;i<=k;i++) { int s; scanf("%d",&s); for(int j=1;j<=s;j++) { int t,w; scanf("%d%d",&t,&w); tian(t,ew+i,w);tian(ew+i,t,w); } } dis[1]=0; vis[1]=1; Q.push(1); while(Q.size()) { int x=Q.front(); Q.pop(); vis[x]=0; for(int i=hd[x];i!=-1;i=nt[i]) { int y=e[i],z=ww[i]; if(dis[y]>dis[x]+z) { dis[y]=dis[x]+z; if(!vis[y]) { Q.push(y); vis[y]=1; } } } } for(int i=1;i<=n;i++) printf("%lld ",dis[i]); return 0; } ```

End