分块

分块的本质是优化的暴力~~~

本人是个蒟蒻/菜鸡/小辣鸡, 目前只搞懂了普通的分块, 至于值域分块和操作分块等还在路上...持续更新!

普通分块

思想

其实我觉得分块最主要的就是思想

问题引入

给你一个大小为 $n$ 的序列 $a[1],a[2]...a[n]$.要求支持区间修改以及查询区间和(洛谷 P2357 守墓人).~~(反正我是把这道题当作分块入门的)~~

解决

已经学了线段树的我们第一反应当然是用线段树去维护区间信息了,但是我们是来学分块的!~~不忘初心,牢记使命~~所以,我们要用分块的思想来$A$了这道题.

首先,分块既然是优化暴力, 那我们先来考虑暴力的写法.~~还用想吗?~~
明显,区间修改和区间查询都是直接暴力左端点到右端点. 那么, 我们可以考虑标记这个区间, 在整个区间段上打上懒标记. 但是我们的修改并不是固定的, 如果每次修改查询左右端点都不重复, 那就没用了. 于是, 我们可以考虑固定我们所要分的区间, 即把原数组分成一个一个块. 这就是分块了. 分块的思想就是将原数组分成一个一个块, 每次修改/查询的时候对于在操作区间内的完整的块, 可以直接暴力给每个块打上懒标记. 对于整块两段的元素(散块), 单独暴力. 过程如图:

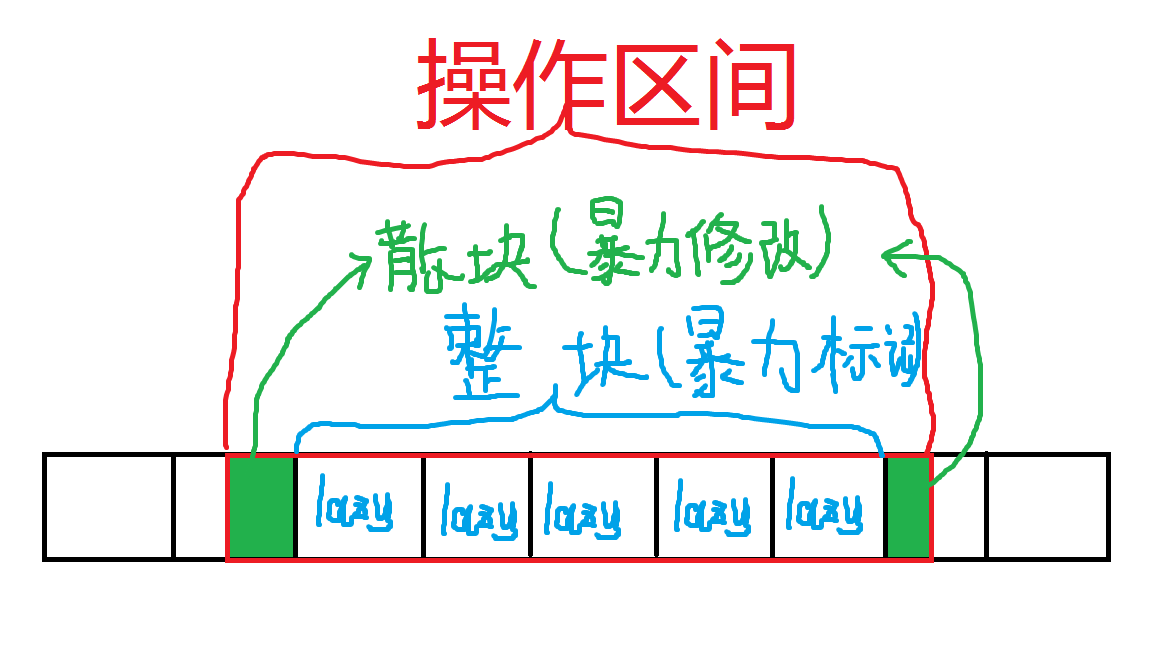
实现

首先要考虑块的大小. 如果块很大, 那么散块部分的暴力复杂度将会非常大. 同理, 若块太小, 那整块的处理复杂度也会非常大. (本质上最朴素的暴力就是块的大小为 $1$ $or$ 为 $n$ 的时候.) 所以, 最好的效率应是 $sqrt(n)$. 但是以上的结论是在询问区间的长度随机均匀的前提下. 如果题目有特殊限制, 那么块的最佳大小应有相应的改变(比如, 在询问的区间长度已知都非常大时, 块的大小应稍微大一些).

在考虑完块长后, 其他的都很好考虑了. 我们只要记下每个块内的信息, 懒标记, 左右端点, 以及每个元素分别在哪一个块内(我的数组名为$in[i]$).

一开始, 预处理出每个块的初始信息即可($O(n)$).

该模板题的代码

第一次打,相当丑.~~虽然我码风一直都很丑, 但是改不掉了啊. 唉...~~

#include<cstdio>
#include<cmath>
#define Maxn 200000
#define Maxs 1000
#define int long long
using namespace std;
int read() {
	int f = 1, sum = 0;
	char ch = getchar();
	while(ch < '0' || ch > '9') {
		if(ch == '-') f = -1;
		ch = getchar();
	}
	while(ch >= '0' && ch <= '9') {
		sum = sum * 10 + ch - '0';
		ch = getchar();
	}
	return f * sum;
}
void write(int x) {
	(x < 0) ? (putchar('-'), write(-x)) : (void)((x <= 9) ? (putchar(x + '0')) : (write(x / 10), putchar(x % 10 + '0')));
}
int n, T, a[Maxn + 9], Base, s, in[Maxn + 9], xh[Maxn + 9];
struct BLOCK {
	int val, lazy, cnt, num[Maxs + 9];
} S[Maxs + 9];
void Swap(int &a, int &b) {
	int t = a;
	a = b;
	b = t;
}
void Update(int l, int r, int k) {
	if(l > r) Swap(l, r);
	if(in[l] == in[r]) {
		S[in[l]].val += (r - l + 1) * k;
		for(int i = xh[l]; i <= xh[r]; ++i) {
			S[in[l]].num[i] += k;
		}
	}
	else {
		S[in[l]].val += (S[in[l]].cnt - xh[l] + 1) * k;
		for(int i = xh[l]; i <= S[in[l]].cnt; ++i) {
			S[in[l]].num[i] += k;
		}
		S[in[r]].val += xh[r] * k;
		for(int i = 1; i <= xh[r]; ++i) {
			S[in[r]].num[i] += k;
		}
		for(int i = in[l] + 1; i < in[r]; ++i) {
			S[i].val += S[i].cnt * k;
			S[i].lazy += k;
		}
	}
}
int Query(int l, int r) {
	if(l > r) Swap(l, r);
	int ans = 0;
	if(in[l] == in[r]) {
		for(int i = xh[l]; i <= xh[r]; ++i) {
			ans += S[in[l]].num[i] + S[in[l]].lazy;
		}
	}
	else {
		ans += (S[in[l]].cnt - xh[l] + 1) * S[in[l]].lazy;
		for(int i = xh[l]; i <= S[in[l]].cnt; ++i) {
			ans += S[in[l]].num[i];
		}
		ans += xh[r] * S[in[r]].lazy;
		for(int i = 1; i <= xh[r]; ++i) {
			ans += S[in[r]].num[i];
		}
		for(int i = in[l] + 1; i < in[r]; ++i) {
			ans += S[i].val;
		}
	}
	return ans;
}
void Solve() {
	int opt = read();
	if(opt == 1) {
		int l = read(), r = read(), k = read();
		Update(l, r, k);
	}
	else if(opt == 2) {
		int k = read();
		Update(1, 1, k);
	}
	else if(opt == 3) {
		int k = read();
		Update(1, 1, -k);
	}
	else if(opt == 4) {
		int l = read(), r = read();
		write(Query(l, r));
		putchar('\n');
	}
	else {
		write(Query(1, 1));
		putchar('\n');
	}
}
signed main() {
	n = read(), T = read();
	for(int i = 1; i <= n; ++i) {
		a[i] = read();
	}
	Base = sqrt(n), s = n / Base;
	for(int i = 1; i <= s; ++i) {
		for(int j = 1; j <= Base; ++j) {
			S[i].val += a[(i - 1) * Base + j];
			in[(i - 1) * Base + j] = i;
			xh[(i - 1) * Base + j] = j;
			S[i].num[++S[i].cnt] = a[(i - 1) * Base + j];
		}
	}
	if(s * Base != n) {
		++s;
		for(int i = n / Base * Base + 1; i <= n; ++i) {
			S[s].val += a[i];
			in[i] = s;
			xh[i] = i - n / Base * Base;
			S[s].num[++S[s].cnt] = a[i];
		}
	}
	while(T--) {
		Solve();
	}
	return 0;
}

然而, 由于最基本的分块太简单, 所以一般都要加上一些奇奇怪怪的预处理或者块内处理. 下面来分析几道例题.

例题1(洛谷 P3203 [HNOI2010]弹飞绵羊)

~~我从未见过如此水的紫题(逃)~~

首先像普通分块那样分成 $sqrt(n)$ 个大小也为 $sqrt(n)$ 的块. 然后再预处理出从当前点开始, 需要几步才能弹出当前块, 以及弹到了哪个位置. 这样的话, 修改时最多$sqrt(n)$, 因为当前块内的影响对后面的块并无影响. 查询也是 $sqrt(n)$ 的, 因为在我们的处理下, 从一个块到另一个块的复杂度已经变成$O(1)$的了.

其实我觉得这道题更能印证分块就是优化的暴力

#include<cstdio>
#include<cmath>
#define Maxn 200000
#define Maxs 500
using namespace std;
int read() {
	int f = 1, sum = 0;
	char ch = getchar();
	while(ch < '0' || ch > '9') {
		if(ch == '-') f = -1;
		ch = getchar();
	}
	while(ch >= '0' && ch <= '9') {
		sum = sum * 10 + ch - '0';
		ch = getchar();
	}
	return f * sum;
}
void write(int x) {
	(x < 0) ? (putchar('-'), write(-x)) : (void)((x <= 9) ? (putchar(x + '0')) : (write(x / 10), putchar(x % 10 + '0')));
}
int n, k[Maxn + 9], in[Maxn + 9];
struct BLOCK {
	int l, r;
} b[Maxs + 9];
struct FLY_OUT {
	int nd, id;
} fly_out[Maxn + 9];
int min(int x, int y) {
	return x < y ? x : y;
}
int Query(int x) {
	int ans = 0;
	while(x <= n) {
		ans += fly_out[x].nd;
		x = fly_out[x].id;
	}
	return ans;
}
void Update(int x, int nk) {
	int id = in[x];
	k[x] = nk;
	for(int j = x; j >= b[id].l; --j) 
		if(j + k[j] > b[id].r) fly_out[j].nd = 1, fly_out[j].id = j + k[j];
		else fly_out[j].id = fly_out[j + k[j]].id, fly_out[j].nd = fly_out[j + k[j]].nd + 1;
}
void Solve() {
	int opt = read();
	if(opt == 1) {
		int x = read() + 1;
		write(Query(x));
		putchar('\n');
	}
	else {
		int x = read() + 1, nk = read();
		Update(x, nk);
	}
}
signed main() {
	n = read();
	int Base = sqrt(1.0 * n), S = ceil(1.0 * n / Base);
	for(int i = 1; i <= n; ++i) {
		k[i] = read();
		in[i] = (i - 1) / Base + 1;
	}
	for(int i = 1; i <= S; ++i) {
		b[i].l = (i - 1) * Base + 1, b[i].r = min(n, i * Base);
		for(int j = b[i].r; j >= b[i].l; --j) {
			if(j + k[j] > b[i].r) fly_out[j].nd = 1, fly_out[j].id = j + k[j];
			else fly_out[j].id = fly_out[j + k[j]].id, fly_out[j].nd = fly_out[j + k[j]].nd + 1;
		}
	}
	int T = read();
	while(T--) {
		Solve();
	}
	return 0;
}

例题2(洛谷 P3793 由乃救爷爷)

神奇的问题: 为什么上上道区间和是黄题, 然而这道题却变成了蓝的???(而且本题还不带修)

看数据范围.

这就需要我们做一下块与块之间的预处理. 我们用 $ans[i][j]$ 表示第$i$块到第$j$块间的最大值. 对此, 我们可以在此前 $O(n)$ 预处理出每块内的最大值, 再暴力$i$和$j$, 由于只有$sqrt(n)$ 个块, 所以此次暴力是$O(n)$的.

你以为这样就可以了吗? 大错特错!

我们还要预处理出从当前点到其所在块的左端点和右端点之间的最大值. 这个在第一次预处理时即可完成.

这样, 除了查询在一个块内的时候需要暴力, 其余的查询都是$O(1)$ 的.平均下来每次查询是比$sqrt(n)$要小的.

#include<bits/stdc++.h>
#define Maxn 20000000
#define Maxs 5000
using namespace std;
namespace GenHelper
{
    unsigned z1,z2,z3,z4,b;
    unsigned rand_()
    {
    b=((z1<<6)^z1)>>13;
    z1=((z1&4294967294U)<<18)^b;
    b=((z2<<2)^z2)>>27;
    z2=((z2&4294967288U)<<2)^b;
    b=((z3<<13)^z3)>>21;
    z3=((z3&4294967280U)<<7)^b;
    b=((z4<<3)^z4)>>12;
    z4=((z4&4294967168U)<<13)^b;
    return (z1^z2^z3^z4);
    }
}
void srand(unsigned x)
{using namespace GenHelper;
z1=x; z2=(~x)^0x233333333U; z3=x^0x1234598766U; z4=(~x)+51;}
int read()
{
    using namespace GenHelper;
    int a=rand_()&32767;
    int b=rand_()&32767;
    return a*32768+b;
}
int a[Maxn + 9], f[Maxs + 9][Maxs + 9], in[Maxn + 9];
int lm[Maxn + 9], rm[Maxn + 9];
unsigned long long ans;
struct BLOCK {
	int l, r;
} bl[Maxs + 9];
signed main() {
	int n, m, s;
	scanf("%d%d%d", &n, &m, &s);
	srand(s);
	int Base = sqrt(n), S = ceil(1.0 * n / Base);
	for(int i = 1; i <= n; ++i) {
		a[i] = read();
		in[i] = (i - 1) / Base + 1;
	}
	for(int i = 1; i <= S; ++i) {
		bl[i].l = (i - 1) * Base + 1, bl[i].r = min(n, i * Base);
	}
	
	for(int i = 1; i <= S; ++i) {
		lm[bl[i].l] = a[bl[i].l], rm[bl[i].r] = a[bl[i].r];
		for(int j = bl[i].l + 1; j <= bl[i].r; ++j) {
			lm[j] = max(lm[j - 1], a[j]);
		}
		for(int j = bl[i].r - 1; j >= bl[i].l; --j) {
			rm[j] = max(rm[j + 1], a[j]);
		}
	}
	
	for(int i = 1; i <= S; ++i) {
		f[i][i] = lm[bl[i].r];
		for(int j = i + 1; j <= S; ++j) {
			f[i][j] = max(f[i][j - 1], lm[bl[j].r]);
		}
	}
	while(m--) {
		int l = read() % n + 1, r = read() % n + 1;
		if(l > r) swap(l, r);
		if(in[l] == in[r]) {
			int mx = a[l];
			for(int i = l + 1; i <= r; ++i) {
				mx = max(mx, a[i]);
			}
			ans += (unsigned long long)mx;
			continue;
		}
		int mx = max(rm[l], lm[r]);
		if(in[l] + 1 == in[r]) {
			ans += (unsigned long long)mx;
			continue;
		}
		mx = max(mx, f[in[l] + 1][in[r] - 1]);
		ans += (unsigned long long)mx;
	}
	printf("%llu", ans);
	return 0;
}

例题3(洛谷 P5356 [Ynoi2017] 由乃打扑克)

这道题其实难得就是想到块内排序+二分答案. 其余的就是码量稍微有点大.~~(讲真的, 代码调起来超级烦的)~~

还有个重点, 由乃$OI$是少不了卡常的.

#include<cstdio>
#include<cmath>
#include<algorithm>
#define Maxn 100000
#define Maxs 100000
using namespace std;
int read() {
	int f = 1, sum = 0;
	char ch = getchar();
	while(ch < '0' || ch > '9') {
		if(ch == '-') f = -1;
		ch = getchar();
	}
	while(ch >= '0' && ch <= '9') {
		sum = sum * 10 + ch - '0';
		ch = getchar();
	}
	return f * sum;
}
void write(int x) {
	(x < 0) ? (putchar('-'), write(-x)) : (void)((x <= 9) ? (putchar(x + '0')) : (write(x / 10), putchar(x % 10 + '0')));
}
int n, in[Maxn + 9], mrg1, mrg2;
struct A {
	int num, id;
} a[Maxn + 9], mg1[Maxs + 9], mg2[Maxn + 9];
struct BLOCK {
	int lazy, l, r;
} bl[Maxs + 9];
void Swap(int &a, int &b) {
	int t = a;
	a = b;
	b = t;
}
bool CmpNum(A x, A y) {
	return x.num < y.num;
}
int min(int x, int y) {
	return x < y ? x : y;
}
int max(int x, int y) {
	return x > y ? x : y;
}
int tmp1[Maxn + 9], tmpp1, tmp2[Maxn + 9], tmpp2, tmp3[Maxn + 9], tmpp3;
int Sum(int l ,int r, int k) {
	int left = 1, right = tmpp3, mid, sum = 0;
	while(left <= right) {
		mid = left + right >> 1;
		if(tmp3[mid] > k) right = mid - 1;
		else left = mid + 1;
	}
	sum += right;
	for(int i = in[l] + 1; i <= in[r] - 1; ++i) {
		left = bl[i].l, right = bl[i].r;
		while(left <= right) {
			mid = left + right >> 1;
			if(a[mid].num + bl[i].lazy > k) right = mid - 1;
			else left = mid + 1;
		}
		sum += right - bl[i].l + 1;
	}
	return sum;
}
int Query(int l, int r, int k) {
	if((r - l + 1) < k || k < 1) return -1;
	if(in[l] == in[r]) {
		tmpp3 = 0;
		for(int i = bl[in[l]].l; i <= bl[in[l]].r; ++i) {
			if(a[i].id >= l && a[i].id <= r) {
				tmp3[++tmpp3] = a[i].num;
			}
		}
		return tmp3[k] + bl[in[l]].lazy;
	}
	tmpp1 = tmpp2 = tmpp3 = 0;
	for(int i = bl[in[l]].l; i <= bl[in[l]].r; ++i) {
		if(a[i].id >= l) tmp1[++tmpp1] = a[i].num + bl[in[l]].lazy;
	}
	for(int i = bl[in[r]].l; i <= bl[in[r]].r; ++i) {
		if(a[i].id <= r) tmp2[++tmpp2] = a[i].num + bl[in[r]].lazy;
	}
	int p1 = 1, p2 = 1;
	while(p1 <= tmpp1 && p2 <= tmpp2) {
		if(tmp1[p1] < tmp2[p2]) tmp3[++tmpp3] = tmp1[p1++];
		else tmp3[++tmpp3] = tmp2[p2++];
	}
	while(p1 <= tmpp1) tmp3[++tmpp3] = tmp1[p1++];
	while(p2 <= tmpp2) tmp3[++tmpp3] = tmp2[p2++];
	if(in[l] + 1 == in[r]) return tmp3[k];
	int L = tmp3[1], R = tmp3[tmpp3];
	for(int i = in[l] + 1; i <= in[r] - 1; ++i) {
		L = min(L, a[bl[i].l].num + bl[i].lazy);
		R = max(R, a[bl[i].r].num + bl[i].lazy);
	}
	if(k == (r - l + 1)) return R;
	if(k == 1) return L;
	int mid, ttttt = -1;
	while(L <= R) {
		mid = L + R >> 1;
		if(Sum(l, r, mid) < k) L = mid + 1;
		else ttttt = mid, R = mid - 1;
	}
	return ttttt;
}
void Merge(int l, int r) {
	int p1 = 1, p2 = 1, p3 = 0;
	while(p1 <= mrg1 && p2 <= mrg2) {
		if(mg1[p1].num < mg2[p2].num) a[l + p3] = mg1[p1++];
		else a[l + p3] = mg2[p2++];
		++p3;
	}
	while(p1 <= mrg1) {
		a[l + p3] = mg1[p1++];
		++p3;
	}
	while(p2 <= mrg2) {
		a[l + p3] = mg2[p2++];
		++p3;
	}
}
void Update(int l, int r, int k) {
	if(in[l] == in[r]) {
		mrg1 = mrg2 = 0;
		for(int i = bl[in[l]].l; i <= bl[in[l]].r; ++i) {
			if(a[i].id >= l && a[i].id <= r) {
				mg1[++mrg1] = a[i];
				mg1[mrg1].num += k;
			} else {
				mg2[++mrg2] = a[i];
			}
		}
		Merge(bl[in[l]].l, bl[in[l]].r);
	} else {
		mrg1 = mrg2 = 0;
		for(int i = bl[in[l]].l; i <= bl[in[l]].r; ++i) {
			if(a[i].id >= l && a[i].id <= bl[in[l]].r) {
				mg1[++mrg1] = a[i];
				mg1[mrg1].num += k;
			} else {
				mg2[++mrg2] = a[i];
			}
		}
		Merge(bl[in[l]].l, bl[in[l]].r);
		mrg1 = mrg2 = 0;
		for(int i = bl[in[r]].l; i <= bl[in[r]].r; ++i) {
			if(a[i].id >= bl[in[r]].l && a[i].id <= r) {
				mg1[++mrg1] = a[i];
				mg1[mrg1].num += k;
			} else {
				mg2[++mrg2] = a[i];
			}
		}
		Merge(bl[in[r]].l, bl[in[r]].r);
		for(int i = in[l] + 1; i <= in[r] - 1; ++i) {
			bl[i].lazy += k;
		}
	}
}
void Solve() {
	int opt = read(), l = read(), r = read(), k = read();
	if(opt == 1) {
		write(Query(l, r, k));
		putchar('\n');
	} else {
		Update(l, r, k);
	}
}
signed main() {
	int T;
	n = read(), T = read();
	int Base;
	if(n == 1) Base = 1;
	else Base = 678;
	int S = ceil(1.0 * n  / Base);
	for(int i = 1; i <= S; ++i) {
		bl[i].l = (i - 1) * Base + 1, bl[i].r = min(n, i * Base);
		for(int j = bl[i].l; j <= bl[i].r; ++j) {
			a[j].num = read();
			a[j].id = j;
			in[j] = i;
		}
		sort(a + bl[i].l, a + bl[i].r + 1, CmpNum);
	}
	while(T--) {
		Solve();
	}
	return 0;
}

例题4(洛谷 [Ynoi2019 模拟赛] Yuno loves sqrt technology I)

本题又来自于由乃$OI$, 卡常卡得我身心俱疲(逃).

首先这道题是不带修的, 所以我们可以把大部分答案都预处理出来. 具体地, 我们需要预处理的数据有:

$pre[i]$___表示下标为$i$的位置到它所在的块的左端点之间的逆序对数(用树状数组做$O(nlogn)$).
$suf[i]$___表示下标为$i$的位置到它所在的块的右端点之间的逆序对数(用树状数组做$O(nlogn)$).
$ans[i][j]$___表示第$i$块到第$j$块之间的逆序对数(时间复杂度为块数乘块数再乘以每次枚举每个块, 三个$sqrt(n)$, 即为$O(n*sqrt(n))$).
$cnt[i][j]$___表示第$i$块及以前中大于$j$的个数(可以先处理这个, 再处理$ans$数组, 因为有了这个后$ans$会好推很多). 该数组可以先将第$i$块中的每个数字打上$1$, 再做一遍后缀和, 一遍前缀和(具体看代码)($O(n*sqrt(n))$).

询问时:

如果在同一块内, 那么答案就是$pre[r] - pre[l - 1]$ 再减去左端点到块的左端点之间与右端点到左端点之间的贡献.
否则答案就是$suf[l] + pre[r] + $整块间的贡献($ans$数组所记录的答案)$+$左右两个散块之间的贡献$+$左右两个散块分别与整块之间的答案.

对于左右两个散块分别与整块之间的答案, 我们用预处理的$cnt$数组就行了. 而对于左右两个散块之间的贡献我们可以事先另开一个数组为块内排好序后的结果, 查询时用归并排序的方法求逆序对数, 是$O(sqrt(n))$(块长)的.

小提示: 块长设计成$sqrt(n)/2$会更优, 且千万不要写$define$ $int$ $long$ $long$这种东西.

#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define Maxn 100000
#define Maxs 1000
using namespace std;
int read() {
	int f = 1, sum = 0;
	char ch = getchar();
	while(ch < '0' || ch > '9') {
		if(ch == '-') f = -1;
		ch = getchar();
	}
	while(ch >= '0' && ch <= '9') {
		sum = sum * 10 + ch - '0';
		ch = getchar();
	}
	return f * sum;
}
void write(long long x) {
	(x < 0) ? (putchar('-'), write(-x)) : (void)((x <= 9) ? (putchar(x + '0')) : (write(x / 10), putchar(x % 10 + '0')));
}
int n, a[Maxn + 9], in[Maxn + 9], c[Maxs + 9][Maxn + 9], mg1[Maxn + 9], mg2[Maxn + 9], m1, m2, pre[Maxn + 9], suf[Maxn + 9];
long long ans, f[Maxs + 9][Maxs + 9]/*即ans数组*/;
struct BLOCK {
	int l, r;
} b[Maxs + 9];
struct SORTED {
	int num, id;
} sorted[Maxn + 9];
bool CmpNum(SORTED x, SORTED y) {
	return x.num < y.num;
}
int tree[Maxn + 9];
int LowBit(int x) {
	return x & -x;
}
void Update(int x, int y) {
	for(; x <= n; x += LowBit(x)) {
		tree[x] += y;
	}
}
int Query(int x) {
	int asdfg = 0;
	for(; x; x -= LowBit(x)) {
		asdfg += tree[x];
	}
	return asdfg;
}
int min(int x, int y) {
	return x < y ? x : y;
}
signed main() {
	n = read();
	int T = read();
	int Base = sqrt(n) / 2.1, S = ceil(1.0 * n / Base);
	for(int i = 1; i <= n; ++i) {
		sorted[i].num = a[i] = read();
		sorted[i].id = i;
		in[i] = (i - 1) / Base + 1;
	}
	for(int i = 1; i <= S; ++i) {
		b[i].l = (i - 1) * Base + 1, b[i].r = min(n, i * Base);
		sort(sorted + b[i].l, sorted + b[i].r + 1, CmpNum);
		memset(tree, 0, sizeof(tree));
		Update(a[b[i].l], 1);
		for(int j = b[i].l + 1; j <= b[i].r; ++j) {
			pre[j] = Query(n) - Query(a[j]) + pre[j - 1];
			Update(a[j], 1);
		}
		memset(tree, 0, sizeof(tree));
		Update(a[b[i].r], 1);
		for(int j = b[i].r - 1; j >= b[i].l; --j) {
			suf[j] = Query(a[j]) + suf[j + 1];
			Update(a[j], 1);
		}
		f[i][i] = pre[b[i].r];
	}
	for(int i = 1; i <= S; ++i) {
		for(int j = b[i].l; j <= b[i].r; ++j) {
			++c[i][a[j]];
		}
	}
	for(int i = 1; i <= S; ++i) {
		for(int j = n - 1; j >= 1; --j) {
			c[i][j] += c[i][j + 1];
		}
	}
	for(int i = 1; i <= S; ++i) {
		for(int j = 1; j <= n; ++j) {
			c[i][j] += c[i - 1][j];
		}
	}
	for(int i = 1; i <= S; ++i) {
		for(int j = i + 1; j <= S; ++j) {
			f[i][j] = f[i][j - 1] + f[j][j];
			for(int k = b[j].l; k <= b[j].r; ++k) {
				f[i][j] += c[j - 1][a[k]] - c[i - 1][a[k]];
			}
		}
	}
	while(T--) {
		int l = read()^ans, r = read()^ans;
		if(l >= r) {
			ans = 0;
			write(ans);
			putchar('\n');
			continue;
		}
		if(in[l] == in[r]) {
			ans = pre[r];
			if(l > b[in[l]].l) ans -= pre[l - 1];
			m1 = m2 = 0;
			for(int i = b[in[l]].l; i <= b[in[l]].r; ++i) {
				if(sorted[i].id < l) mg1[++m1] = sorted[i].num;
				if(sorted[i].id >= l && sorted[i].id <= r) mg2[++m2] = sorted[i].num;
			}
			int p1 = 1, p2 = 1;
			while(p1 <= m1 && p2 <= m2) {
				if(mg1[p1] > mg2[p2]) ans -= m1 - p1 + 1, ++p2;
				else ++p1;
			}
			write(ans);
			putchar('\n');
			continue;
		}
		ans = suf[l] + pre[r];
		m1 = m2 = 0;
		for(int i = b[in[l]].l; i <= b[in[l]].r; ++i) if(sorted[i].id >= l) mg1[++m1] = sorted[i].num;
		for(int i = b[in[r]].l; i <= b[in[r]].r; ++i) if(sorted[i].id <= r) mg2[++m2] = sorted[i].num;
		int p1 = 1, p2 = 1;
		while(p1 <= m1 && p2 <= m2) {
			if(mg1[p1] > mg2[p2]) ans += m1 - p1 + 1, ++p2;
			else ++p1;
		}
		if(in[l] + 1 == in[r]) {
			write(ans);
			putchar('\n');
			continue;
		}
		ans += f[in[l] + 1][in[r] - 1];
		for(int i = l; i <= b[in[l]].r; ++i) ans += b[in[r] - 1].r - b[in[l] + 1].l + 1 - (c[in[r] - 1][a[i]] - c[in[l]][a[i]]);
		for(int i = b[in[r]].l; i <= r; ++i) ans += c[in[r] - 1][a[i]] - c[in[l]][a[i]];
		write(ans);
		putchar('\n');
		continue;
	}
	return 0;
}

完结不撒花~

posted @ 2022-07-22 14:15 TuSalcc 阅读(96) 评论(0) 收藏举报

刷新页面返回顶部

TuSalcc

Welcome to TuSalcc's blog!

分块