线段树

线段树的分类有很多但感觉写来写去原理都差不多，学一点写一点，持续更新

希望大佬们能 (指出错误)||(提出意见)

序号	类型
1	普通线段树
2	值域线段树
3	线段树的分裂与合并
4	可持久化线段树(主席树)

普通线段树

思想

普通线段树是一种用以维护区间信息的数据结构，方法是在原序列上建一棵二叉树。

普通线段树中每个叶子结点的信息为它所对应的序列中的元素的信息，非叶子结点记录的是以该节点为根的子树的信息，实现时将左儿子和右儿子的信息整合即可。

那么，为什么我们要用线段树来维护信息呢？举个例子：

给你一个长为 $n$ 序列 $a[1], a[2]...a[n-1],a[n]$ , 并且有 $m$ 个操作，分为两种: 1. 将某个位置的值加上一个数; 2. 查询某个区间的和。强制在线。

没学过数据结构的话当然先考虑暴力，修改时直接在数组上修改，查询时将区间内的元素暴力扫一遍就好了。但是如果 $n,m$ 都是 $10^5$ 的范围，且每次操作都询问 $1-n$ 的和，那肯定 $T$ 飞了。
所以有了线段树，如图：

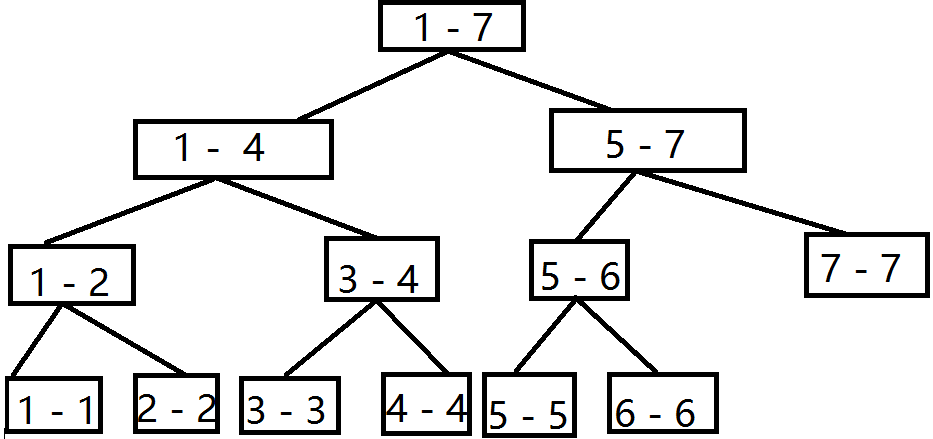
众所周知，在叶子结点为 $n$ 的二叉树中，总结点数约为 $2n$, 深度最大为 $logn$, 所以修改为 $O(logn)$, 查询也为 $O(logn)$, 因为当我们跑到的节点所维护的区间在查询区间中时，可以直接将该节点的信息返回。

那么区间修改呢？暴力很容易想到一个点一个点去改，但这样的话我们的速度反而比朴素的暴力更慢了。这时，我们想到了懒标记 ( $lazy$ ).假如我们跑到的节点所维护的区间在修改区间中时，在该节点上打上懒标记，下一次若需要遍历到该节点的子节点时，将懒标记打掉推给两个儿子。回溯时再用两个儿子的信息来维护该节点的信息即可。

模板 (洛谷 P3372【模板】线段树 1)

#include<cstdio>
#define int long long 
#define MAXN 200000
using namespace std;
struct Svv {
    int val, lazy, l, r;
} c[(MAXN << 2) + 9];		//开四倍大小
int n, m, a[MAXN + 9];
int read() {
    int f = 1, sum = 0;
    char ch = getchar();
    while(ch < '0' || ch > '9') {
        if(ch == '-') f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9') {
        sum = sum * 10 + ch - '0';
        ch = getchar();
    }
    return f * sum;
}
void write(long long x) {
	(x < 0) ? (putchar('-'), write(-x)) : (void)((x <= 9) ? (putchar(x + '0')) : (write(x / 10), putchar(x % 10 + '0')));
}
void PushUp(int k) {		//从两个儿子那儿更新信息
    c[k].val = c[k << 1].val + c[k << 1 | 1].val;
}
void PushDown(int k) {		//将懒标记向下推向两个儿子
    if(c[k].lazy) {
        c[k << 1].lazy += c[k].lazy;
        c[k << 1 | 1].lazy += c[k].lazy;
        c[k << 1].val += c[k].lazy * (c[k << 1].r - c[k << 1].l + 1);
        c[k << 1 | 1].val += c[k].lazy * (c[k << 1 | 1].r - c[k << 1 | 1].l + 1);
        c[k].lazy = 0;	//打掉懒标记
    }
}
void Build(int k, int l, int r) {		//建树
    c[k].l = l;
    c[k].r = r;
    if(l == r) {
        c[k].val = a[l];
        return;
    }
    int mid = l + r >> 1;
    Build(k << 1, l, mid);
    Build(k << 1 | 1, mid + 1, r);
    PushUp(k);
}
void Update(int k, int l, int r, int p) {		//更新
    if(c[k].l >= l && c[k].r <= r) {
        c[k].lazy += p;
        c[k].val += p * (c[k].r - c[k].l + 1);
        return;
    }
    PushDown(k);
    int mid = c[k].l + c[k].r >> 1;
    if(l <= mid) Update(k << 1, l, r, p);
    if(mid + 1 <= r) Update(k << 1 | 1, l, r, p);
    PushUp(k);
}
int Query(int k, int l, int r) {		//查询
    if(c[k].l >= l && c[k].r <= r) {
        return c[k].val;
    }
    PushDown(k);
    int ans = 0, mid = c[k].l + c[k].r >> 1;
    if(l <= mid) ans += Query(k << 1, l, r);
    if(mid + 1 <= r) ans += Query(k << 1 | 1, l, r);
    return ans;
}
signed main() {
    n = read(), m = read();
    for(int i = 1; i <= n; ++i) {
        a[i] = read();
    }
    Build(1, 1, n);
    for(int i = 1; i <= m; ++i) {
        int op = read();
        if(op == 1) {
            int l = read(), r = read(), p = read();
            Update(1, l, r, p);
        }
        else {
            int l = read(), r = read();
            write(Query(1, l, r));
            putchar('\n');
        }
    }
    return 0;
}

维护其他信息时，本质是相同的。而且还可以同时维护多种信息，如同时维护最小值和区间 $gcd$.
线段树可用来验证答案或优化 dp 之类的

例题 (洛谷 P2824 [HEOI2016/TJOI2016] 排序)

先膜拜一下fy0123(无晴) 大佬.能想到这种简洁明了的方法真是 TQL%%%.

首先二分答案，再去验证这个答案是否正确。具体方法就是先二分 ($1$ ~ $n$),并将原序列中大于等于$mid$的值标为$1$, 其余标为$0$.然后将得到的$01$序按给的操作排序 (查询这段区间内的为$sum$,即$1$的个数。若为升序排序就将改区间后$sum$个位置更新为$1$,前$l - r + 1 - sum$位更新为$0$.降序同理).若排完序后第$q$个元素为$1$,说明答案还可以更大或就是$mid$, 所以记下$mid$并将左端点右移，否则右端点左移。

#include<cstdio>
#define int long long
#define Maxn 100000
using namespace std;
int read() {
	int f = 1, sum = 0;
	char ch = getchar();
	while(ch < '0' || ch > '9') {
		if(ch == '-') f = -1;
		ch = getchar();
	}
	while(ch >= '0' && ch <= '9') {
		sum = sum * 10 + ch - '0';
		ch = getchar();
	}
	return f * sum;
}
void write(int x) {
	(x < 0) ? (putchar('-'), write(-x)) : (void)((x <= 9) ? (putchar(x + '0')) : (write(x / 10), putchar(x % 10 + '0')));
}
int n, m, q, a[Maxn + 9], b[Maxn + 9];
struct CZ {
	int opt, l, r;
} cz[Maxn + 9];
struct XDS {
	int val, lazy, l, r;
} c[(Maxn << 2) + 9];
void PushUp(int p) {
	c[p].val = c[p << 1].val + c[p << 1 | 1].val;
}
void PushDown(int p) {
	if(c[p].lazy == -1) {
		c[p << 1].val = 0, c[p << 1].lazy = -1, c[p << 1 | 1].val = 0, c[p << 1 | 1].lazy = -1;
	}
	if(c[p].lazy == 1) {
		c[p << 1].val = c[p << 1].r - c[p << 1].l + 1, c[p << 1].lazy = 1, c[p << 1 | 1].val = c[p << 1 | 1].r - c[p << 1 | 1].l + 1, c[p << 1 | 1].lazy = 1;
	}
	c[p].lazy = 0;
}
void Build(int p, int l, int r) {
	c[p].l = l, c[p].r = r, c[p].lazy = 0, c[p].val = 0;
	if(l == r) {
		c[p].val = b[l];
		return;
	}
	int mid = l + r >> 1;
	Build(p << 1, l, mid);
	Build(p << 1 | 1, mid + 1, r);
	PushUp(p);
}
void Update(int p, int l, int r, int L, int R, int val) {
	if(L > R) return;
	if(l >= L && r <= R) {
		if(val == -1) {
			c[p].val = 0, c[p].lazy = -1;
		} else {
			c[p].val = r - l + 1, c[p].lazy = 1;
		}
		return;
	}
	PushDown(p);
	int mid = l + r >> 1;
	if(L <= mid) Update(p << 1, l, mid, L, R, val);
	if(mid + 1 <= R) Update(p << 1 | 1, mid + 1, r, L, R, val);
	PushUp(p);
}
int Query(int p, int l, int r, int L, int R) {
	if(l >= L && r <= R) {
		return c[p].val;
	}
	PushDown(p);
	int mid = l + r >> 1, ans = 0;
	if(L <= mid) ans += Query(p << 1, l, mid, L, R);
	if(mid + 1 <= R) ans += Query(p << 1 | 1, mid + 1, r, L, R);
	return ans;
}
void Solve(int mid) {
	for(int i = 1; i <= n; ++i) {
		if(a[i] >= mid) b[i] = 1;
		else b[i] = 0;
	}
	Build(1, 1, n);
	for(int i = 1; i <= m; ++i) {
		int sum = Query(1, 1, n, cz[i].l, cz[i].r);
		if(sum == cz[i].r - cz[i].l + 1 || sum == 0) continue;
		if(cz[i].opt == 0) {
			Update(1, 1, n, cz[i].r - sum + 1, cz[i].r, 1);
			Update(1, 1, n, cz[i].l, cz[i].r - sum, -1);
		} else {
			Update(1, 1, n, cz[i].l, cz[i].l + sum - 1, 1);
			Update(1, 1, n, cz[i].l + sum, cz[i].r, -1);
		}
	}
}
signed main() {
	n = read(), m = read();
	for(int i = 1; i <= n; ++i) a[i] = read();
	for(int i = 1; i <= m; ++i) {
		cz[i].opt = read(), cz[i].l = read(), cz[i].r = read();
	}
	q = read();
	int left = 1, right = n, mid, ans;
	while(left <= right) {
		mid = left + right >> 1;
		Solve(mid);
		if(Query(1, 1, n, q, q)) left = mid + 1;
		else right = mid - 1;
	}
	Solve(left);
	if(Query(1, 1, n, q, q)) write(left);
	else write(right);
	return 0;
}

值域线段树

~~我比较喜欢叫权值线段树 (叫法什么的不重要)~~

顾名思义，值域线段树就是将原序列的值作为一个新的序列来构建一个线段树。比如有一个集合 $S$ , 每一个元素的范围是 $1 - 10^5$, 那么我们就可以建造一棵维护数字出现次数的线段树，可以查询某个范围内的数字在这个集合中出现了几次，支持删除和插入，和普通线段树的更新操作一样。
例题就不放了，主要运用方法和树状数组差不多，但主席树 (下面讲到) 不能用树状数组。

线段树的分裂与合并

线段树分裂

我们要将原序列分成两段来维护，分割点为$x$,则将原线段树分裂成两个，前一个维护$1$ ~ $x$ 的信息，后一个维护 $ x + 1 $ ~ $ n $ 的信息。

附：动态开点

但是有没有想到，分个几次之后空间会爆的很惨。所以我们可以动态开点.在值域线段树中，有一些数字在原集合中没有出现，但是我们还是给它开了空间 (这是完全不需要的),所以我们就可以选择只有当这个数字出现后才去开这条路上的点。这样的话我们每个节点维护的信息还要加上它左儿子的编号和右儿子的编号。

开点过程

不用建树，枚举元素一个个更新就好了。直接建树的话空间就和普通线段树没什么区别了

void UpDate(int &p, int l, int r, int x, int y) {
	if(!p) {
		p = ++cnt;				//新建结点
	}
	t[p].val += y;				//单点更新可以直接在路径上加，因为它所到的节点所维护的区间必定是包含它的，稍微想想就知道
	if(l == r) {
		return;
	}
	int mid = l + r >> 1;
	if(l <= x && x <= mid) UpDate(t[p].ls, l, mid, x, y);
	if(mid + 1 <= x && x <= r) UpDate(t[p].rs, mid + 1, r, x, y);
//	PushUp(p); 否则还要像普通线段树那样在叶子结点加再 PushUp
}

线段树分裂代码

void Split(int p, int &q, int x) {		//p是原结点,分裂出去的结点放在q中,剩下的仍在p中,即分裂成了结点p和结点q
	if(!p) return;
	q = input();
	if(t[t[p].ls].val < x) {
		Split(t[p].rs, t[q].rs, x - t[t[p].ls].val);
	}
	else {
		Swap(t[p].rs, t[q].rs);
	}
	if(t[t[p].ls].val > x) {
		Split(t[p].ls, t[q].ls, x);
	}
	t[q].val = t[p].val - x;
	t[p].val = x;
}

线段树合并

线段树合并就是将两个线段树维护相同区间的结点合并成为一个.注意我们是把第二个结点中的信息放入第一个结点,但第二个结点并未消失.为了节约空间,我们可以"回收"这些结点,放入一个"仓库"中,下次开点时可以使用.

线段树合并代码

void Merge(int &p, int q) {
	if(!p) {
		Swap(p, q);
		return;
	}
	t[p].val += t[q].val;
	if(t[q].ls) Merge(t[p].ls, t[q].ls);
	if(t[q].rs) Merge(t[p].rs, t[q].rs);
}

回收节点

int input() {			//新建结点p = input()
	if(tail) {
		int t = stack[tail];
		--tail;
		return t;
	}
	return ++cnt;
}
void del(int p) {		//删除结点并放入回收"栈"del(p)
	stack[++tail] = p;
	t[p].val = t[p].rs = t[p].ls = 0;
	return ;
}

模板(洛谷 P5494 【模板】线段树分裂)

#include<cstdio>
#define int long long
#define Maxn 200000
using namespace std;
int read() {
	int f = 1, sum = 0;
	char ch = getchar();
	while(ch < '0' || ch > '9') {
		if(ch == '-') f = -1;
		ch = getchar();
	}
	while(ch >= '0' && ch <= '9') {
		sum = sum * 10 + ch - '0';
		ch = getchar();
	}
	return f * sum;
}
void write(int x) {
    (x < 0) ? (putchar('-'), write(-x)) : (void)((x <= 9) ? (putchar(x + '0')) : (write(x / 10), putchar(x % 10 + '0')));
}
int n, T, cnt, roots = 1, root[Maxn + 9], stack[(Maxn << 5) + 9], tail;
struct Svv {
	int val, ls, rs;
} t[(Maxn << 5) + 9];
void Swap(int &a, int &b) {
	int t = a;
	a = b;
	b = t;
}
int input() {
	if(tail) {
		int t = stack[tail];
		--tail;
		return t;
	}
	return ++cnt;
}
void del(int p) {
	stack[++tail] = p;
	t[p].val = t[p].rs = t[p].ls = 0;
	return ;
}
void UpDate(int &p, int l, int r, int x, int y) {
	if(!p) {
		p = input();
	}
	t[p].val += y;
	if(l == r) {
		return;
	}
	int mid = l + r >> 1;
	if(l <= x && x <= mid) UpDate(t[p].ls, l, mid, x, y);
	if(mid + 1 <= x && x <= r) UpDate(t[p].rs, mid + 1, r, x, y);
}
void Split(int p, int &q, int x) {
	if(!p) return;
	q = input();
	if(t[t[p].ls].val < x) {
		Split(t[p].rs, t[q].rs, x - t[t[p].ls].val);
	}
	else {
		Swap(t[p].rs, t[q].rs);
	}
	if(t[t[p].ls].val > x) {
		Split(t[p].ls, t[q].ls, x);
	}
	t[q].val = t[p].val - x;
	t[p].val = x;
}
void Merge(int &p, int q) {
	if(!p) {
		Swap(p, q);
		return;
	}
	t[p].val += t[q].val;
	if(t[q].ls) Merge(t[p].ls, t[q].ls);
	if(t[q].rs) Merge(t[p].rs, t[q].rs);
	del(q);
}
int QuerySum(int p, int l, int r, int L, int R) {
	if(!p) return 0;
	if(L >= l && R <= r) {
		return t[p].val;
	}
	int mid = L + R >> 1, ans = 0;
	if(l <= mid) {
		ans += QuerySum(t[p].ls, l, r, L, mid);
	}
	if(mid + 1 <= r) {
		ans += QuerySum(t[p].rs, l, r, mid + 1, R);
	}
	return ans;
}
int QueryNum(int p, int k, int L, int R) {
	if(L == R) {
		return L;
	}
	int mid = L + R >> 1;
	if(t[t[p].ls].val >= k) return QueryNum(t[p].ls, k, L, mid);
	if(t[t[p].ls].val < k) return QueryNum(t[p].rs, k - t[t[p].ls].val, mid + 1, R);
}
void Solve() {
	int opt = read();
	if(opt == 0) {
		int p = read(), x = read(), y = read();
		int t1 = QuerySum(root[p], 1, x - 1, 1, n);
		int t2 = QuerySum(root[p], x, y, 1, n);
		Split(root[p], root[++roots], t1);
		int ttt = 0;
		Split(root[roots], ttt, t2);
		Merge(root[p], ttt);
	}
	else if(opt == 1) {
		int p = read(), t = read();
		Merge(root[p], root[t]);
	}
	else if(opt == 2) {
		int p = read(), x = read(), q = read();
		UpDate(root[p], 1, n, q, x);
	}
	else if(opt == 3) {
		int p = read(), x = read(), y = read();
		write(QuerySum(root[p], x, y, 1, n));
		putchar('\n');
	}
	else {
		int p = read(), k = read();
		if(t[root[p]].val < k) {
			write(-1);
			putchar('\n');
			return;
		}
		write(QueryNum(root[p], k, 1, n));
		putchar('\n');
	}
}
signed main() {
	n = read(), T = read();
	for(int i = 1; i <= n; ++i) {
		int temp = read();
		UpDate(root[roots], 1, n, i, temp);
	}
	while(T--) {
		Solve();
	}
	return 0;
}

例题(洛谷 P3521 [POI2011]ROT-Tree Rotations)

由于一个结点的左右两个子树无论怎样变换,子树间的元素的相对大小是不会改变的.而当两个子树都是叶子结点时,我们一定能做到两个叶子结点间不产生贡献.所以我们只要递归回溯时合并两个子树带来的贡献即可.定义两个变量,一个是交换带来的最小贡献,一个是不交换带来的最小贡献.

#include<cstdio>
#define int long long
#define Maxn 200000
using namespace std;
int read() {
    int f = 1, sum = 0;
    char ch = getchar();
    while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
    while(ch >= '0' && ch <= '9') sum = sum * 10 + ch - '0', ch = getchar();
    return sum * f;
}
void write(int x) {
    (x < 0) ? (putchar('-'), write(-x)) : (void)((x <= 9) ? (putchar(x + '0')) : (write(x / 10), putchar(x % 10 + '0')));
}
struct Svv {
	int val, l, r;
} t[(Maxn << 5) + 9];
int n, change, nochange, cnt, ans;
int min(int x, int y) {
	return x < y ? x : y; 
}
int UpDate(int l, int r, int val) {
	int root = ++cnt;
	++t[root].val;
	if(l == r) return root;
	int mid = l + r >> 1;
	if(val <= mid) t[root].l = UpDate(l, mid, val);
	if(val >= mid + 1) t[root].r = UpDate(mid + 1, r, val);
	return root;
}
int merge(int x, int y, int l, int r) {
	if(!x) return y;
	if(!y) return x;
	if(l == r) {
		t[x].val += t[y].val;
		return x;
	}
	nochange += t[t[x].r].val * t[t[y].l].val;
	change += t[t[y].
	r].val * t[t[x].l].val;
	int mid = l + r >> 1;
	t[x].l = merge(t[x].l, t[y].l, l, mid);
	t[x].r = merge(t[x].r, t[y].r, mid + 1, r);
	t[x].val += t[y].val;
	return x;
}
int dfs() {
	int val = read(), root;
	if(val == 0) {
		int left = dfs(), right = dfs();
		change = 0;
		nochange = 0;
		root = merge(left, right, 1, n);
		ans += min(change, nochange);
	}
	else {
		root = UpDate(1, n, val);
	}
	return root;
}
signed main() {
	n = read();
	int root = dfs();
	write(ans);
	return 0;
}

可持久化线段树

这个要从例题讲起

洛谷 P3919 【模板】可持久化线段树 1（可持久化数组）

题目背景

UPDATE : 最后一个点时间空间已经放大

2021.9.18 增添一组 hack 数据 by @panyf

标题即题意

有了可持久化数组，便可以实现很多衍生的可持久化功能（例如：可持久化并查集）

题目描述

如题，你需要维护这样的一个长度为 $ N $ 的数组，支持如下几种操作

在某个历史版本上修改某一个位置上的值
访问某个历史版本上的某一位置的值

此外，每进行一次操作（对于操作2，即为生成一个完全一样的版本，不作任何改动），就会生成一个新的版本。版本编号即为当前操作的编号（从1开始编号，版本0表示初始状态数组）

输入格式

输入的第一行包含两个正整数 $ N, M $，分别表示数组的长度和操作的个数。

第二行包含$ N $个整数，依次为初始状态下数组各位的值（依次为 $ a_i $，$ 1 \leq i \leq N $）。

接下来$ M $行每行包含3或4个整数，代表两种操作之一（$ i $为基于的历史版本号）：

对于操作1，格式为$ v_i \ 1 \ {loc}_i \ {value}i $，即为在版本$ v_i $的基础上，将 $ a_i} $ 修改为 $ {value}_i $
对于操作2，格式为$ v_i \ 2 \ {loc}i $，即访问版本$ v_i $中的 $ a_i} $的值，生成一样版本的对象应为vi

输出格式

输出包含若干行，依次为每个操作2的结果。

样例 #1

样例输入 #1

5 10
59 46 14 87 41
0 2 1
0 1 1 14
0 1 1 57
0 1 1 88
4 2 4
0 2 5
0 2 4
4 2 1
2 2 2
1 1 5 91

样例输出 #1

提示

数据规模：

对于30%的数据：$ 1 \leq N, M \leq {10}^3 $

对于50%的数据：$ 1 \leq N, M \leq {10}^4 $

对于70%的数据：$ 1 \leq N, M \leq {10}^5 $

对于100%的数据：$ 1 \leq N, M \leq {10}^6, 1 \leq {loc}_i \leq N, 0 \leq v_i < i, -{10}^9 \leq a_i, {value}_i \leq {10}^9$

经测试，正常常数的可持久化数组可以通过，请各位放心

~~数据略微凶残，请注意常数不要过大~~

~~另，此题I/O量较大，如果实在TLE请注意I/O优化~~

询问生成的版本是指你访问的那个版本的复制

样例说明：

一共11个版本，编号从0-10，依次为：

* 0 : 59 46 14 87 41

* 1 : 59 46 14 87 41

* 2 : 14 46 14 87 41

* 3 : 57 46 14 87 41

* 4 : 88 46 14 87 41

* 5 : 88 46 14 87 41

* 6 : 59 46 14 87 41

* 7 : 59 46 14 87 41

* 8 : 88 46 14 87 41

* 9 : 14 46 14 87 41

* 10 : 59 46 14 87 91

首先我们很容易想到在每个时间都建一棵线段树,但这样时间空间双爆...
经过我们~~仔细认真绞尽脑汁地~~思考,发现当我们更改一个位置时,只有一条路上的信息会发生改变(如图),而其他的信息完全可以直接引用原结点,所以我们只要新建一条链就好了,不需要再建一棵树.如果是更改操作直接引用上一个版本的根节点就好了.

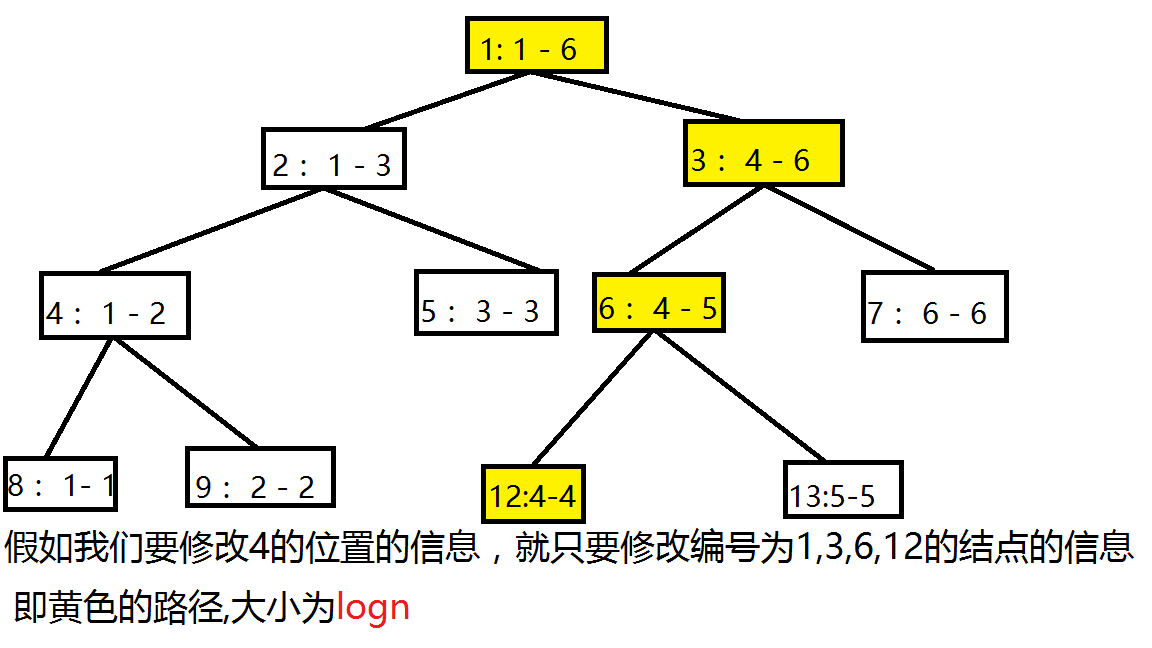
所以我们就可以这么新建版本(蓝色的链为新建的链):

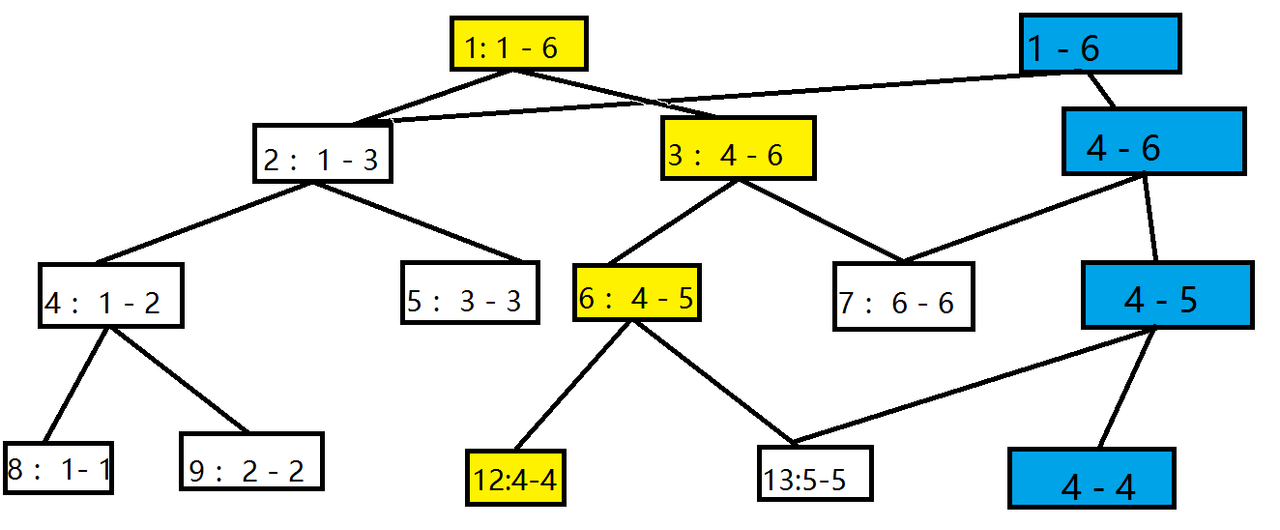
代码

#include<cstdio>
#define Maxn 1000000
using namespace std;
int read() {
	int f = 1, sum = 0;
	char ch = getchar();
	while(ch < '0' || ch > '9') {
		if(ch == '-') f = -1;
		ch = getchar();
	}
	while(ch >= '0' && ch <= '9') {
		sum = sum * 10 + ch - '0';
		ch = getchar();
	}
	return sum * f;
}
void write(int x) {
	(x < 0) ? (putchar('-'), write(0 - x)) : (void)((x <= 9) ? (putchar(x + '0')) : (write(x / 10), putchar(x % 10 + '0')));
} 
struct Svv {
	int val, l, r, L, R;
} t[(Maxn << 6) + 9];
int a[Maxn + 9], root[Maxn + 9], cnt;
void Build(int &newt, int L, int R) {
	newt = ++cnt;
	t[newt].L = L, t[newt].R = R;
	if(L >= R) {
		t[newt].val = a[L];
		return;
	}
	int mid = L + R >> 1;
	Build(t[newt].l, L, mid);
	Build(t[newt].r, mid + 1, R);
}
void UpDate(int &newt, int oldt, int loc, int val) {
	newt = ++cnt;
	t[newt] = t[oldt];
	if(t[newt].L == t[newt].R) {
		t[newt].val = val;
		return;
	}
	int mid = t[newt].L + t[newt].R >> 1;
	if(loc <= mid) {
		UpDate(t[newt].l, t[oldt].l, loc, val);
	}
	if(loc > mid) {
		UpDate(t[newt].r, t[oldt].r, loc, val);
	}
}
int Query(int p, int loc) {
	if(t[p].L == t[p].R && t[p].L == loc) {
		return t[p].val;
	}
	int mid = t[p].L + t[p].R >> 1;
	if(loc <= mid) return Query(t[p].l, loc);
	if(loc > mid) return Query(t[p].r, loc);
}
void run(int i) {
	int v = read(), opt = read(), loc = read();
	if(opt == 1) {
		int val = read();
		UpDate(root[i], root[v], loc, val);
	}
	else {
		root[i] = root[v];
		write(Query(root[i], loc));
		putchar('\n');
	}
}
signed main() {
	int n = read(), m = read();
	for(int i = 1; i <= n; ++i) {
		a[i] = read();
	}
	Build(root[0], 1, n);
	for(int i = 1; i <= m; ++i) {
		run(i);
	}
	return 0;
}

第二个模板(主席树运用)(洛谷 P3834 【模板】可持久化线段树 2)

时间可以当做一个新的维度,这样从左往右扫序列时每多一个元素就可以再建一个版本的值域线段树,查询时同一结点右边的版本的信息与左边版本信息的差即为该区间的信息.一个值域线段树可以解决序列第 $k$ 大,上述方法即可解决区间第 $k$ 大.

#include<cstdio>
#include<algorithm>
#define Maxn 200000
using namespace std;
int Read() {
	int f = 1, sum = 0;
	char ch = getchar();
	while(ch < '0' || ch > '9') {
		if(ch == '-') f = -1;
		ch = getchar();
	}
	while(ch >= '0' && ch <= '9') {
		sum = sum * 10 + ch - '0';
		ch = getchar();
	}
	return sum * f;
}
int n, m, hash[Maxn + 9], root[Maxn + 9], sum, num;
struct SZ {
	int num, id;
} a[Maxn + 9];
struct ZXS {
	int val, L, R;
} t[Maxn * 20 + 9];
bool CmpNum(SZ x, SZ y) {
	return x.num < y.num;
}
bool CmpId(SZ x, SZ y) {
	return x.id < y.id;
}
void Hash() {
	sort(a + 1, a + n + 1, CmpNum);
	sum = 0;
	int last;
	for(int i = 1; i <= n; ++i) {
		if(i == 1 || a[i].num != last) {
			last = a[i].num;
			hash[++sum] = a[i].num;
		}
		a[i].num = sum;
	}
	sort(a + 1, a + n + 1, CmpId);
}
void UpDate(int &newt, int oldt, int l, int r, int k) {
	newt = ++num;
	t[newt] = t[oldt];
	++t[newt].val;
	if(l == r) return;
	int mid = l + r >> 1;
	if(k <= mid) UpDate(t[newt].L, t[oldt].L, l, mid, k);
	else UpDate(t[newt].R, t[oldt].R, mid + 1, r, k);
}
int Query(int i, int j, int l, int r, int k) {
	if(l == r) return l;
	int mid = l + r >> 1, val = t[t[j].L].val - t[t[i].L].val;
	if(k <= val) return Query(t[i].L, t[j].L, l, mid, k);
	else return Query(t[i].R, t[j].R, mid + 1, r, k - val);
}
signed main() {
	n = Read(), m = Read();
	for(int i = 1; i <= n; ++i) {
		a[i].num = Read();
		a[i].id = i;
	}
	Hash();
	for(int i = 1; i <= n; ++i) {
		UpDate(root[i], root[i - 1], 1, sum, a[i].num);
	}
	while(m--) {
		int L = Read(), R = Read(), k = Read();
		printf("%d\n", hash[Query(root[L - 1], root[R], 1, sum, k)]);
	}
	return 0;
}

例题1(洛谷 P3567 [POI2014]KUR-Couriers)

像前一题一样的方法,我们可以维护区间信息.假设我们遍历到了一个结点,左儿子的信息(两个版本的差)若超过一半,就向左跑.若右儿子的信息(两个版本的差)超过一半,就往右边跑.若最后成功跑到了叶子结点,说明该叶子结点代表的数即为所求值.反之,则说明没有.

#include<cstdio>
#include<algorithm>
#define Maxn 500000
using namespace std;
int read() {
    int f = 1, sum = 0;
    char ch = getchar();
    while(ch < '0' || ch > '9') {
        if(ch == '-') f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9') {
        sum = sum * 10 + ch - '0';
        ch = getchar();
    }
    return sum * f;
}
void write(int x) {
    (x < 0) ? (putchar('-'), write(0 - x)) : (void)((x <= 9) ? (putchar(x + '0')) : (write(x / 10), putchar(x % 10 + '0')));
} 
struct Svv {
    int val, l, r;
} t[(Maxn << 5) + 9];
struct Emm {
    int num, id;
} a[Maxn + 9];
int n, m, hash[Maxn + 9], cnt, Max, root[Maxn + 9];
bool CmpNum(Emm x, Emm y) {
    return x.num < y.num;
}
bool CmpId(Emm x, Emm y) {
    return x.id < y.id;
}
void Hash() {
    sort(a + 1, a + n + 1, CmpNum);
    int last, sum = 0;
    for(int i = 1; i <= n; ++i) {
        if(i == 1 || a[i].num != last) {
            last = a[i].num;
            hash[++sum] = a[i].num;
        }
        a[i].num = sum;
    }
    Max = sum;
    sort(a + 1, a + n + 1, CmpId);
}
void UpDate(int &newt, int oldt, int L, int R, int val) {
    newt = ++cnt;
    t[newt] = t[oldt];
    ++t[newt].val;
    if(L == R) return;
    int mid = L + R >> 1;
    if(val <= mid) UpDate(t[newt].l, t[oldt].l, L, mid, val);
    if(val > mid) UpDate(t[newt].r, t[oldt].r, mid + 1, R, val);
}
int Query(int p, int q, int L, int R, int k) {
    if(L == R) return L;
    int mid = L + R >> 1, t1 = t[t[q].l].val - t[t[p].l].val, t2 = t[t[q].r].val - t[t[p].r].val;
    if(t1 > k) return Query(t[p].l, t[q].l, L, mid, k);
    else if(t2 > k) return Query(t[p].r, t[q].r, mid + 1, R, k);
    else return 0;
}
void solve() {
    int l = read(), r = read();
    write(hash[Query(root[l - 1], root[r], 1, Max, (r - l + 1) >> 1)]);
    putchar('\n');
}
signed main() {
    n = read(), m = read();
    for(int i = 1; i <= n; ++i) {
        a[i].num = read();
        a[i].id = i;
    }
    Hash();
    for(int i = 1; i <= n; ++i) {
        UpDate(root[i], root[i - 1], 1, Max, a[i].num);
    }
    for(int i = 1; i <= m; ++i) {
        solve();
    }
    return 0;
}

例题2(洛谷 P2048 [NOI2010] 超级钢琴)

题意: 在一段长度为 $n$ 的序列中,选取 $k$ 段不同连续序列,且每段序列的长度在 $L$ ~ $R$ 之间,使得这 $k$ 段序列的和最大.

所以我们可以记录以 $i$ 为右端点时最大的和,这个值可以先做一遍前缀和,再选 $max(1, i - R + 1)$ ~ $i - L + 1$ 之间最小的 $sum$ 值.为了每次都取最大的,我们可以把每个值都丢到一个大根堆中,每次取最大的.若以 $i$ 为右端点的最大区间和已经用过,就pop()掉.当然,以 $i$ 为右端点的次大值也可能比剩余的都大,所以我们也要把次大值push()进去.次小值即 $sum[i]$ 减去 $max(1, i - R + 1)$ ~ $i - L + 1$ 中第二小的 $sum$. 如此往复,操作 $k$ 次. 所以我们要用主席树维护区间第 $k$ 小值. 使用算法: 堆+主席树+哈希($sum$ 太大了, 直接建树空间会炸飞).

#include<cstdio>
#include<algorithm>
#include<queue>
#define Maxn 500000
#define int long long
using namespace std;
int read() {
	int f = 1, sum = 0;
	char ch = getchar();
	while(ch < '0' || ch > '9') {
		if(ch == '-') f = -1;
		ch = getchar();
	}
	while(ch >= '0' && ch <= '9') {
		sum = sum * 10 + ch - '0';
		ch = getchar();
	}
	return f * sum;
}
void write(int x) {
	(x < 0) ? (putchar('-'), write(-x)) : (void)((x <= 9) ? (putchar(x + '0')) : (write(x / 10), putchar(x % 10 + '0')));
}
int n, k, L, R, a[Maxn + 9], ha[Maxn + 9], sss, cnt, root[Maxn + 9];
struct Emm1 {
	int num, id;
} sum[Maxn + 9];
struct Svv {
	int val, l, r;
} t[(Maxn << 5) + 9];
struct Emm2 {
	int val, id, k;
	bool operator < (const Emm2 &t) const {
		return val < t.val;
	}
};
priority_queue<Emm2> Q;
int min(int x, int y) {
	return x < y ? x : y;
}
int max(int x, int y) {
	return x > y ? x : y;
}
bool CmpNum(Emm1 x, Emm1 y) {
	return x.num < y.num;
}
bool CmpId(Emm1 x, Emm1 y) {
	return x.id < y.id;
}
void Hash() {
	sort(sum + 1, sum + n + 1, CmpNum);
	int last;
	for(int i = 1; i <= n; ++i) {
		if(i == 1 || sum[i].num != last) {
			last = sum[i].num;
			ha[++sss] = sum[i].num;
		}
		sum[i].num = sss;
	}
	sort(sum + 1, sum + n + 1, CmpId);
}
void UpDate(int &newt, int oldt, int L, int R, int p) {
	newt = ++cnt;
	t[newt] = t[oldt];
	t[newt].val++;
	if(L == R) return;
	int mid = (L + R) >> 1;
	if(p <= mid) UpDate(t[newt].l, t[oldt].l,    L   , mid, p);
	if(p  > mid) UpDate(t[newt].r, t[oldt].r, mid + 1,  R , p);
}
int Query(int p, int q, int L, int R, int k) {	
	if(L == R) {
		return L;
	}
	int tt = t[t[q].l].val - t[t[p].l].val, mid  = (L + R) >> 1;
	if(k <= tt) return Query(t[p].l, t[q].l, L, mid, k);
	if(tt < k) return Query(t[p].r, t[q].r, mid + 1, R, k - tt);
}
signed main() {
	n = read() + 1, k = read(), L = read(), R = read();
	sum[1].id = 1;
	for(int i = 2; i <= n; ++i) {
		a[i] = read();
		sum[i].num = sum[i - 1].num + a[i];
		sum[i].id = i;
	}
	Hash();
	for(int i = 1; i <= n; ++i) {
		UpDate(root[i], root[i - 1], 1, sss, sum[i].num);
	}
	for(int i = L + 1; i <= n; ++i) {
		int left = i - R, right = i - L;
		if(left < 1) left = 1;
		Emm2 ttt;
		ttt.val = ha[sum[i].num] - ha[Query(root[left - 1], root[right], 1, sss, 1)];
		ttt.id = i;
		ttt.k = 1;
		Q.push(ttt);
	}
	int ans = 0;
	for(int i = 1; i <= k; ++i) {
		Emm2 tmp = Q.top();
		Q.pop();
		ans += tmp.val;
		if(min(R - L + 1, tmp.id - L) == tmp.k) {
			continue;
		}
		int l = max(1, tmp.id - R), r = tmp.id - L;
		tmp.val = ha[sum[tmp.id].num] - ha[Query(root[l - 1], root[r], 1, sss, ++tmp.k)];
		Q.push(tmp);
	}
	write(ans);
	return 0;
}

完结撒花~

posted @ 2022-07-18 14:35 TuSalcc 阅读(102) 评论(0) 收藏举报

刷新页面返回顶部

TuSalcc

Welcome to TuSalcc's blog!

线段树