单调队列
最近学习了单调队列,在此做一个小记
单调队列(百度百科)维持了队列的单调性,是队列的一种,与队列的区别有两点:一、单调队列是单调上升或单调下降的,队列无要求。二、队列是tail进,head出,而单调队列是tail进,但head和tail都可以出(如图)。
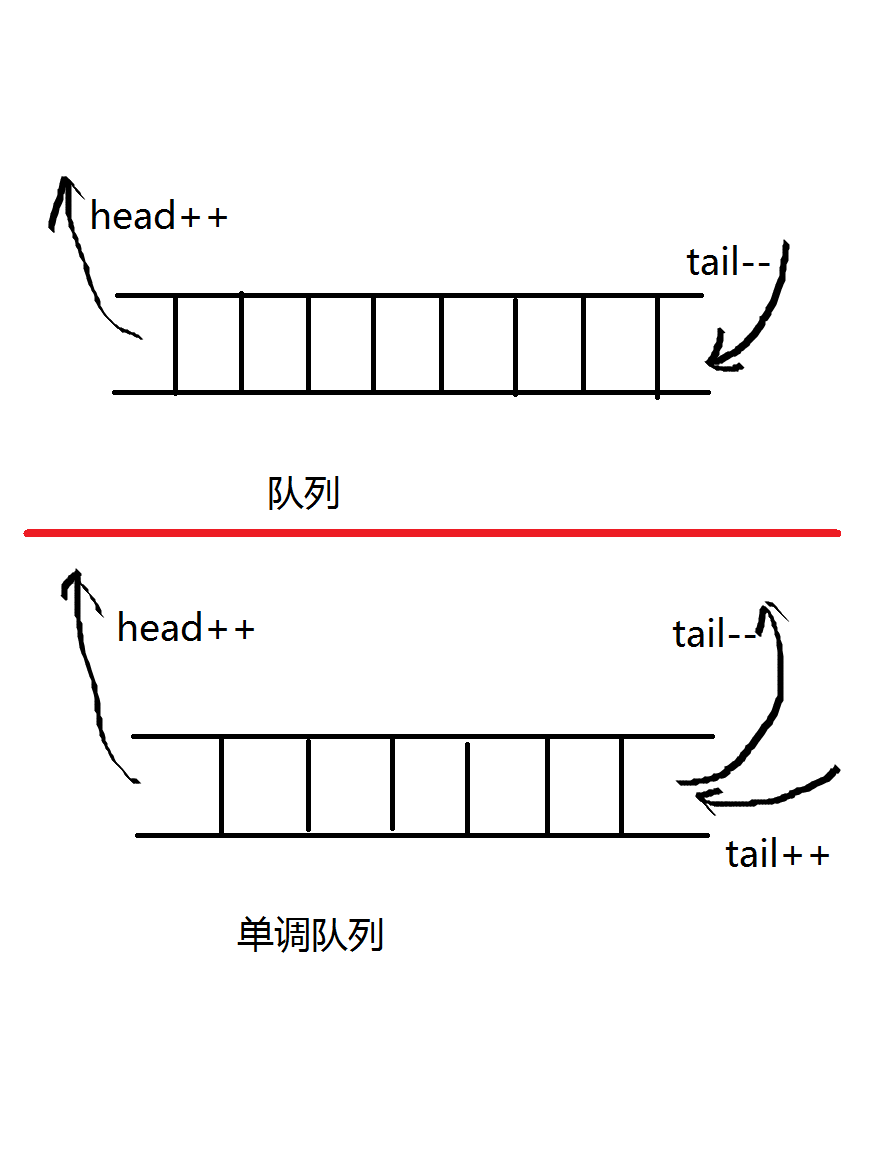
举个栗子,如果一个队列中有1,4,7,13这几个数字,这时候又来了一个5。为了维持队列的单调性,我们要先把大于5的7和13弹出,在将5压入,队列就变成了1,4,5。单调队列是以比较为基础操作的,时间复杂度是线性的。具体看模板题。
洛谷 P1886 滑动窗口 /【模板】单调队列
题目描述
有一个长为 n 的序列 a,以及一个大小为 k 的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。
例如:
The array is [1,3,−1,−3,5,3,6,7], and k = 3。
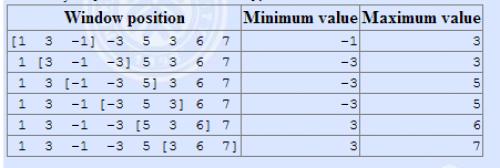
输入格式
输入一共有两行,第一行有两个正整数 n,k。 第二行 n 个整数,表示序列 a
输出格式
输出共两行,第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值
输入输出样例
输入 #1
点击查看输入
8 3
1 3 -1 -3 5 3 6 7
点击查看输出
-1 -3 -3 -3 3 3
3 3 5 5 6 7
1≤k≤n≤10^6, -231≤a[i]≤231
看到这道题最先想到的必然是暴力,时间复杂度为O(nk),明显会超时。
这道题是单调队列的模板题。以找最大值为例,如果有两个点,下标分别为i和j。如果i>j且a[i]>a[j],那么这个j就毫无用处了。因为区间是向右滑动的,所以无论如何j也不可能是最大值了。相反的,如果i<j但是a[i]<a[j]呢?这时,j是需要被保留的,因为i可能不在下个区间了。因此,在每个区间判断前,都要先把队头的不在这个区间内的弹出。以上就是思路,下面附上代码:
点击查看代码
#include<cstdio>
#include<iostream>
#include<cstring>
#define MAXN 1000000
using namespace std;
int read() {
int sum = 0, f = 1;
char ch = getchar();
while(!isdigit(ch)) {
if(ch == '-') {
f = -1;
}
ch = getchar();
}
while(isdigit(ch)) {
sum = sum * 10 + ch - '0';
ch = getchar();
}
return sum * f;
}
int a[MAXN + 9];
int q[MAXN + 9];
int n, k;
void min() {
int head = 1, tail = 0;
for(int i = 1; i <= n; ++i) {
while(head <= tail && q[head] + k < i + 1) head++;
while(head <= tail && a[i] < a[q[tail]]) tail--;
q[++tail] = i;
if(i >= k) printf("%d ", a[q[head]]);
}
}
void max() {
int head = 1, tail = 0;
for(int i = 1; i <= n; i++) {
while(head <= tail && q[head] + k < i + 1) head++;
while(head <= tail && a[i] > a[q[tail]]) tail--;
q[++tail] = i;
if(i >= k) printf("%d ", a[q[head]]);
}
}
int main() {
n = read(), k = read();
for(int i = 1; i <= n; ++i) {
a[i] = read();
}
min();
printf("\n");
memset(q, 0, sizeof(q));
max();
return 0;
}
小 Z 作为寿星,自然希望吃到的蛋糕的幸运值总和最大,但小 Z 最多又只能吃 m(m≤n) 小块的蛋糕。
请你帮他从这 n 小块中找出连续的 k(1≤k≤m) 块蛋糕,使得其上的总幸运值最大。
输入格式
第一行两个整数 n,m。分别代表共有 n 小块蛋糕,小 Z 最多只能吃 m 小块。
第二行 n 个整数,第 i 个整数 p[i] 代表第 i 小块蛋糕的幸运值。
输出格式
仅一行一个整数,即小 Z 能够得到的最大幸运值。
输入输出样例
输入 #1
点击查看输入
5 2
1 2 3 4 5
点击查看输出
9
点击查看输入
6 3
1 -2 3 -4 5 -6
点击查看输出
5
简化一下问题,就是求最大不定长字段和的问题。设f[i]为以i为右端点的最大字段和,则f[i]=max{sum[i]-sum[j] (i-m≤j≤i-1)}。其中sum为前缀和预处理,这点不难想到。观察发现,sum[i]始终为定值,所以max{sum[i]-sum[j] (i-m≤j≤i-1)}可以转化为sum[i]-min{sum[j] (i-m≤j≤i-1)}。因为每一次j的循环都花了非常多的时间,时间复杂度为O(nm),所以数据一大就会T掉,因此考虑用单调队列维护min{sum[j] (i-m≤j≤i-1)}。以上即为基本思路,下面附上代码:
点击查看代码
#include<cstdio>
#include<iostream>
#define MAXN 500000
using namespace std;
int read() {
int f = 1, sum = 0;
char ch = getchar();
while(!isdigit(ch)) {
if(ch == '-') f = -1;
ch = getchar();
}
while(isdigit(ch)) {
sum = sum * 10 + ch - '0';
ch = getchar();
}
return f * sum;
}
struct Q {
int id, sum;
};
Q q[MAXN * 2 + 9];
int sum[MAXN + 9];
int main() {
int n = read(), m = read();
for(int i = 1; i <= n; ++i) {
sum[i] = read();
sum[i] += sum[i - 1];
}
int head = 1, tail = 0;
q[++tail].id = 0;
q[tail].sum = 0;
int ans = - 1e9;
for(int i = 1; i <= n; ++i) {
while(head <= tail && q[head].id < i - m) {
++head;
}
while(head <= tail && q[tail].sum >= sum[i]) {
--tail;
}
ans = max(ans, sum[i] - q[head].sum);
q[++tail].id = i;
q[tail].sum = sum[i];
}
printf("%d", ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号