北京地铁最短路径规划

地铁最短路径

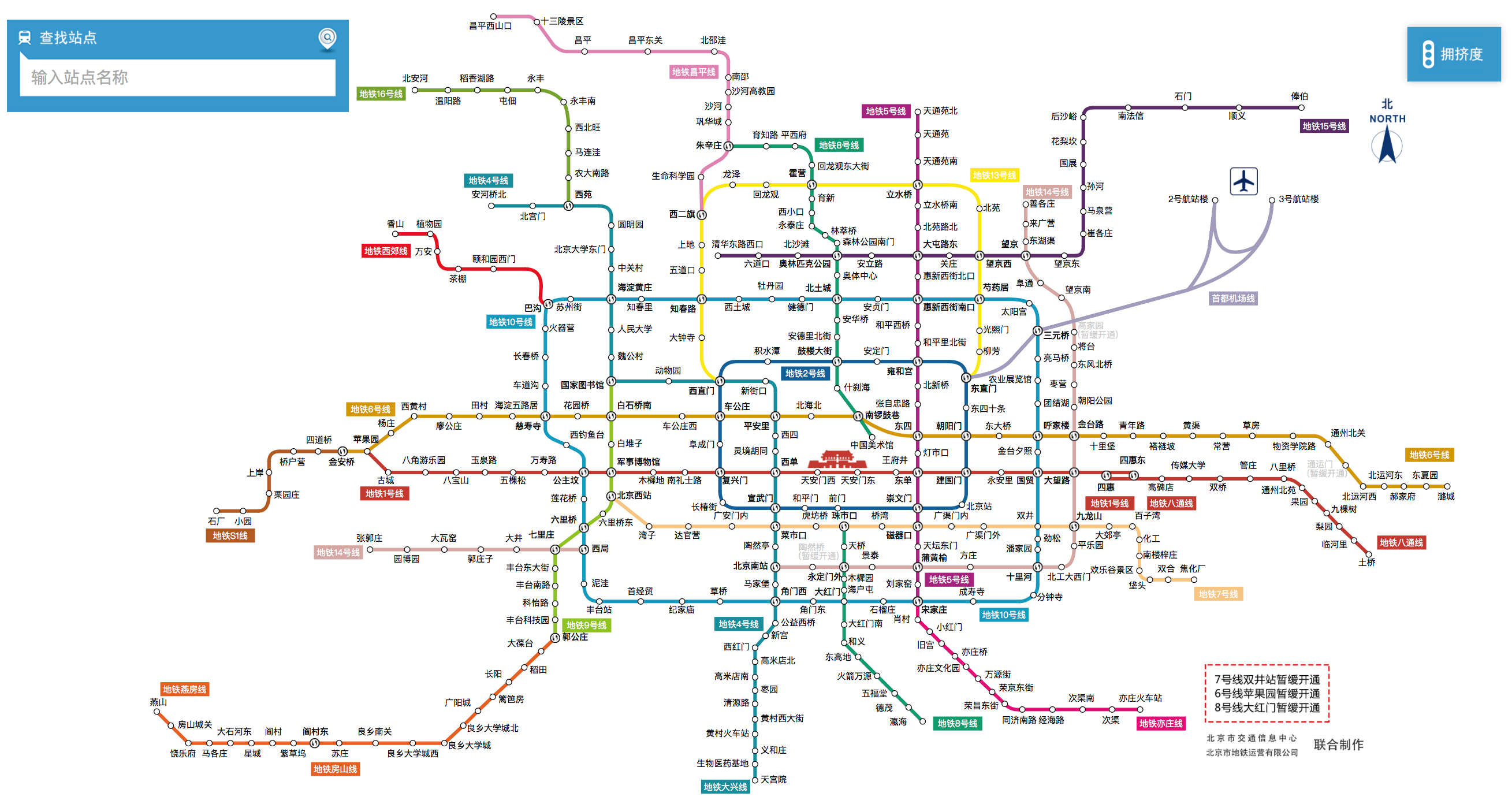
1、问题重述

提供一副地铁线路图，计算指定两站之间最短（最少经过站数）乘车路线；输出指定地铁线路的所有站点。以北京地铁为例，地铁线路信息保存在data.txt中，格式如下：

地铁线路总数
线路名1 站名1 站名2 站名3 ...
线路名2 站名1 站名2 站名3 ...
线路名3 站名1 站名2 站名3 ......

实现以下功能：

实现地铁线路信息图的导入
实现查询功能，查询指定地铁线路之间的信息
实现从出发地到目的地之间最短路径规划，并供使用者使用

2、实现语言

　　java

3、实现算法

　　Floyd算法

Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与Dijkstra算法类似。

通过一个图的权值矩阵求出它的每两点间的最短路径矩阵。

从图的带权邻接矩阵A=[a(i,j)] n×n开始，递归地进行n次更新，即由矩阵D(0)=A，按一个公式，构造出矩阵D(1)；又用同样地公式由D(1)构造出D(2)；……；最后又用同样的公式由D(n-1)构造出矩阵D(n)。矩阵D(n)的i行j列元素便是i号顶点到j号顶点的最短路径长度，称D(n)为图的距离矩阵，同时还可引入一个后继节点矩阵path来记录两点间的最短路径。

采用松弛技术（松弛操作），对在i和j之间的所有其他点进行一次松弛。所以时间复杂度为O(n^3);
其状态转移方程如下： map[i,j]:=min{map[i,k]+map[k,j],map[i,j]}；

map[i,j]表示i到j的最短距离，K是穷举i,j的断点，map[n,n]初值应该为0，或者按照题目意思来做。

当然，如果这条路没有通的话，还必须特殊处理，比如没有map[i,k]这条路。

4、类职责划分（相关类的功能描述）

FileRead:主要负责文本的读入，包含一个方法

public List<Station> readText(String Path)

Station：用于储存站点，包含对应变量的set和get方法

StationMap：用于储存Floyd算法中将会用到的图的邻接矩阵，即地铁站点图，除相应的get和set方法外，还包括以下方法

public void insertEdge(T start, T stop, int weight)//插入边
public void removeEdge(String start, String stop)//删除边
public StringBuilder findByFloyd(T start, T stop,int[][] sub,List<Station> allroute)//输入起始点和终点，调用Floyd算法
public String findsameStation(String s1,String s2,List<Station> allroute)//寻找相同站点

Floyd：Floyd算法的具体实现
Main：主要的交互界面，并且输出最终结果，以文本形式保存

5、核心代码

(1)FileRead

package FileRead;

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.StringReader;
import java.util.ArrayList;
import java.util.List;

import Model.Station;

public class ReadTxt {
     public List<Station> readText(String Path){
          List<Station> allroute=new ArrayList<Station>();
          try {
              String obtain = " ";//分割符号
              File file=new File(Path);
              //判断文件是否存在
              if(file.isFile() && file.exists()){ 
                  InputStreamReader reader = new InputStreamReader(new FileInputStream(file));
                  BufferedReader bufferedReader = new BufferedReader(reader);
                  String stationline = null;
                  while((stationline = bufferedReader.readLine()) != null){       
                      //分割字符串
                      Station station=new Station();
                      String string="";    
                      String tmp[] = stationline.split(obtain);
                      string=tmp[0];
                      station.setStationNo(string);
                      List<String> allstation=new ArrayList<>();
                      //遍历后加入站点
                      for(String s:tmp) {
                          allstation.add(s);
                      }
                      allstation.remove(0);
                      station.setAllStation(allstation);
                      allroute.add(station);
                  }
                 // 关闭文件
                  reader.close();
                  bufferedReader.close();
              }
              else
                  System.out.println("找不到指定的文件!");
            } catch (Exception e) {
                System.out.println("文件内容出错!");
                e.printStackTrace();
             }
//          System.out.println("读入文件结束！");
          return allroute;
         }
}

(2)station

package Model;

import java.util.ArrayList;
import java.util.List;

public class Station {
    public String stationNo;
    public List<String> allStation=new ArrayList<String>();
    
    public String getStationNo() {
        return stationNo;
    }
    public void setStationNo(String stationNo) {
        this.stationNo = stationNo;
    }
    public List<String> getAllStation() {
        return allStation;
    }
    public void setAllStation(List<String> allStation) {
        this.allStation = allStation;
    }
    
}

(3)stationmap（仅展示相对重要部分）

//MAX_WEIGHT为定义的最大边长，最大值为100
public void insertEdge(T start, T stop, int weight) { 
        int n = subTrainMatrix.length;
        int i = getPosInvertex(start);
        int j = getPosInvertex(stop);
        if (i >= 0 && i < n && j >= 0 && j < n
                && this.subTrainMatrix[i][j] == MAX_WEIGHT && i != j) {
            this.subTrainMatrix[i][j] = weight;
            this.subTrainMatrix[j][i] = weight;
        }
    }
public void removeEdge(String start, String stop) { 
        int i = vertex.indexOf(start);
        int j = vertex.indexOf(stop);
        if (i >= 0 && i < vertexCount() && j >= 0 && j < vertexCount()
                && i != j)
            this.subTrainMatrix[i][j] = MAX_WEIGHT;
    }
public StringBuilder findByFloyd(T start, T stop,int[][] sub,List<Station> allroute) {
        List<String> change=new ArrayList<>();
        Floyd floyd = new Floyd(sub);
        int startPos = getPosInvertex(start);
        int stopPos = getPosInvertex(stop);
        int[] path = floyd.getPath(startPos, stopPos);
        StringBuilder sb = new StringBuilder();
        System.out.print(start + " 到 " + stop + " 的路线为: ");
        sb.append(start + " 到 " + stop + " 的路线为: ");
        int k=0;
        for (int i : path) {
            k++;
            sb.append(vertex.get(i) + " --> ");
            if(k%5==0) {
                sb.append(System.lineSeparator());
            }
        }
        sb.delete(sb.lastIndexOf(" --> "), sb.length());
        
        for(int j=1;j<(path.length)-1;j++) {
            int i=path[j];
            
            String s1=findsameStation(vertex.get(path[j-1])+"", vertex.get(i)+"", allroute);
            String s2=findsameStation(vertex.get(i)+"", vertex.get(path[j+1])+"", allroute);
            if(!s1.equals(s2)) {
                change.add(vertex.get(i)+"");
            }
        }
        System.out.println(sb.toString());
        System.out.println("换乘站:");
        sb.append(System.lineSeparator()+"换成站:"+System.lineSeparator());
        for(String s:change) {
            System.out.println(s);
            sb.append(s+System.lineSeparator());
        }
        System.out.println(start + " -> " + stop + " 经过的站点数为： " + path.length);
        sb.append(start + " -> " + stop + " 经过的站点数为： " + path.length);
        
        
        return sb;

    }
public String findsameStation(String s1,String s2,List<Station> allroute) {
        String route="";
        List<String> routes1=new ArrayList<>();
        List<String> routes2=new ArrayList<>();
        for(Station r:allroute) {
            for(String s:r.getAllStation()) {
                if(s.equals(s1)) 
                    routes1.add(r.getStationNo());
                if(s.equals(s2)) 
                    routes2.add(r.getStationNo());
            }
        }
        for(int i=0;i<routes1.size();i++) 
            for(int j=0;j<routes2.size();j++) 
                if(routes1.get(i).equals(routes2.get(j))) 
                    route=routes1.get(i);
        return route;
    }

(4)Floyd（核心算法部分）

public Floyd(int[][] G) {
        // 图G的行数
        int row = G.length;
        // 定义任意两点之间经过的点
        int[][] spot = new int[row][row];
        // 记录一条路径
        int[] onePath = new int[row];
        this.length = G;
        path = new int[row][row][];
        for (int i = 0; i < row; i++)
            // 初始化
            for (int j = 0; j < row; j++)
                spot[i][j] = -1;
        for (int i = 0; i < row; i++)
            // 假设任意两点之间的没有路径
            onePath[i] = -1;
        for (int u = 0; u < row; ++u)
            for (int v = 0; v < row; ++v)
                for (int w = 0; w < row; ++w)
                    if (length[v][w] > length[v][u] + length[u][w]) {
                        // 如果存在更短路径则取更短路径
                        length[v][w] = length[v][u] + length[u][w];
                        spot[v][w] = u;
                    }
        for (int i = 0; i < row; i++) {
            int[] point = new int[1];
            for (int j = 0; j < row; j++) {
                point[0] = 0;
                onePath[point[0]++] = i;
                // 更新路径
                outputPath(spot, i, j, onePath, point);
                path[i][j] = new int[point[0]];
                for (int s = 0; s < point[0]; s++)
                    path[i][j][s] = onePath[s];
            }
        }
    }