忘光了，所以复习【GEO】

计算几何

感谢 zjb 的大力支持。参考复制自 zjb 课件。

基础知识

向量

向量是具有方向和大小的量，一个 \(k\) 维空间中的向量 \(\vec{a}\) 可以用一个 \(k\) 元组 \((a_1,\cdots,a_k)\) 表示，在平面几何中亦可用角度与模长 \((\alpha,\theta)\) 表示。零向量是没有方向，模长为 \(0\) 的向量。

\(k\) 维向量（记为 \(\vec{x}\)）也可以表示为一个 \(k\times 1\) 的矩阵：

\[ \begin{bmatrix} a_1 \\ \vdots \\ a_k \\ \end{bmatrix} \]

记一个 \(\vec{x}\) 的模长为 \(|\vec{x}|\)，有 \(|\vec{x}|=\sqrt{\sum\limits_{i=1}^ka_i^2}\)

向量基本运算

• 加法：\((a_1,\cdots,a_k)+(b_1,\cdots,b_k)=(a_1+b_1,\cdots,a_k+b_k)\)

• 数乘：\(\lambda\cdot(a_1,\cdots,a_k)=(\lambda a_1,\cdots,\lambda a_k)\)

• 点积：\((a_1,\cdots,a_k)\cdot(b_1,\cdots,b_k)=a_1\times b_1+\cdots+a_k\times b_k\)

• 叉积仅在二维和三维向量下有定义：

  • 二维：\((x_a,y_a)\times(x_b,y_b)=x_ay_b-y_ax_b\)

  • 三维：

    \[ (x_a,y_a,z_a)\times(x_b,y_b,z_b)= \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ x_a & y_a & z_a \\ x_b & y_b & z_b \\ \end{vmatrix} \]

    其中 \(\hat{\imath},\hat{\jmath},\hat{k}\) 分别是三维的单位向量。

• 由上面的运算我们还可以定义出 \(-\vec{a}=(-1)\cdot\vec{a},\vec{a}-\vec{b}=\vec{a}+(-\vec{b})\)。

向量运算的一些性质

• \(\vec{a}+\vec{b}=\vec{b}+\vec{a}\)
• \((\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})\)
• \(\lambda\cdot(\vec{a}+\vec{b})=\lambda\cdot\vec{a}+\lambda\cdot\vec{b}\)
• \((\lambda+\mu)\cdot\vec{a}=\lambda\cdot\vec{a}+\mu\cdot\vec{a}\)
• \(\lambda\cdot\vec{a})\cdot\vec{b}=\lambda\cdot(\vec{a}\cdot\vec{b})=\vec{a}\cdot(\lambda\cdot\vec{b})\)
• \(\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}\)
• \(\vec{a}\cdot(\vec{b}+\vec{c})=\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}\)
• \(\vec{a}\times\vec{a}=0\)
• \(\vec{a}\times\vec{b}=-\vec{b}\times\vec{a}\)
• \((\lambda\cdot\vec{a})\times\vec{b}=\lambda\cdot(\vec{a}\times\vec{b})=\vec{a}\times(\lambda\cdot\vec{b})\)

向量加法

向量的加法满足平行四边形法则和三角形法则。

向量数乘

向量的数乘相当于伸长或压缩，在 \(\lambda\cdot\vec{a}\) 中：

当 \(\lambda>0\) 时，相当于在原方向等比例伸长或压缩 \(\vec{a}\) 至原来的 \(\lambda\) 倍。

当 \(\lambda=0\) 时，相当于变为零向量。

当 \(\lambda<0\) 时，相当于在反方向等比例伸长或压缩 \(\vec{a}\) 至原来的 \(\lambda\) 倍。

向量点积

向量的点积的结果的几何意义是一个向量在另一个向量所在的数轴的投影的有向长度乘以另一个向量的模长。

因此还有 \(\vec{a}\cdot\vec{b}=|\vec{a}|\cdot|\vec{b}|\cdot\cos\theta\) ，其中 \(\theta\) 是从 \(\vec{a}\) 以逆时针方向到 \(\vec{b}\) 的夹角。

还有一个优美的物理意义：一个物体在力 \(F\) 的作用下产生位移 \(s\)，那么 \(F\) 做的功为 \(|F||s|\cos \theta\)，\(\theta\) 为 \(F\) 与 \(s\) 的夹角。

由几何意义还可以得出 \(\vec{a}\cdot\vec{b}=0\Leftrightarrow\vec{a}\perp\vec{b}\)。

几何意义的得出可以参考 @3Blue1Blown 的视频。

向量叉积

二维向量的叉积的结果的几何意义是两个向量为相邻两边，组成的平行四边形的有向面积。

\(\vec{a}\) 以逆时针方向到 \(\vec{b}\) 的夹角不超过 \(\pi\) 时，\(\vec{a}\times\vec{b}\geq0\) 。

因此还有 \(\vec{a}\times\vec{b}=|\vec{a}|\cdot|\vec{b}|\cdot\sin\theta\) ，其中 \(\theta\) 是从 \(\vec{a}\) 以逆时针方向到 \(\vec{b}\) 的夹角。

由几何意义还可以得出 \(\vec{a}\times\vec{b}=0\Leftrightarrow\vec{a}\parallel\vec{b}\) 。

基础应用

判断点在直线的哪边

已知有向直线 \(AB\) ，求点 \(O\) 与 \(AB\) 的相对关系。

注意到叉积的性质，因此可以使用 \(x=\vec{AO}\times\vec{AB}\) 的符号来判断。

• \(x>0\) 时，点 \(O\) 在有向直线 \(AB\) 的逆时针方向。
• \(x=0\) 时，点 \(O\) 在有向直线 \(AB\) 上。
• \(x<0\) 时，点 \(O\) 在有向直线 \(AB\) 的顺时针方向。

判断两线段是否相交

给定两条线段，判断它们之间是否有交。

判断两线段是否相交有一个非常常用的方法，即使用快速排斥实验和跨立实验进行判断。当且仅当两个实验均成功时，两线段相交。

快速排斥实验：判断两条线段所成矩形是否有交，即在 \(x\) 轴和 \(y\) 轴上是否同时有交集。

跨立实验：判断对两条线段分别进行一次判断，判断一条线段的两个端点是否在另一条线段的不同边。

判断一点是否在多边形内部

给定一个点和一个有 \(n\) 个点的多边形，判断这个点是否在多边形内部。

显然一点在一个多边形内的充要条件是从该点任意方向射出一条射线，与多边形的交点数为奇数。

因此射条射线出来，判断与多边形的交点数量即可。

时间复杂度 \(O(n)\) 。

不方便处理点在多边形上，多边形有圆弧，或者射线卡在（自交）多边形角上的情况。

用一个点绕着多边形转一圈，看这个点在这个过程中相对于给定点转过的度数。

实现时因为浮点误差原因不直接计算角度，而是计算其顺时针和逆时针穿过一条从给定点引出的射线几次，将逆时针看做 +1，顺时针看做 -1，统计出绕数。若其为 0 则表明转角和为 0。

求两条直线的交点

给定直线 \(AB\) 和 \(CD\) ，求直线 \(AB\) 和 \(CD\) 的交点 \(O\) 。

求交点的推法有很多，这里简单介绍一种。

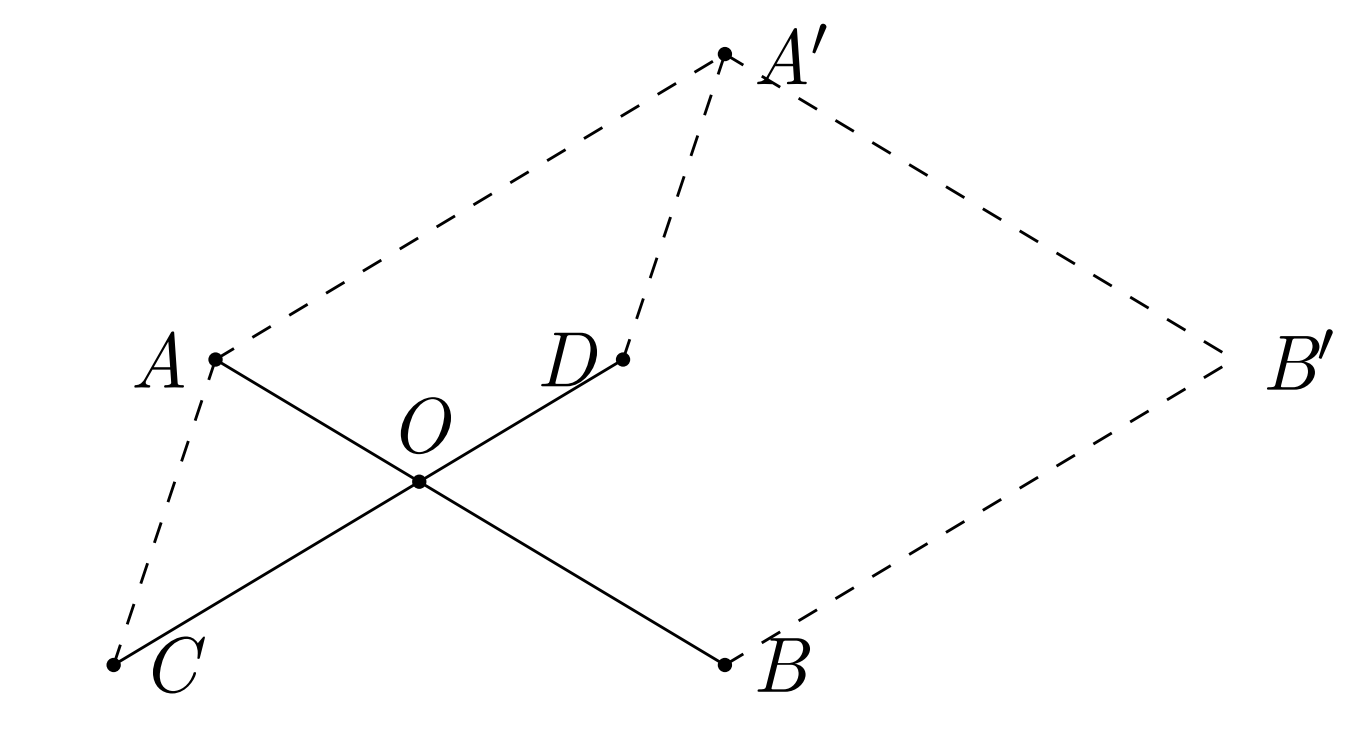
\(\frac{S_{▱{ACDA'}}}{S_{▱{ABB'A'}}}=\frac{\vec{CD}\times\vec{CA}}{\vec{AB}\times\vec{CD}}=\frac{|\vec{AO}|}{|\vec{AB}|}\Rightarrow\vec{AO}=\frac{\vec{CD}\times\vec{CA}}{\vec{AB}\times\vec{CD}}\cdot\vec{AB}\)

然后用 \(A\) 的坐标加上 \(\vec{AO}\) 即可。

求圆过圆外一点的切线

因为方程过于复杂，考虑不使用解方程的方法。

我们以 \(O\) 为原点，\(\vec{c}\) 为 \(x\) 轴正方向，与 \(x\) 轴正交的任意一个向量作为 \(y\) 轴正方向。

不难发现 \(\overrightarrow{a}\) 可以拆成两个基向量线性组合的形式。

设 \(|\overrightarrow{d}|=|\overrightarrow{c}|\) 且 \(\overrightarrow{c}\cdot\overrightarrow{d}=0\) ，则 \(\overrightarrow{a}=\frac{\overrightarrow{a}^2}{\overrightarrow{c}^2}\cdot\overrightarrow{c}\pm\frac{\overrightarrow{a}\times\overrightarrow{b}}{\overrightarrow{c}^2}\cdot\overrightarrow{d}\) 。

式子中的值均可以轻松算出，因此即得：

\[ \overrightarrow{a}=\frac{\overrightarrow{a}^2\cdot\overrightarrow{c}\pm\overrightarrow{a}\times\overrightarrow{b}\cdot\overrightarrow{d}}{\overrightarrow{c}^2} \]

向量旋转

• 向量 \((x,y)\) 逆时针旋转 \(\alpha\) 后变为 \((x',y')\)。
• 那么 \(x'=x\cos\alpha -y\sin \alpha,y'=x\sin\alpha + y\cos\alpha\)。

面积相关

三角形面积

\[\begin{aligned} S_{\triangle{ABC}} & =\frac{ah}{2} \\ & =\frac{\sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)}}{4} \\ & =\frac{ab\sin{C}}{2} \\ & =\frac{(a+b+c)r}{2} \\ & =\frac{abc}{4R} \\ & =2R^2\sin{A}\sin{B}\sin{C} \\ & =\frac{\left|\vec{a}\times\vec{b}\right|}{2} \\ \end{aligned} \]

多边形面积

• 容易把多边形分成若干个有向三角形。
• 然后把面积加起来。

求多边形内部整点数量

• 按逆时针顺序给定一个点数为 \(n\) 的多边形的每个点 \({P_0,\cdots,P_{n-1}}\) ，求其内部整点数量。
• 先给出皮克定理：
  • 以整点为顶点的多边形面积 \(S\) 、边上整点数 \(a\) 和内部整点数 \(b\) 的关系式为：\(S=\frac{a}{2}+b-1\) 。
• 因此我们可以算出面积和边上格点数目后即可套用皮克定理算出内部整点数。

凸包

• 在一个实数向量空间 \(V\) 中，对于给定集合 \(X\) ，所有包含 \(X\) 的凸集的交集 \(S\) 被称为 \(X\) 的凸包。\(X\) 的凸包可以用 \(X\) 内所有点 \((X_1,\cdots,X_n)\) 的凸组合来构造。

通俗地说，凸包就是面积最小的能包住所有给定点的凸多边形。

凸包在优化动态规划和平面几何等问题中有着重要的作用。

下面简单给出两种求凸包的方式。

求点集的凸包

Andrew 算法

求出上凸壳和下凸壳，然后合并即可得到凸包。

凸壳我们可以直接按 \(x\) 作关键字排序后使用单调栈维护答案，斜率不单调时弹出栈。

最后单调栈中的点即为凸壳上的点按顺序排列的结果。

时间复杂度 \(O(n\log n)\) 。

Graham 算法

先找到 \(y\) 最小且 \(x\) 相对较小的点 \(C\) 。

然后把所有点进行排序，关键字为点 \(C\) 与其所成直线的斜率。

随后使用单调栈维护，斜率不单调时弹出栈。

最后单调栈中的点即为凸包上的点按顺序排列的结果。

时间复杂度 \(O(n\log n)\) 。

三维凸包

三维凸包是指给定一组三维空间中的点，找到一个最小的凸多面体，使得所有的点都在其内部或者表面上。三维凸包可以用来描述物体的形状、计算物体的体积、检测物体之间的碰撞等。

求解三维凸包有很多算法，其中比较常用和高效的有增量法、分治法和快速凸包法。这些算法都基于以下思想：从一个初始的凸多面体开始，逐步添加新的点，并更新凸多面体，直到所有点都被处理完毕。

增量法是最简单和直观的一种方法，它从一个初始的四面体开始（如果四个点共面，则需要微小扰动），每次添加一个新点时，检查它是否在当前凸多面体内部。如果在内部，则不需要更新；如果在外部，则需要删除所有与该点可见（即构成正向锥形）的面，并添加新生成的面。这个过程重复直到所有点都被处理完毕。

\(O(n^2)\)。

旋转卡壳

一种高效的解决最优化问题的思想。

这个思想非常类似于 two pointers（枚举一个指针，另一个指针滑动，一般用于解决序列问题的思想）。

枚举点/边，然后去维护当前点/边的最优点/边，并计算答案。

由于在一些题目中，最优点/边是单调的，因此这个思想可以快速地求解。

半平面交

显然答案就是由所有直线的一部分形成的一个凸多边形或凸壳。

一般情况下题目会保证结果是一个凸多边形，如果答案可能是凸壳，可以在平面的四边加入四个半平面来保证其形成凸多边形。

接下来默认直线为有向直线，且所有直线给定的半平面均为其逆时针方向一侧。

先将所有的直线以其向量的幅角为关键字进行排序，若幅角相等，删除限制更弱的。

接下来类似求凸包，但是插入的内容变成了直线。

维护两个双端队列，一个维护在答案凸多边形上的直线，一个维护答案凸多边形上相邻直线的交点。

依次插入直线，执行下列操作：

弹出队尾的直线，重复直到队列中的直线数量不足两条或队尾两条直线的交点在当前插入直线的逆时针侧为止。

弹出队首的直线，重复直到队列中的直线数量不足两条或队首两条直线的交点在当前插入直线的逆时针侧为止。

将直线插入至队尾。

为什么要先弹出队尾后弹出队首？

首先在弹出队列前，哪些点需要弹出就已经确认，区别无非是弹出点左边的直线还是右边的直线而已。

根据条件易知，当队列中的点不是全部需要弹出时，先后顺序无所谓。

因此唯一会导致答案错误的情况就是所有点均需要弹出。

而所有点均需要弹出的情况非常显然，只需要保留第一条直线。

判断半平面交是否有解

• 给定一个多边形，询问其是否存在核。
  核：多边形内部的一个极大区域，使得区域中任意一个点 \(A\) 均满足：对于任意该多边形内的点 \(B\) ，两点之间的线段 \(AB\) 均与该多边形无交点。

  不难发现核可以通过将多边形的每条边作为半平面，然后作半平面交得到。

  因此求半平面交即可。

  但是难点在于如何判断半平面交是否有解。

  先加入一个极大正方形，使得半平面交的面积不可能为 \(+\infty\) 。

  考虑若一个半平面交无解，显然在其构造过程中，存在一个半平面满足之前的所有交点均不在其中。

  然而这不是充分条件，还有这两种情况是可能有解的：
  

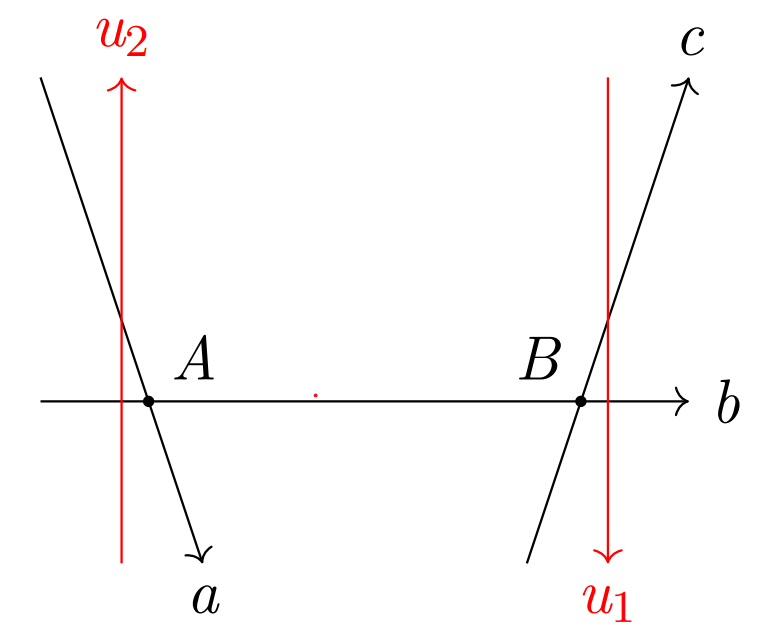
​ 不难发现这两种情况就是弹队列最后剩下的半平面和加入的半平面的极角差还没超过 \(\pi\) ，加个条件即可。

最近点对

平面最近点对

给定平面中若干点，求距离最近的点对。

考虑使用分治法，首先对所有点按 \(x\) 为关键字排序。

每次将所有点按照 \(x=mid\) 平均分成两半，先递归算出两边的答案，随后可以得到一个当前答案 \(d\) 。

接着只考虑 \(x\in\left[mid-d,mid+d\right]\) 的点，把这些点按照 \(y\) 从小到大排序并枚举。

由于任意两个属于同一边的点的距离均不小于 \(d\) ，因此点分布是稀疏的。

如图，易知正方形内最多只有四个点，因此每个点仅需与另一边至多四个点计算。

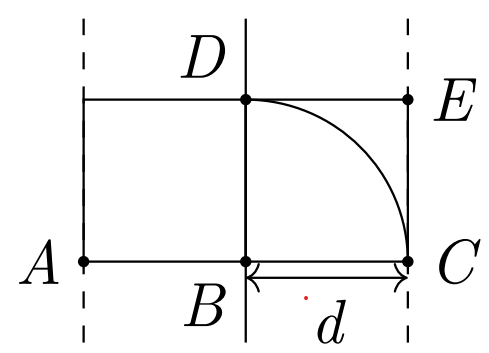
时间复杂度 \(O(n\log n)\) 。

其实不用算四个点，算两个点就够了。

考虑证明 \(y\) 坐标较大的两个点才有可能成为被计算的点。

反证。

空间最近点对

给定空间中若干点，求距离最近的点对。

思路与平面最近点对类似，设按 \(z=mid\) 分割后分治的答案为 \(d\) ，然后留下 \(z\in\left[mid-d,mid+d\right]\) 的点。

枚举左部点，考虑右部点对左部点的贡献。

我们可以把所有点投影到 \(z=mid\) 这个平面上，此时左部点 \((x_l,y_l,z_l)\) 只需要和投影后 \(x_r\in\left[x_l-d,x_l+d\right],y_r\in\left[y_l-d,y_l+d\right]\) 的右部点计算答案，这是一个正方形，可以使用扫描线维护。

可以证明，每个左部点最多仅需要与 \(O(1)\) 个点计算答案，证明可见 空间最近点对的计算机算法研究（胡金初、张晓红）。

时间复杂度 \(O(n\log^2n)\) 。

欧拉公式

• 对于任意多面体，其点数 \(V\) ，边数 \(E\) 和面数 \(F\) 的关系式为：\(V-E+F=2\) 。

上述定理亦可以在二维中得到体现。

可以将二维平面中的无限面积面视为从非无限面积面的背面绕过去，形成的一个多面体，从而得到：

• 对于任意平面图，其点数 \(V\) 、边数 \(E\) 、面数 \(F\) 和联通块数 \(U\) 的关系式为：\(V-E+F-U=1\) 。

随机增量法

增量法的思想与数学归纳法类似，它的本质是将一个问题化为规模刚好小一层的子问题。写成递归式是：\(T(n)=T(n-1)+g(n)\)。

增量法形式简洁，可以应用于许多的几何题目中。

增量法往往结合随机化，可以避免最坏情况的出现。

判断半平面交是否有解

给定一个多边形，询问其是否存在核。

之前我们用半平面交解决了这题，但是也可以用随机增量法，代码量更小。

打乱半平面的顺序，初始解可为任意点。

按打乱后的顺序加入半平面。若当前解不在当前加入的半平面内，以以下方式求出新解：

将当前加入的半平面对应的直线视为一条数轴，每个已加入的半平面限制解必须位于 \((-\infty,x]\) 或 \([x,+\infty)\) 。

求出已加入半平面对应的区间的交，取交中点 \(y\) 坐标最小的点作为当前的新解，或者交为空，说明无解。

显然该算法的复杂度上界为 \(O(n^2)\) ，接下来我们证明其在随机顺序的半平面下复杂度为 \(O(n)\) 。

设 \(p(i)\) 为加入第 \(i\) 个半平面时，当前解变为不合法的概率，则算法的期望时间复杂度 \(\displaystyle T(n)=\sum_{i=1}^nO(i) p(i)\) 。

假设当前解在加入第 \(i\) 个半平面后变为不合法，则新解一定在第 \(i\) 条直线上，由于新解是前 \(i\) 个半平面的交中 \(y\) 轴最小的，而且仅由两个半平面就可以确定这个点，因此这两个半平面里，其中一个是第 \(i\) 个半平面的概率 \(p(i)=\frac{2}{i}\) ，因此期望时间复杂度 \(T(n)=\displaystyle\sum_{i=1}^nO(i) p(i)=\sum_{i=1}^n\frac{2}{i}O(i)=O(n)\) 。

最小圆覆盖

在一个平面上有 \(n\) 个点，求一个半径最小的圆，能覆盖所有的点。

定理：如果点 \(p\) 不在集合 \(S\) 的最小覆盖圆内，则 \(p\) 一定在 \(S\cup {p}\) 的最小覆盖圆上。

假设圆 \(O\) 是前 \(i-1\) 个点的最小覆盖圆，加入第 \(i\) 个点，如果在圆内或边上则什么也不做。否则，新得到的最小覆盖圆肯定经过第 \(i\) 个点。

然后以第 \(i\) 个点为基础（半径为 \(0\)），重复以上过程依次加入第 \(j\) 个点，若第 \(j\) 个点在圆外，则最小覆盖圆必经过第 \(j\) 个点。

重复以上步骤。（因为最多需要三个点来确定这个最小覆盖圆，所以重复三次）遍历完所有点之后，所得到的圆就是覆盖所有点得最小圆。

在最开始的时候先打乱点集。

由于一堆点最多只有 \(3\) 个点确定了最小覆盖圆，因此 \(n\) 个点中每个点参与确定最小覆盖圆的概率不大于 \(\frac 3n\)，所以，每一层循环在第 \(i\) 个点处调用下一层的概率不大于 \(\frac 3i\)。

令 \(3\) 个循环复杂度依次为 \(O(n),O(n),O(n)\)，所以是对的。

反演

给定反演中心点 \(O\) 和反演半径 \(R\)。若平面上点 \(P\) 和 \(P'\) 满足：

• 点 \(P'\) 在射线 \(\overrightarrow{OP}\) 上。
• \(|OP| \cdot |OP'| = R^2\) 则称点 \(P\) 和点 \(P'\) 互为反演点。

一个图形的反演即为该图形每个点在极限意义下的反演点所构成的图形。

Problem of Apollonius

给定两个圆和一个点，求所有过 \(O\) 点，与两个圆均相切的圆。

因为是圆切圆，所以考虑以 \(O\) 为中心，任意半径进行反演。

不难发现，在新的反演平面上，求答案从圆变成了直线。

三角剖分

三角剖分：假设 \(V\) 是二维实数域上的有限点集，边 \(e\) 是由点集中的点作为端点构成的封闭线段, \(E\) 为 \(e\) 的集合。那么该点集 \(V\) 的一个三角剖分 \(T=(V,E)\) 是一个平面图 \(G\)，该平面图满足条件：

• 除了端点，平面图中的边不包含点集中的任何点。
• 没有相交边。
• 平面图中所有的面都是三角面，且所有三角面的合集是散点集 \(V\) 的凸包。

Delaunay 三角剖分

对于一个点集 \(P\) ，其 Delaunay 三角剖分（简称 DT ）\(\text{DT}(P)\) 满足：

1. 空圆性：若点集 \(P\) 中不存在四点共圆，则 \(\text{DT}(P)\) 唯一，且任意划分出的三角形的外接圆内皆不存在其它点。
2. 最大化最小角：在点集 \(P\) 的所有合法三角剖分中，\(\text{DT}(P)\) 所划分出的所有三角形的最小角最大。即不存在其它三角剖分的所有三角形的最小角大于 \(\text{DT}(P)\) 。\(\text{DT}(P)\) 是最接近于规则化的三角剖分，即两个相邻的三角形构成的凸四边形的对角线若改变，两个内角的最小角不再增大。

性质

1. 最接近：以最接近的三点形成三角形，且各线段（三角形的边）皆不相交。
2. 唯一性：不论从区域何处开始构建，最终都将得到一致的结果（点集中任意四点不能共圆）。
3. 最优性：任意两个相邻三角形构成的凸四边形的对角线如果可以互换的话，那么两个三角形六个内角中最小角度不会变化。
4. 最规则：如果将三角剖分中的每个三角形的最小角进行升序排列，则 Delaunay 三角剖分的排列得到的数值最大。
5. 区域性：新增、删除、移动某一个顶点只会影响邻近的三角形。
6. 具有凸边形的外壳：三角剖分最外层的边界形成一个凸多边形的外壳。

构造方法

按 \(x\) 轴第一关键字，\(y\) 第二关键字排序。

在点的标号上分治（注意不是坐标）。

可以发现，最后一定会成为 \(2\) 或 \(3\)，立刻形成线段或三角形。

怎么合并呢？

不难发现，我们在合并过程中不会增加两边点集的内部边，但有可能删除一些边。

从两侧选择一对连边后边不与已有的边相交且 \(y\) 最小的点作为当前初始点 \(L,R\)，将这两个点连边。

具体的，先随便钦定为 \(y\) 最小两个点，每次遍历邻边，如有较原来更优的点就更新。

执行下列操作直到无法操作为止：

• 分别确定两侧的下一个顶点，将从当前点出发可达的点一一尝试，若一个点与 \(L,R\) 的外接圆内不包含任何其它点，则该点成为该侧的下一个顶点，可以证明在没有四点共圆的情况下没有多个这样的顶点。
• 与下一个顶点同侧的当前点转变为下一个顶点，并在两个当前点之间连一条线段，消除所有与其有交的线段。

Anti-DT

顾名思义。对于一个点集 \(P\) ，其 Anti-Delaunay 三角剖分（简称 ADT ） \(\text{ADT}(P)\) 满足：

1. 满圆性：若点集 \(P\) 中不存在四点共圆，则 \(\text{ADT}(P)\) 唯一，且任意划分出的三角形的外接圆外皆不存在其它点。

Voronoi 图

最近点 Voronoi 图由连接两邻点直线的垂直平分线组成的连续多边形组成。

最近点 Voronoi 图中每个点占有一个区域，这个区域即这个点和每个点的垂直平分线靠近这个点一侧的半平面交。

Voronoi 图与 Delaunay 三角剖分互为对偶图。

题

「ZJOI2018」保镖

平面上有 \(n\) 个点，给定一个矩形，求随机从矩形中随机一个点作为反演中心后所有点的凸包的期望点数是多少。
\(1\leq n\leq 2000\) ，保证精度足够。

凸包数量不好求，我们用欧拉公式转化一下。

设反演后的 Delaunay 三角剖分中，凸包上边数为 \(V_1\) ，不在凸包上的边数为 \(V_2\) ，三角形数量为 \(T\) ，则有：

\[\begin{cases} V_1+2V_2=3T \\ n-(V_1+V_2)+(T+1)=2 \\ \end{cases} \Rightarrow V_1=2n-2-T \]

即我们求出反演后 Delaunay 三角形的期望数量即可，由于每个 Delaunay 三角形的外接圆唯一对应一个空圆，因此我们只要求出空圆的期望数量即可。

考虑什么图形在反演后会变成空圆，不难发现只有两种情况：

• 反演中心在空圆外。
• 反演中心在满圆内。

也就是说，我们求出所有原图形的空圆和满圆后，对矩形求面积交即可。

这里给出一种能一起求出所有空圆和满圆的算法。

将所有点作 \(f:(x,y)\rightarrow (x,y,x^2+y^2)\) 映射到三维空间中。

不难发现对于任意不与 \(z\) 轴平行且与抛物面 \(f\) 有交的平面 \(P\) ，将 \(P\) 在 \(f\) 上方的区域投影到平面 \(z=0\) 上，其图形为一个圆形，且所有平面上的圆与所有满足条件的平面形成双射。

并且所有不在圆内的点，那些点对应的点也在圆对应的平面上方。

因此我们求出映射后的点的三维凸包，每个上凸面对应一个原图的满圆，每个下凸面对应一个原图的空圆。

时间复杂度 \(O(n^2)\) 。