忘光了,所以复习【STR】
字符串
本文字符串下标从 \(1\) 开始。
\(S[l,r]\) 表示字符串 \(S\) 从 \(l\) 到 \(r\) 的部分。
速通
哈希
没什么可说的,我也不喜欢用。
trie
顾名思义,就是一个像字典一样的树。
基础
01trie
在一些题目中,可以用 trie 维护 01 串。
给定一棵 \(n\) 个点的带权树,求异或和最大的简单路径。
\(0\le n\le 10^5,0\le w<2^{31}\)。
solution
考虑树上两点路径的异或和可以转化为根到两点的异或和异或起来。
于是转化为求寻找两点使两点的权值的异或和最大。
用 trie 维护:不断插入一个数,查询这个数与已插入的数的最大异或和是多少(只要尽量保证前缀是 1)。
自动机
定义
自动机是一个对信号序列进行判定的数学模型。
比如说,你在初始状态,可以往几条路走,通过这几条路可以走到其他状态。
一个确定有限状态自动机(DFA,deterministic finite automation)由以下五部分构成:
(另外有个东西叫做 NFA,以后可能会提到)
- 字符集(\(\sum\)),该自动机只能输入这些字符。
- 状态集合(\(Q\)),顾名思义。
- 起始状态(\(st\)),同样顾名思义,\(st\in Q\)。
- 接受状态集合(\(F\)),\(F\subseteq Q\),或终止状态集合。
- 转移函数(\(\delta(x,y)\)),\(x\) 是一个状态,\(y\) 是字符串,意思就是从 \(x\) 开始,走一个字符串 \(y\) 。
以上的字符串均为广义的。
想要更快的理解,可以把 DFA 看做一个有向图,但是 DFA 只是一个数学模型。
另外不难发现 trie 也是自动机,我称其为广义前缀自动机。下面就拿 01trie 举个例子。
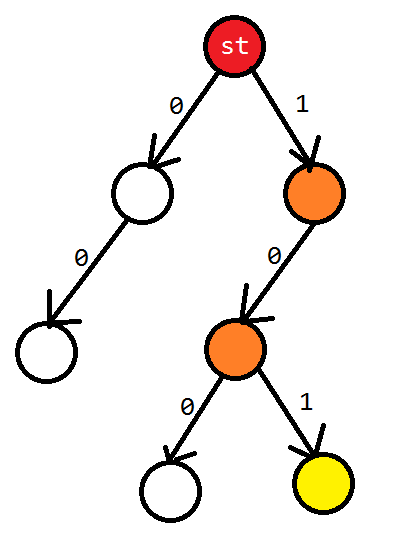
- \(\sum\):0/1。
- \(Q\):每个节点。
- \(st\):如图。
- \(F\):如图黄点。
- \(\delta\):\(\delta(st,101)\)。
边可以看做状态转移。
序列自动机
对于字符串 \(S\) 的一个子串 \(s\),\(\delta(st,s)\) 表示 \(s\) 在 \(S\) 中第一次出现时末位。
转移(\(u\) 是位置,\(c\) 是个字符):\(\delta(u,c)=\min(i|i>u,s_i=c)\)
可以通过记录下一个字符出现位置来实现。
给你两个由小写英文字母组成的串 \(A\) 和 \(B\),求:
- \(A\) 的一个最短的子串,它不是 \(B\) 的子序列。
- \(A\) 的一个最短的子序列,它不是 \(B\) 的子序列。
\(n\le2000\)
solution
第一个相对简单。直接枚举起点跑就行。
设 \(f_{i,j}\) 表示在 \(A\) 中到第 \(i\) 位,在 \(B\) 中到第 \(j\) 位的答案。
那么 \(f_{i,j}=\min\{f_{\delta(i,c),\delta(j,c)}+1\}\)
KMP
设 \(\mathrm p_i\) 表示前 \(i\) 位最长相同真前后缀长度。
对于字符串 \(\texttt{abbaabb}\)
- \(\mathrm p_1=0\):\(\texttt{a}\)
- \(\mathrm p_2=0\):\(\texttt{ab}\)
- \(\mathrm p_3=0\):\(\texttt{abb}\)
- \(\mathrm p_4=1\):\(\underline{\texttt{a}}\texttt{bb}\underline{\texttt{a}}\)
- \(\mathrm p_5=1\):\(\underline{\texttt{a}}\texttt{bba}\underline{\texttt{a}}\)
- \(\mathrm p_6=2\):\(\underline{\texttt{ab}}\texttt{ba}\underline{\texttt{ab}}\)
- \(\mathrm p_7=3\):\(\underline{\texttt{abb}}\texttt{a}\underline{\texttt{abb}}\)
处理出 \(\mathrm p_i\) 有什么用呢?
模式串在匹配文本串的时候,如果是以下这个状态:

发现到第五位时失配了,我们接下来肯定是想让它从蓝色这个状态继续匹配。
可以发现,跳到 \(\mathrm p_i\) 一定不劣。即比如在第五位失配了,就跳到 \(\mathrm p_4=1\) 位,如果跳到这里发现可以匹配下去,由于前后缀相同,所以可以继续匹配下去。如果不能匹配下去,那就继续往前跳。
由于每次只往后移动一格,往前跳的次数一定小于等于往后走的次数,复杂度 \(O(n)\)。
怎么求 \(\mathrm p\) 呢。
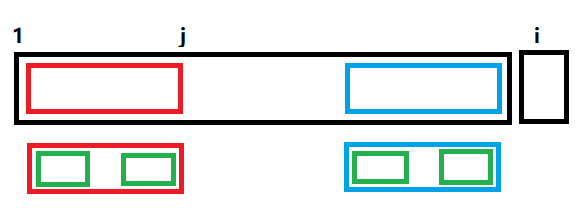
假设当前位是 \(i\),\(\mathrm p_{i-1}=j\)。如果 \(\mathrm p_i>\mathrm p_j\),那么 \(\mathrm p_i=\mathrm p_j+1\) 且 \(S_{j+1}=S_i\)。
否则,贪心地令 \(j=\mathrm p_j\),即上图绿框,可以发现如果此时 \(S_{j+1}=S_i\) 还是可以下去且最优。
最后,不难发现 kmp 的过程与求 \(\mathrm p\) 的过程类似,代码:
int j=0;
for(int i=2;i<=m;i++){
while(j&&b[i]!=b[j+1])j=pre[j];
j+=(b[i]==b[j+1]);pre[i]=j;
}
j=0;
for(int i=1;i<=n;i++){
while(j&&a[i]!=b[j+1])j=pre[j];
j+=(a[i]==b[j+1]);
if(j==m)write(i-m+1,'\n'),j=pre[j];
}
KMP自动机
用 KMP 建出的自动机,转移:
求有多少个 \(N\) 位数字文本串满足:没有一个子串为给定模式串。
模式串长度为 \(M\),对 \(K\) 取模。
\(N\leq10^9,M\leq20,K\leq1000\)
solution
dp,设 \(f_{i,j}\) 表示文本串中匹配到第 \(i\) 位,模式串中匹配到第 \(j\) 位的方案数。
那么:
\[\begin{aligned} f_{i,j}=&\sum _c\sum_{k,\delta(k,c)=j}f_{i-1,k}\\ =&\sum_{k}f_{i-1,k}\sum _c[\delta(k,c)=j]\\ \end{aligned} \]设矩阵 \(g\) 有: \(\displaystyle g_{k,j}=\sum _c[\delta(k,c)=j]\),就可以把转移看做向量乘上矩阵。
又发现 \(g\) 与 \(i\) 无关,于是矩阵快速幂。
失配树
border
任意长度相同前后缀。
失配树
考虑一个问题:
给定 \(S\),\(T\) 次询问 \(p,q\),求 \(p\) 前缀和 \(q\) 前缀的最长公共 border。
首先,根据 KMP 中 \(\mathrm p_i\) 的定义,从一个点开始不断往上跳 \(\mathrm p_i\),跳到的就是它的所有 border。
而仔细思考后发现一个点向它的 \(\mathrm p_i\) 连边,连出来的就是一个树形结构,我们称其为失配树。
而两段前缀的最长公共 border 转化为了失配树上的 LCA。
求出对于 \(S\) 每个前缀的不相交 border 个数。
对于一个前缀 \(S[1,i]\) 求不相交 border 可以转化为长度 \(\le \frac{i}2\),所以我们就可以在失配树上往上跳,跳到符合条件,深度就是答案。
可以不用显式建树。
Z 函数
令 \(\mathrm z_i\) 表示一个字符串 \(s\) 和 \(s[i,n]\) 的 LCP,特别的,\(\mathrm z_1=0\)。
对于字符串 \(\texttt{aaabaab}\)
- \(\mathrm z_1=0\):
- \(\mathrm z_2=2\):\(\underline {\texttt{a}\underline{\texttt{a}}}\underline{\texttt{a}}\)
- \(\mathrm z_3=1\):\(\underline {\texttt{a}}\texttt{a}\underline{\texttt{a}}\)
- \(\mathrm z_4=0\):
- \(\mathrm z_5=2\):\(\underline{\texttt{aa}}\texttt{ab}\underline{\texttt{aa}}\)
- \(\mathrm z_6=1\):\(\underline{\texttt{a}}\texttt{aaba}\underline{\texttt{a}}\)
- \(\mathrm z_7=0\):
Z 函数其实也很好求:
从某个位置 \(i\) 开始,与整串前缀相同的前缀(称为 Z-box)为 \(s[i,i+\mathrm z_i-1]\)。
我们维护当前 \(i+\mathrm z_i-1\) 的最大值 \(r\),以及其对应的 \(i\) ,令其为 \(l\)。
假设我们已经求出 \(1\sim i-1\) 的 Z 函数,接下来要求 \(\mathrm z_i\)。
根据定义,有 \(s[i,r]=s[i-l,r-l]\),所以,\(\mathrm z_i\ge\min({\mathrm z_{i-l}},r-i+1)\)。
如果还有机会继续拓展(\(r-i+1\le \mathrm z_{i-l}\)),那就右移 \(r\),否则就 G 了。
l=1,r=0;
for(int i=2;i<=m;i++){
if(i<r)z[i]=min(z[i-l+1],r-i+1);
while(i+z[i]<=m&&b[i+z[i]]==b[z[i]+1])++z[i];
if(i+z[i]-1>=r)r=i+z[i]-1,l=i;
}
匹配另一个串
拼起来再做一遍即可。
但是注意拼起来时中间放一个随便什么引荐字符,避免匹配到后面的串。
给字符串 \(S\),求 \(S = {(AB)}^iC\) 的方案数,设 \(F(S)\) 表示 \(S\) 中出现奇数次的字符数量,有 \(F(A)\le F(C)\)。定义乘法为前后拼接。
solution
枚举循环节长度:
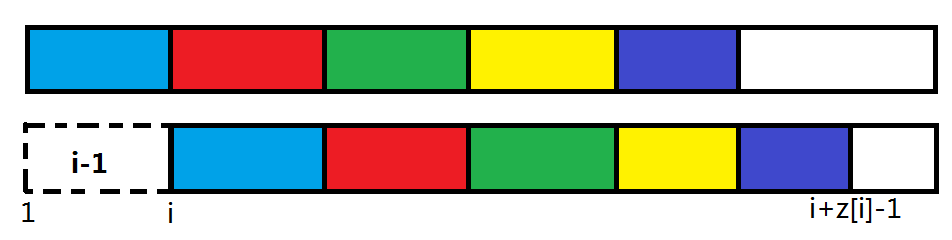
如图为长度为 \(i-1\) 的循环节,不难发现有颜色的段是完全相同的,而且不能再往后延伸一段。
可以得出,最大循环节段数为 \(t_i=\displaystyle\left\lfloor\frac{\mathrm z_i}{i-1}\right\rfloor+1\)。注意:为了最后留至少一个字符给 \(C\),所以如果循环节把整串排满了,要 \(-1\)。
设 \(pre_i\) 表示 \(S[1,i]\) 中出现奇数次的字符数量,\(suf_i\) 表示 \(S[i,n]\) 中出现奇数次的字符数量。
对循环节段数 \(k\) 奇偶分类讨论:
\(k\equiv1\pmod 2\)
不难发现,段数为奇数时,\(F(C)\) 保持不变(两个不同的奇数 \(k\) 对应的串 \(C\) 只差偶数段循环节,正好抵消了)。
所以,我们只要找到 \(S[1,j](j<i)\) 使得 \(F(A)=pre_j\le F(C)=suf_i\)(算 \(k=1\) 时的 \(F(C)\))。
这部分的贡献为:满足条件的 \(j\) 的个数 \(\times\) 满足条件的 \(k\) 的个数。
\(k\equiv0\pmod 2\)
段数为偶数时 \(F(C)\) 也保持不变(原因同上),且等于 \(suf_1\)。
所以,我们只要找到 \(S[1,j](j<i)\) 使得 \(F(A)=pre_j\le F(C)=suf_1\)。
这部分的贡献为:满足条件的 \(j\) 的个数 \(\times\) 满足条件的 \(k\) 的个数。
然后发现做完了。
🐴拉🚗
求 \(S\) 中最长回文串长度。
先把字符串变成 \(s_1|s_2|s_3|s_4|s_5\) 这个样子,这样一定有一个中心。
模仿 Z 函数,设 \(\operatorname{manacher}_i\) 表示以 \(i\) 为中心最长回文串半边长(包括中间)。
我们维护当前 \(i+\operatorname{manacher}_i-1\) 的最大值 \(r\),以及其对应的 \(i\) ,令其为 \(mid\)。
可以考虑把 \(i\) 以 \(mid\) 为中心翻折,得到 \(\operatorname{manacher}_i\ge\min(\operatorname{manacher}_{2mid-i},r-i+1)\)。
然后跟 Z 函数类似地右移 \(r\) 即可。
int mid=0,r=0;
for(int i=1;i<n;i++){
if(i<=r)manacher[i]=min(manacher[(mid<<1)-i],r-i+1);
while(s[i-manacher[i]]==s[i+manacher[i]])++manacher[i];
if(manacher[i]+i-1>=r)r=manacher[i]+i-1,mid=i;
}
AC 自动机
多模式串 \(s_i\) 配单文本串 \(S\)。
先将模式串 \(s_i\) 都放到 trie 里面。
记 \(\operatorname{fail}_i\) 表示 trie 上的一个点 \(i\) 的最长能在 trie 上查询的真后缀的对应节点。
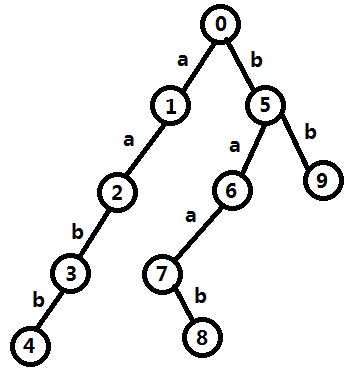
- \(\operatorname{fail}_1=0\):最长真后缀为 \(\varnothing\)
- \(\operatorname{fail}_2=1\):最长真后缀为 \(\texttt{a}\)
- \(\operatorname{fail}_3=5\):最长真后缀为 \(\texttt{b}\)
- \(\operatorname{fail}_4=9\):最长真后缀为 \(\texttt{bb}\)
- \(\operatorname{fail}_5=0\):最长真后缀为 \(\varnothing\)
- \(\operatorname{fail}_6=1\):最长真后缀为 \(\texttt{a}\)
- \(\operatorname{fail}_7=2\):最长真后缀为 \(\texttt{aa}\)
- \(\operatorname{fail}_8=3\):最长真后缀为 \(\texttt{aab}\)
- \(\operatorname{fail}_9=5\):最长真后缀为 \(\texttt{b}\)
构建方法:设当前求 \(i\) 点的 \(\operatorname{fail}\),那就从 \(i\) 在 trie 上的父亲 \(fa_i\) 开始,往上跳 \(\operatorname{fail}\) 直到可以往下走为止。
具体的,设当前在点 \(u\) :
- 若 \(\operatorname{trie}_{u,c}\) 存在,那么 \(\operatorname{fail}_{\operatorname{trie}_{u,c}}=\operatorname{trie}_{\operatorname{fail}_u,c}\)
- 否则,令 \(\operatorname{trie}_{u,c}=\operatorname{trie}_{\operatorname{fail}_u,c}\)
inline void init(){
L=1,R=0;
for(int i=0;i<26;i++)
if(trie[0][i])q[++R]=trie[0][i];
while(L<=R){
int u=q[L++],t=fail[u];
for(int i=0;i<26;i++){
int v=trie[u][i];
if(v)fail[v]=trie[t][i],q[++R]=v;
else trie[u][i]=trie[t][i];
}
}
}
第二个操作可以使不断往上跳 \(\operatorname{fail}\) 的过程一步到位。
匹配方法:如果文本串在树上匹配到了一个串,那么一定能匹配到跳 \(\operatorname{fail}\) 能跳到的所有点。
给定 \(n\) 个模式串 \(s_i\) 和一个文本串 \(t\),求有多少个不同的模式串在文本串里出现过。
\(1 \leq |t| \leq 10^6\),\(1 \leq \sum\limits_{} |s_i| \leq 10^6\)。
如果一个串出现过了,那么它的所有 \(\operatorname{fail}\) 都出现过,所以我们只要在节点上打个 tag,如果访问过了,就不继续。
复杂度 \(O(|t|+26\sum|s_i|)\)。
fail 树
不难发现,AC 自动机的 \(\operatorname{fail}\) 和 KMP 的 \(\operatorname{p}\) 一样可以连成一棵树。
有 \(N\) 个由小写字母组成的模式串 \(s_i\) 以及一个文本串 \(T\)。你需要找出哪些模式串在文本串 \(T\) 中出现的次数最多。
\(N\le150,|s_i|\le70,|T|\le10^6\)
这题暴力可过,但是同样可以在 fail 树上树形 dp。
【模板】AC 自动机(二次加强版) 要树形 dp 才能过。
复杂度 \(O(|t|+26\sum|s_i|)\)。
非速通
SAM
一个字符串 \(S\) 的 SAM 是一个接受 \(S\) 的所有后缀的最小 DFA。
从初始状态出发,转移到了一个终止状态,则路径上所有转移连起来一定是 \(S\) 的一个后缀。
\(S\) 的每个子串均可用一条从初始状态到某个状态的路径构成。
结束位置(endpos)
对于 \(S\) 的一个非空子串 \(s\),记 \(\operatorname{endpos}(s)\) 为 \(S\) 中所有 \(s\) 的结束位置集合,令 \(\operatorname{endpos}(st)=\{x|x\in\mathbb{N},x\le |S|\}\)(注意包含 \(0\))。
对于字符串 \(\texttt{abababbb}\),\(\operatorname{endpos}(\texttt{ab})=\{2,4,6\}\)。
可能存在两个 \(S\) 的非空子串 \(s_1,s_2\),满足 \(\operatorname {endpos}(s1)=\operatorname {endpos}(s2)\),这样所有 \(S\) 的非空子串可以依据 \(\operatorname {endpos}\) 分为若干个等价类。
SAM 中的每个状态对应一个或多个 \(\operatorname {endpos}\) 相同的子串。
所以 SAM 中的状态数等于所有子串的等价类的个数,再加上初始状态。
由 \(\operatorname {endpos}\) 我们可以得到一些重要结论:
-
字符串 \(S\) 的两个不同非空子串的 \(\operatorname {endpos}\) 相同,当且仅当其中一个每一次出现都是以另一个的真后缀的形式存在的。
证明:如果 \(\operatorname {endpos}\) 相同,所以较短者必为较长者的真后缀,所以在较长者每一次出现时,较短者必出现。
-
对于字符串 \(S\) 的两个非空子串 \(s_1,s_2\)(\(|s_1|\le|s_2|\)),有 \(\operatorname {endpos}(s_1)\subseteq\operatorname {endpos}(s_2)\),或 \(\operatorname {endpos}(s_1)\cap\operatorname {endpos}(s_2)=\varnothing\)。取决于 \(s_1\) 是否为 \(s_2\) 的后缀。
证明:如果 \(\operatorname {endpos}(s_1)\cap\operatorname {endpos}(s_2)\neq\varnothing\),那么在一个位置定有 \(s_1\) 以 \(s_2\) 的后缀的形式出现,那么在每次 \(s_2\) 出现时 \(s_1\) 必以其后缀形式出现,即 \(\operatorname {endpos}(s_1)\subseteq\operatorname {endpos}(s_2)\)。
-
一个 \(\operatorname {endpos}\) 等价类中的所有子串长度恰好覆盖一个区间。
证明:
令等价类中长度最小的字符串为 \(s_l\),最大的为 \(s_r\),那么 \(s_l\) 是 \(s_r\) 的后缀。
对于 \(s_r\) 一个后缀 \(s(|s|\ge|s_l|)\),由第二个结论:\(\operatorname {endpos}(s_l)\subseteq\operatorname {endpos}(s),\operatorname {endpos}(s)\subseteq\operatorname {endpos}(s_r)\)。
又有 \(\operatorname {endpos}(s_l)=\operatorname {endpos}(s_r)\),所以 \(\operatorname {endpos}(s_l)=\operatorname {endpos}(s_r)=\operatorname {endpos}(s)\)
即满足条件的 \(s\) 均会出现在等价类中,所以恰好覆盖一个区间。
后缀链接 (link)
令 \(\operatorname {endpos}(x)\) 等价类中长度最大的为 \(t_x\)。
一个后缀链接 \(\operatorname{link}(x)\) 中, \(x\) 代表一个状态,设 \(t_x\) 后缀中最长且不属于 \(\operatorname {endpos}(x)\) 的后缀为 \(g\),那么 \(\operatorname{link}(x)\) 指向 \(g\) 所在的状态。
不难发现,\(\operatorname{link}\) 也能类似于 \(\operatorname{fail}\) 变成一棵以 \(st\) 为根的树,我们叫它后缀链接树或 parent 树。
一些性质(对于一个字符串 \(S\)):
-
共有 \(|S|\) 个叶子结点,代表 \(S\) 的 \(|S|\) 个前缀所属状态。
证明:没有点会链接到前缀对应的等价类,非前缀不是属于前缀所在状态,就是能通过 link 。
-
后缀链接树(SAM)的节点个数最多为 \(2n-1\),后面会证。
-
任意串的后缀全部位于该串所在状态的后缀链接路径上。
-
一个状态的 \(\operatorname{endpos}\) 是后缀链接树上子树内所有叶子的 \(\operatorname{endpos}\) 的并。
后缀链接树上的边可以看做 \(\operatorname{endpos}\) 的偏序关系。
线性构造
后缀链接树不够用,建出 SAM 才行。(建 SAM 的算法叫 Blumer 算法)
令 \(\operatorname {endpos}(x)\) 等价类中长度最大的长度为 \(\operatorname{len}(x)\)。
假设当前已经完成了 \([1,i-1]\) 的,当前加入字符 \(S_i=c\)。
- 设 \([1,i-1]\) 这一前缀所在状态是 \(last\),那我们创建一个新节点 \(u\),表示后缀 \([1,i]\) 所在状态,由定义:\(\operatorname{len}(u)=\operatorname{len}(last)+1\)。
- 从 \(last\) 开始跳 \(\operatorname{link}\),如果当前状态没有 \(c\) 的转移,那就创建一个 \(c\) 的转移,指向 \(u\)。
- 如果跳到了有 \(c\) 的转移的点,设其为 \(p\),设 \(q\) 为 \(\delta(p,c)\),如果 \(\operatorname{len}(q)=\operatorname{len}(p)+1\),那就令 \(\operatorname{link}(u)=q\)。
- 否则,构造一个新点 \(v\),\(v\) 继承 \(q\) 出发的转移和 \(\operatorname{link}\),并且 \(\operatorname{len}(v)=\operatorname{len}(p)+1\),然后令 \(\operatorname{link}(u)=\operatorname{link}(q)=v\)。
- 最后,要从 \(p\) 继续跳 \(\operatorname{link}\),并把路径上原来指向 \(q\) 的边指向 \(v\)。
复杂度证明:
不难发现,一次加点最多加两个,再加上前两个点不可能加点,一共 \(2n-2\),但是还有初始状态,所以是 \(2n-1\) 个。
发现转移数也是 \(3n+O(1)\) 的,具体可以看 这里。
其它部分的复杂度显然,主要是两次跳 \(\operatorname{link}\) 的过程。
第一次比较显然,最多创建转移数条新边。
对于第二次:
不难发现,第二次跳 \(\operatorname{link}\) 的过程跳到第一个不指向 \(q\) 的位置就可以停了,再往上跳,就会指向 \(\operatorname{link}(q)\)。
设 \(\text{depth}(x)\) 表示后缀链接树上 \(x\) 的深度。
- 引理:若 \(x\to y\) 存在转移边,则 \(\text{depth}(x)+1\ge\text{depth}(y)\)。
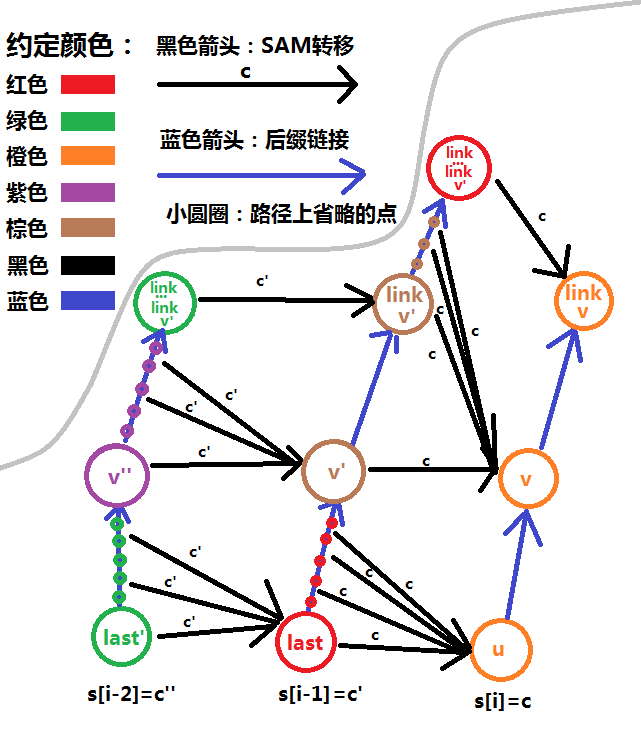
\(last'\) 表示在构建 \(last\) 时的 \(last\),\(v\) 在一些时候可能代表 \(q\)。
在构建 \(last\) 时,第一次跳 \(\operatorname{link}\) 的过程为下面的绿色部分,第二次为紫色部分,令紫色部分最上方的点为 \(t''\)。
构建 \(u\) 时,第一次跳 \(\operatorname{link}\) 的过程为下面的红色部分,第二次为棕色部分,令棕色部分最上方的点为 \(t'\)。
不难发现,构建 \(last\) 时第二次跳的距离为 \(\text{depth}(v'')-\text{depth}(t'')+1\),构建 \(u\) 时为 \(\text{depth}(v')-\text{depth}(t')+1\)。
引理 \(\text{depth}(v')\le\text{depth}(t'')+1\),换句话说就是 \(t''\) 最多往一层。
这说明,构建一个点时第二次开始跳的位置的深度,最多是构建上一个点时第二次结束的位置的深度 \(+1\)。
不难发现深度最多 \(+|S|\),构建而跳一直是跳到深度更低的,所以势能分析一下,复杂度 \(O(|S|)\)。
瓶颈在于复制。
朴素的构造是 \(O(|\sum||S|)\)(每次复制时 memcpy)或 \(O(|S|\log|\sum|)\)(使用 std::map)的。
当然也可以开一个 std::vector,在每次加转移时把字符压进去。这样可以均摊 \(O(n)\) 复制。
但是由于常数问题,\(|\sum|=26\) 时第一种最快。
代码:
inline void add(int c){
int p=last,u=++cnt;last=u;
clear(u);len[u]=len[p]+1;
while(p&&!son[p][c])son[p][c]=u,p=link[p];
if(!p){link[u]=1;return;}
int q=son[p][c];
if(len[q]==len[p]+1){link[u]=q;return;}
int v=++cnt;copy(v,q);len[v]=len[p]+1;link[u]=link[q]=v;
while(p&&son[p][c]==q)son[p][c]=v,p=link[p];
}
本文字符串下标从 \(1\) 开始。
\(S[l,r]\) 表示字符串 \(S\) 从 \(l\) 到 \(r\) 的部分。
应用
检查字符串是否出现
给定 \(n\) 个模式串 \(s_i\) 和一个文本串 \(t\),求有多少个不同的模式串在文本串里出现过。
\(1≤|t|≤10^6\),\(1≤∑|s_i|≤10^6\)。
直接根据建出来的 SAM 转移即可。
计算字符串出现次数
显然,一个字符串 \(s\) 在 \(S\) 中的出现次数为 \(\displaystyle \sum_{i=1}^{|S|}[s\text{ is a suffix of }S[1,i]]\)。
而如果 \(s\) 是一个 \(S[1,i]\) 的后缀,那么在后缀链接树上 \(s\) 对应的节点定是 \(S[1,i]\) 对应的叶子结点的祖先。
于是树形 dp 即可。
有 N 个由小写字母组成的模式串 si 以及一个文本串 S,求每个模式串在文本串中的出现次数。
\(1≤n≤2×10^5\),\(∑|s_i|≤2×10^5\), \(|S|≤2×10^6\)。
上面已经讲了,但是被卡空间了。【模板】后缀自动机 (SAM) 也类似。
本质不同的子串个数
一个子串就是一条从 \(st\) 开始的路径,而 SAM 又是一张 DAG,所以转换为求 DAG 上本质不同路径条数,可以拓扑排序+DP,转移方程 \(d_u\) 表示点 \(u\) 的出度:
但是有更优美的做法,每个状态对应的 \(\operatorname{endpos}\) 等价类中的元素,与从 \(st\) 开始、以该状态结尾的路径构成双射。
所以只需求出每个点的等价类大小,即对于点 \(x\),\(\operatorname{len}(x)-\operatorname{len}(\operatorname{link}(x))\)。
给一个的字符串,求不同的子串的个数。
直接来即可。
共进行 \(n\) 次操作,每次在数组 \(S\) 的末尾加入一个数 \(x_i\)。每次操作求出,\(S\) 的不同子串个数。
\(n\le10^5,x_i\le10^9\)。
由于 \(x_i\) 比较大,用
std::map即可。每次末尾加一个数,注意一下即可。
本质不同子串总长度
拓扑排序的方法同样行得通,转移方程(\(f_u\) 是上一题的):
第二种同样行得通,因为 \(\operatorname{endpos}\) 等价类恰好形成一个区间,所以等差数列求和即可。
求字典序第 k 大子串
求出 \(f_i\) 之后,每一层减下去即可。
给定的长度为 \(n\) 的字符串,求出它的第 \(k\) 小子串是什么。
\(t\) 为 \(0\) 则表示不同位置的相同子串算作一个,\(t\) 为 \(1\) 则表示不同位置的相同子串算作多个。
\(1\leq n \leq 5 \times 10^5\),\(0\leq t \leq 1\),\(1\leq k \leq 10^9\)。
\(t=1\) 时 \(f_i\) 还需改动一下。
求第一次出现的位置
维护 \(\operatorname{firstpos}(i)\) 表示该状态对应的 \(\operatorname{endpos}\) 等价类的第一次出现的末尾位置。
当加入新点时 \(\operatorname{firstpos}(u)=\operatorname{len}(u)\)。
复制一个点时 \(\operatorname{firstpos}(v)=\operatorname{firstpos}(q)\)。
第一次出现位置即为查询的字符串对应状态的 \(\operatorname{firstpos}\) 减去查询的字符串的长度再 \(+1\)。
求每一次出现的位置
每一次出现位置对应这后缀链接树上子树内所有叶子节点的位置。
暴力就可以了。