李超线段树

前言

本文主要介绍关于李超线段树的实现及具体应用，扩展，对其原理不做过多介绍。

在下文中，你可以认为 一次函数，等差数列，线段 是同一个东西。

引入与概括

思考下列问题：

在平面直角坐标系中维护一次函数的集合，支持以下两种操作：

• 加入一个定义域为 \([l,r]\) 的一次函数 \(y=kx+b\)。

• 查询所有定义域包含 \(x\) 的一次函数的函数值的最值。

我们发现，这个问题等价于维护一个序列 \(a\)，支持区间对等差数列取 \(\max\)，查询单点值。

具体的说，我们将一个一次函数 \(y=kx+b\,(x\in[l,r])\) 视为一个首项为 \(lk+b\)，公差为 \(k\) 的等差数列 \(b\)，那么这个操作相当于对于 \(i\in[l,r]\)，令 \(a_i\gets\max(a_i,b_i)\)。

我们要介绍的李超线段树就是用来解决这个问题的。

先介绍一下李超线段树的性质：

李超线段树是一种线段树的变体，是一种值域线段树，支持一些普通线段树难以实现的操作，比如区间对等差数列取 \(\max\) 或 \(\min\) 等。

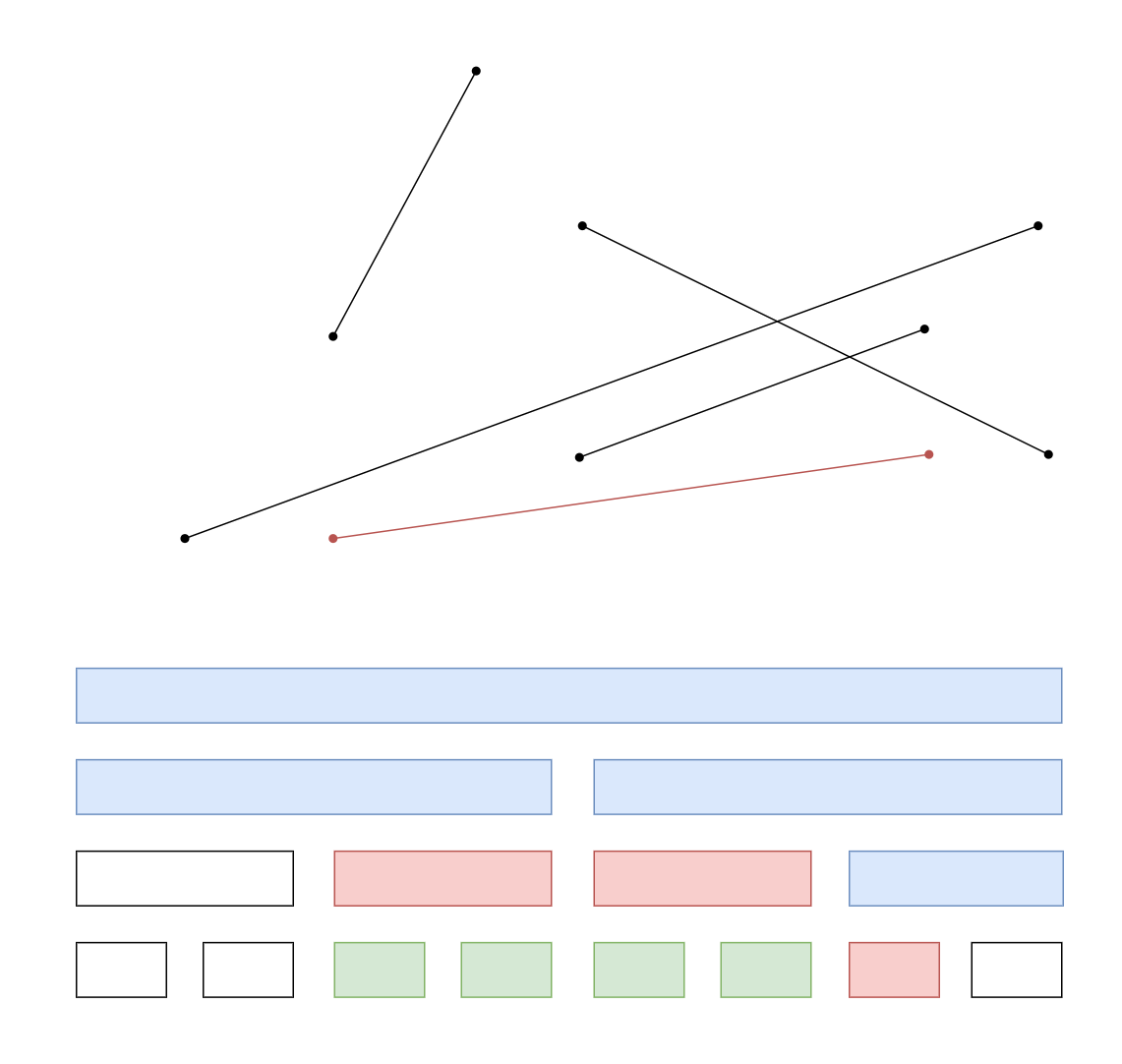
实现与分析

我们在线段树的每一个节点维护当前区间可能成为最优解的线段（一次函数，等差数列），即该线段在区间的某个下标上有最优解。

• 前置处理（以维护最小值为例）

struct Line{//每一条直线用斜截式 k,b 表示
	int k, b;
}line[N];

int calc(int id, int x){//对应给定线段和横坐标计算纵坐标
	return x * line[id].k + line[id].b;
}

bool Less(int id1, int id2, int x){//比较线段的函数值的优劣
	return calc(id1, x) < calc(id2, x);
}

• 插入

插入直线：

void add(int p, int l, int r, int id){
    if (!a[p]) {a[p] = id; return ;}
	if (l == r) {if(Less(id, a[p], l)) a[p] = id; return ;}
	if (Less(id, a[p], mid)) swap(a[p], id);
	if (Less(id, a[p], l)) add(ls, l, mid, id);
	if (Less(id, a[p], r)) add(rs, mid + 1, r, id);
}

插入线段：

void add(int p, int l, int r, int x, int y, int id){//先找到线段对应的区间再按直线的方式插入
	if (x <= l && r <= y) {
		if (!a[p]) {a[p] = id; return ;}
		if (l == r) { if(Less(id, a[p], l)) a[p] = id; return ;}
		if (Less(id, a[p], mid)) swap(a[p], id);
		if (Less(id, a[p], l)) add(ls, l, mid, x, y, id);
		if (Less(id, a[p], r)) add(rs, mid+1, r, x, y, id);
		return ;
	}
	if (x <= mid) add(ls, l, mid, x, y, id);
	if (y > mid) add(rs, mid + 1, r, x, y, id);
}

• 查询

查询函数值：

int query(int p, int l, int r, int x){
    if (!a[p]) return inf;
    int res = calc(a[p], x);
	if (l == r) return res;
	if (x <= mid) res = min(res, query(ls, l, mid, x));
	else res = min(res, query(rs, mid + 1, r, x));
	return res;
}

查询函数值对应线段：

int query(int p, int l, int r, int x){
	if (l == r) return a[p];
    int res = 0;
	if (x <= mid) res = query(ls, l, mid, x);
	else res = query(rs, mid + 1, r, x);
    return Less(a[p], res, x) ? a[p] : res;
}

时间复杂度：

单次查询的时间复杂度为 \(O(\log n)\)。

插入直线的时间复杂度为 \(O(\log n)\)。

插入线段的时间复杂度为 \(O(\log^2n)\)。

应用与扩展

李超线段树主要用于斜率优化，而在斜率优化中通常只需要套板子即可。

李超线段树的拓展包括：

李超线段树优化最短路

李超线段树合并优化 DP

李超线段树套树剖