凸包

定义及性质

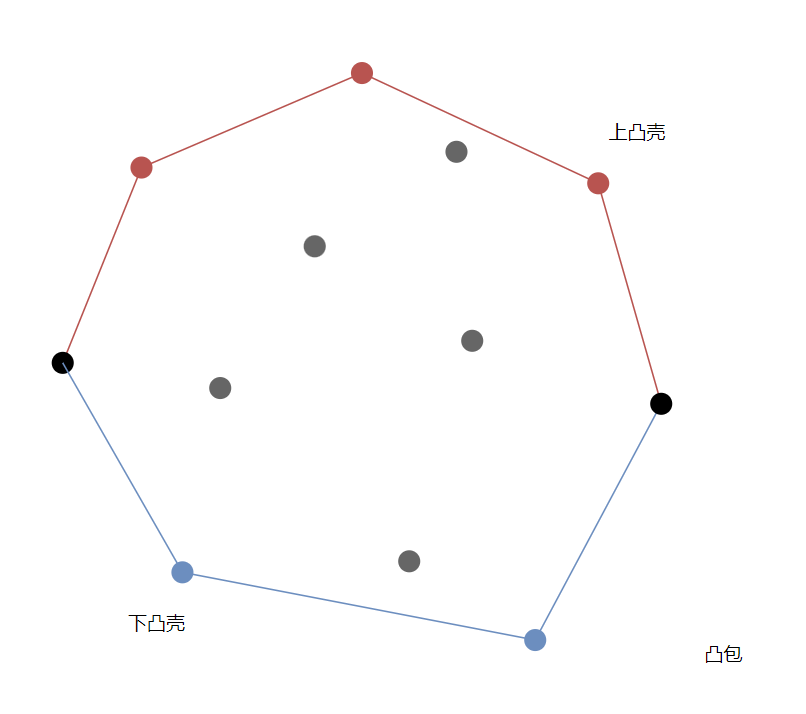
能够覆盖平面上所有给定点的最小凸多边形叫做凸包，也叫凸壳。

我们按照斜率的正负性将凸壳划分为两种：斜率均为正的是上凸壳，斜率均为负的是下凸壳。

容易发现，在上凸壳上的直线斜率单调下降，在下凸壳上的直线的斜率单调上升。

凸包是所有能覆盖所有点的凸多边形中面积和周长最小的。

求法及作用

凸包的常用求法是 Andrew 算法，其过程如下：

1. 将所有点按横坐标升序排序。

2. 从第一个点开始，维护一个单调栈。

3. 逐一尝试加入点，如果新点与栈顶的点构成的直线的斜率小于栈顶的点与栈顶上一个点构成的直线的斜率，那么重复弹出栈顶直到不小于为止，再将该点入栈。

4. 重复 3 过程直到所有点被尝试过，这时所有还在栈内的点构成了下凸壳。

5. 按照类似的过程再求一遍上凸壳，拼接起来就是整个凸包。

struct Point{
	int x,y;
}a[N];
int hh,tt,q[N];

double slope(int i,int j){
	return 1.0*(a[i].y-a[j].y)/(a[i].x-a[j].x);
}

void Andrew_Lowerconvexshell(){//只求出了下凸壳，上凸壳同理
	hh=1,tt=0;
	sort(a+1,a+n+1,[](Point a,Point b){return a.x<b.x;});
	for(int i=1;i<=n;i++){
		while(hh<=tt&&slope(i,q[tt])<slope(q[tt],q[tt-1])) tt--;
		q[++tt]=i;
	}
}

该算法的时间复杂度是 \(O(n\log n)\)，瓶颈在于排序。这是因为在单调栈过程中，每一个点至多被加入弹出一次。

也就是说，如果已经保证了所有点横坐标单调，那么求凸包的时间复杂度是 \(O(n)\) 的。

凸包常用于 DP 的优化，DP 方程的凸性是一个重要的性质。

可以使用平衡树（splay，FHQTreap，set 等）来维护动态凸包，支持动态插入（离线删除）。