【Leetcode】935. 骑士拨号器——1690

题目

📝 题目描述

象棋骑士有一个独特的移动方式，它可以垂直移动两个方格，水平移动一个方格，或者水平移动两个方格，垂直移动一个方格(两者都形成一个 **L **的形状)。

象棋骑士可能的移动方式如下图所示:

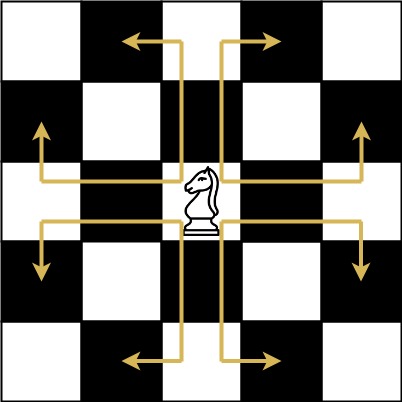
我们有一个象棋骑士和一个电话垫，如下所示，骑士只能站在一个数字单元格上(即蓝色单元格)。

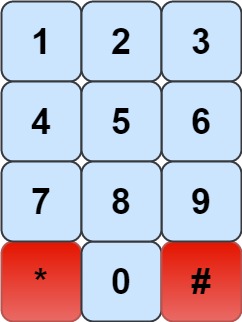
给定一个整数 n，返回我们可以拨多少个长度为 n 的不同电话号码。

你可以将骑士放置在任何数字单元格上，然后你应该执行 n - 1 次移动来获得长度为 n 的号码。所有的跳跃应该是有效的骑士跳跃。

因为答案可能很大，**所以输出答案模 **109 + 7.

提示：

• 1 <= n <= 5000

🔍思路

通过题目讲解的象棋骑士的移动方式，可以发现实际上就是中国象棋的马走日。

而对于从0~10的每个位置，其能够去到的位置是固定的。可以提前确定的。

例如 0 只能去 4 、6； 5 没有地方可以去

题目要求给出n次移动后得到的电话号码长度，实际上也就是n次移动可能的所有路径。

对于第n次移动，其只与n-1次移动到达的位置有关。因此考虑使用DP

\(dp[i][j]=sum(dp[i-1][k]\ for\ k\ in\ step[j])\)

启动dp[i][j]表示第i次移动到达j位置可能的路径条数；step[j]表示由位置j可以到达的位置集合。

考虑到实际上dp[i]只与dp[i-1]相关，因此可以使用一维的变量以减少空间复杂度。

✍️ 代码实现

在代码具体实现中，可以提前预处理所有的结果，调用的时候直接返回结果即可。减少由于多次重复计算导致的时间浪费。

step = [[4, 6], [6, 8], [7, 9], [4, 8], [0, 3, 9], ], [0, 1, 7], [2, 6], [1, 3], [2, 4]]

dp = [10]
t = [1] * 10
for i in range(5000):
    t = [sum(t[j] for j in step[i])% (10**9 + 7) for i in range(10)]
    dp.append(sum(t) % (10**9 + 7))

class Solution:
    def knightDialer(self, n: int) -> int:
        return dp[n-1]