题解：[TJOI2015] 概率论

题目传送门

题意分析

首先，对于这种输入只有一个数，从这一个数就能推出答案的题目，大概率是个毒瘤数学题。如此考虑求解。

求期望，期望即总叶节点数除以不同构的二叉树个数。

令 \(n\) 个节点的不同构二叉树个数为 \(f_n\)，其叶节点总数为 \(g_n\)，则答案即 \(\dfrac{g_n}{f_n}\)。

考虑如何求解 \(f_n,g_n\)。

先考虑求解 \(f_n\)。其实 \(f_n\) 的求解是较为简单的，因为二叉树具有一个性质：根节点的左右子节点的子树仍然是二叉树。

令左子树的大小为 \(k\)，则右子树的大小为 \(n-k-1\)，总数 \(f_n\) 即左子树与右子树组合得到的结果：

\[f_n=\sum_{k=0}^{n-1}f_kf_{n-k-1} \]

可以发现，此即 Catalan 数。

由 Catalan 数通项公式（只需要使用生成函数+牛顿二项式定理即可解得），可得：

\[f_n=\dfrac{1}{2n+1}\dbinom{2n}{n} \]

---

现在考虑求解 \(g_n\)。

二叉树具有一个性质：如果给大小为 \(n-1\) 的二叉树每一个最外层的节点补满左右子节点，则添加的节点数为 \(n\)。

考虑数学归纳法。

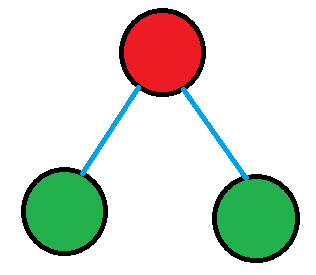
当 \(n=2\) 时，添加的 \(2\) 个节点即根节点的左右子节点，命题成立。

假设 \(n=k\) 时命题成立。

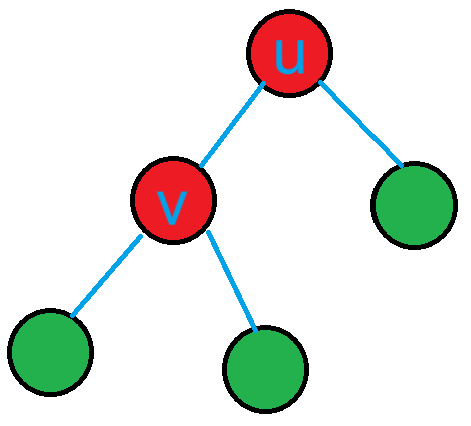
当 \(n=k+1\) 时，可视为在某个 \(k\) 个节点的树上添加了一个节点得到；设添加节点为 \(v\)，其父节点为 \(u\)。

\(u\) 原本可以添加 \(2\) 个节点，现在因为有了子节点 \(v\)，因此对答案的贡献减少了 \(1\)。但是 \(v\) 对答案有大小为 \(2\) 的贡献，因此 \(n=k+1\) 时的答案为 \(n=k\) 时的答案加 \(1\)，即 \(k+1=n\)。

故，原命题成立。

那么就可以枚举这个添加的节点，在每一棵树上对于答案的贡献均为 \(1\)，单个节点的总贡献为 \(f_{n-1}\)，共计 \(n\) 的节点的总贡献即 \(n\cdot f_{n-1}\)。

故，有：

\[g_n=n\cdot f_{n-1}=\dfrac{n}{2n-1}\dbinom{2n-2}{n-1} \]

---

答案即：

\[\begin{aligned} \dfrac{g_n}{f_n}&=\dfrac{\dfrac{n}{2n-1}\dbinom{2n-2}{n-1}}{\dfrac{1}{2n+1}\dbinom{2n}{2n}}\\ &=\dfrac{n(n+1)}{2(2n-1)} \end{aligned} \]

AC 代码

//#include<bits/stdc++.h>
#include<algorithm> 
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
int n;
long double f(long long n){
	return n*(n+1)*1.0/(4*n-2);
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	
	cin>>n;
	cout.precision(9);
	cout.setf(ios::fixed);
	cout<<f(n)<<'\n';
	
	cout.flush(); 
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}