题解：叶子的染色

题目传送门

题意分析

注意

无色节点不是白色节点。

给定一棵 \(m\) 个节点的无根树并指定 \(n\) 个叶子节点。

规定根节点到叶子节点 \(i\) 的路径上深度最大的有色节点的颜色为 \(c_i\)，保证根节点的度数大于 \(1\)。

求最少染色节点数。

树型 DP

状态设计

暂不考虑因为根节点不同而产生的影响，后文会证明根节点的不同对答案没有影响。

设计 \(dp_{x,i}\)（\(i\in\{0,1\}\)）表示节点 \(x\) 染成颜色 \(i\) 时其子树内的最少染色节点数量。

首先，节点 \(x\) 不会不染色，因为染上一个颜色后不会比不染色更劣——可以将子节点的颜色染到自己身上，总染色节点数不变，且仍然满足要求。

那么，初始值显然就是所有的 \(dp_{x,i}=1\)，即其本身染色了。

对于叶子节点 \(x\)，显然不能够染成 \(c_x\) 之外的颜色，因此需要特判或者赋特殊值。我们可以将 \(dp_{x,1-c_x}\) 标记为一个极大值，来代表不能染成 \(1-c_x\)。（\(1-c_x\) 和 ![c[x]] 效果一样）

状态转移

这就简单了。

对于节点 \(x\) 和其子节点 \(y_1,y_2,y_3,\cdots,y_k\)，有：

\[dp_{x,0}\leftarrow dp_{x,0}+\sum_{i=1}^k\min(dp_{y_i,0}-1,dp_{y_i,1})\\ dp_{x,1}\leftarrow dp_{x,1}+\sum_{i=1}^k\min(dp_{y_i,1}-1,dp_{y_i,0})\\ \]

以 \(dp_{x,0}\) 为例：

• \(dp_{y_i,0}-1\)：子节点染成 \(0\)，则可以继承 \(x\) 的颜色 \(0\)，因此减去 \(1\)。
• \(dp_{y_i,1}\)：子节点染成 \(1\)，不可以继承 \(x\) 的颜色 \(0\)， 因此直接加法。

最后取最小值即可。

\(dp_{x,1}\) 同理可得。

根节点的不同与答案无关

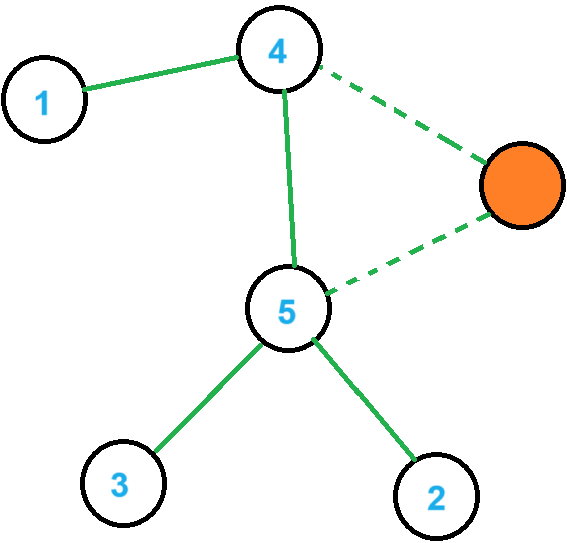
如图，答案合并至 \(4,5\) 时，完全可以构造一个不存在的节点（图中橙色节点），并连接 \(4,5\)，将答案合并到父节点橙色节点上，则最终答案也是一样的。

即 \(4,5\) 作根时，答案相同。

推广到非叶节点上，即根节点的不同与答案无关。

AC 代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int M=1e4,N=5021;
int m,n,c[N+1];
struct graph{
	struct edge{
		int v,r;
	}a[2*(M-1)+1];
	
	int h[M+1],d[M+1];
	void create(int u,int v){
		static int top;
		a[++top]={v,h[u]};
		h[u]=top;
		d[u]++;d[v]++;
	}
}g;
//dp[x][i]:点x标成颜色i的最少染色数量 
int dp[M+1][2];
void dfs(int x,int fx){
	for(int i=g.h[x];i>0;i=g.a[i].r){
		if(g.a[i].v==fx)continue;
		dfs(g.a[i].v,x);
		dp[x][0]+=min(dp[g.a[i].v][0]-1,dp[g.a[i].v][1]);
		dp[x][1]+=min(dp[g.a[i].v][1]-1,dp[g.a[i].v][0]);
	}
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	scanf("%d %d",&m,&n);
	for(int i=1;i<=m;i++){
		dp[i][0]=dp[i][1]=1;
	}
	for(int i=1;i<=n;i++){
		scanf("%d",c+i);
		dp[i][!c[i]]=2147483647;
	}
	for(int i=1;i<m;i++){
		int u,v;
		scanf("%d %d",&u,&v);
		g.create(u,v);
		g.create(v,u);
	}
	int root;
	for(int i=m;i>n;i--){
		if(g.d[i]>1){
			root=i;
			break;
		}
	}
	dfs(root,0);
	printf("%d\n",min(dp[root][0],dp[root][1]));
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}