题解:[NOIP2016 提高组] 蚯蚓
前置结论
结论
对于整数 \(x_1,x_2\) ,当 \(x_1\geq x_2,0<p<1\) 时有:
- \(\lfloor px_1 \rfloor \geq \lfloor px_2 \rfloor\)
- \(x_1 -\lfloor px_1 \rfloor \geq x_2- \lfloor px_1 \rfloor\)
证明
结论 \(1\) 显然得证。
结论 \(2\) 证明参见此处。以下为转载内容。
2024 年 7 月更新:新版蓝书受我反馈,已经更正此问题。
本题中所有题解的单调性正确性似乎都有或多或少的问题,在这里我给出一个严谨的单调性证明。
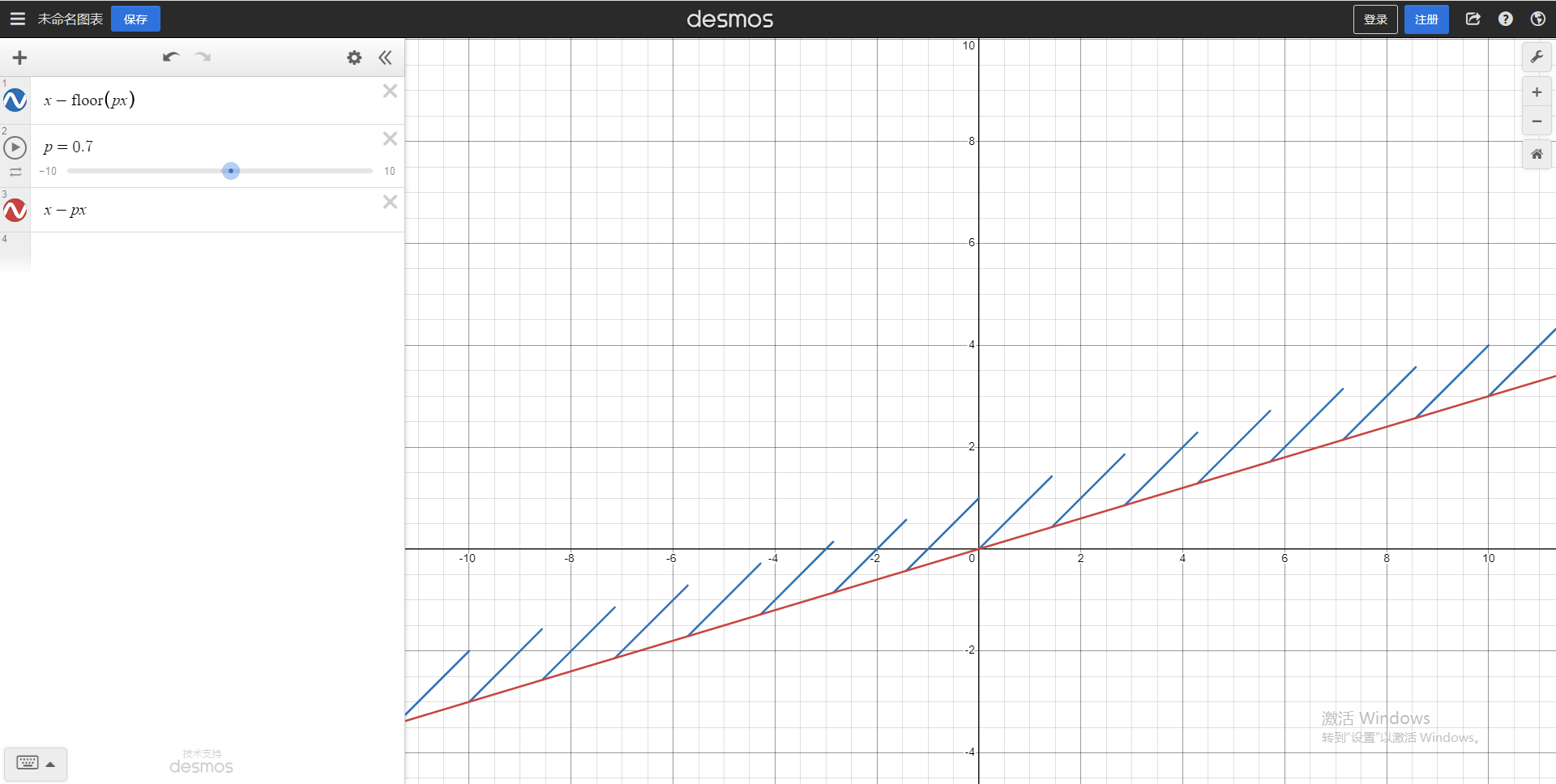
首先:\(x - \lfloor px \rfloor\) 这个函数并不是单调不降的,它只在整点上单调不降,可以在 desmos 中画一个 \(x - \lfloor 0.9x \rfloor\) 的函数试试看,你会发现它并没有单调性。当然,\(x - px\) 有单调性。
所以一切直接抛开下取整对单调性的证明是没有任何道理的,这就叉掉了本题大量题解,包括但不限于第一篇题解。
同时,一切没有用到 \(x_1\),\(x_2\) 这两个数为整数这个性质就证出了这个函数的单调性的都是伪证,本题疑似所有题解全都是伪证。lyd 蓝书上的证明也是伪证,具体原因见下。
前置知识:
- 下取整函数单调不降,即对于 \(x_1 < x_2\) 有 \(\lfloor x_1\rfloor \le \lfloor x_2 \rfloor\);
- 整数可以自由移入移出下取整函数,即对于 \(z \in \mathbb Z\),有 \(\lfloor x \rfloor + z = \lfloor x + z \rfloor\)。
- 注意:负号不能随便移入移出,\(\lfloor -3.4 \rfloor \ne - \lfloor 3.4 \rfloor\)。
- 关于这点很容易犯的一个错误就是对于 \(z \in \mathbb Z\),有\(\lfloor z - x \rfloor = z - \lfloor x \rfloor\),事实上这点根本不成立,举个反例:\(\lfloor 1 - 0.3 \rfloor \ne 1 - \lfloor 0.3\rfloor\)。
- 刚刚这条错误就是很多伪证的错误原因所在,包括 lyd 蓝书的证明也存在这个伪证。
真正证明:
命题:对于 \(x_1, x_2 \in \mathbb Z, x_1 \ge x_2, 0< p < 1\),有 \(x_1 - \lfloor px_1 \rfloor \ge x_2 - \lfloor px_2 \rfloor\)。
证明:\(x_1 \ge x_2 \land x_1, x_2 \in \mathbb Z\),因此 \(x_1 - x_2 \in \mathbb N\)。又因为 \(0 <p < 1\),所以:
\[\begin{aligned} x_1 - x_2 &\ge p(x_1 - x_2)\\ x_1 - x_2 + p x_2 & \ge px_1 \\ \lfloor px_2 + (x_1 - x_2) \rfloor & \ge\lfloor px_1 \rfloor \\ \lfloor px_2 \rfloor + (x_1 - x_2) & \ge \lfloor px_1 \rfloor \\ x_1 - \lfloor px_1 \rfloor & \ge x_2 - \lfloor px_2 \rfloor \end{aligned} \]证明出了这一点的单调性之后,事实上我们就解决了 \(q = 0\) 的单调性问题,接下来解决 \(q \ge 0\) 的。
我们假设某一秒,我们切开了一个数 \(x_1\),下一秒,我们切开了一个数 \(x_2 + q\)。\(x_2 + q\) 在上一秒时为 \(x_2\),因此 \(x_1 \ge x_2\)。我们的证明目标是 \(\lfloor px_1\rfloor+ q \ge \lfloor p(x_2 + q)\rfloor\) 和 \(x_1 - \lfloor px_1\rfloor+ q \ge x_2 + q - \lfloor p(x_2 + q)\rfloor\)。
需要注意这个证明目标也有很多题解搞错,lyd 蓝书此处的证明存在上面所说的问题(那条假结论)。
对于第一条:\(\lfloor px_1\rfloor+ q = \lfloor px_1 + q\rfloor \ge \lfloor px_2 + pq\rfloor = \lfloor p(x_2 + q)\rfloor\)。
对于第二条:\(x_1 - \lfloor px_1\rfloor+ q \ge x_2 +q - \lfloor px_2\rfloor \ge x_2 + q - \lfloor p(x_2 +q) \rfloor\)。这里第一个不等号用了 \(q = 0\) 的证明结论。
不知道你们有没有这个疑问,我补一下。https://www.luogu.com.cn/discuss/551666
其中,\(\color{blue}{x -\lfloor px\rfloor}\color{black}{,}\ \color{red}{x-px}\) 图像如此:
处理切割
数据结构
维护三个队列 \(Q_1,Q_2,Q_3\):
- \(Q_1\) 为未曾切割的蚯蚓;
- \(Q_2\) 为切割时形如 \(\lfloor px \rfloor\) 的蚯蚓;
- \(Q_3\) 为切割时形如 \(x- \lfloor px \rfloor\) 的蚯蚓。
操作
模拟题意:每次取最长蚯蚓进行切割。
首先维持 \(Q_1\) 单调不增,然后根据前置结论 \(2\) ,取最长蚯蚓进行切割所得的两条蚯蚓也比其他蚯蚓切割所得蚯蚓长。
举个例子:
蚯蚓长为 \(10,8,7\),\(p=0.3\)。则切割所得蚯蚓长为 \((3,7),(2,6),(2,5)\),括号表示由同一蚯蚓切割所得。
这样,我们每次在 \(Q_1,Q_2,Q_3\) 里查询最大值,切割后加入 \(Q_2,Q_3\) 就可以维持 \(Q_2,Q_3\) 单调。那么我们只需要取队首比较即可。
输出
第一行
输出也只需要 \(i \in [1,m]\) 模拟每一秒,\(i \bmod t=0\) 时输出队首即可。
第二行
从大到小查找队首输出并出队即可。
考虑到蚯蚓每一秒都会增长 \(q\),我们考虑是否可能 \(\mathcal O(1)\) 处理。
不妨令 \(i\) 秒时,\(q=pl\)。
那么我们记录蚯蚓加入队列时的已增加长度 \(pl'\),最后用原有长度加上 \(pl-pl'\) 即可。
那么我们只需要在加入队列时,加入 \(\lfloor px \rfloor-pl'\) 即可。
由于所有蚯蚓都减去了 \(pl'\),并不影响 \(Q_1,Q_2,Q_3\) 的单调性。
AC代码
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
const int M=7e6;
int n,m,q,u,v,t;
//Q:手写队列(节约空间)
int Q[4][M+1],front[4],rear[4];
bool cmp(int a,int b){
return a>b;
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
scanf("%d %d %d %d %d %d",&n,&m,&q,&u,&v,&t);
for(int i=1;i<=n;i++)scanf("%d",&Q[1][i]);
front[1]=front[2]=front[3]=1;
rear[1]=n;
sort(Q[1]+1,Q[1]+n+1,cmp);//单调不增
int pl=0;
//第一行
for(int i=1;i<=m;i++){
//查找队首最大值
int o,Max=-2147483648;
for(int j=1;j<=3;j++){
if(front[j]<=rear[j]&&Q[j][front[j]]>Max){
Max=Q[j][front[j]];
o=j;
}
}front[o]++;//出队
Max+=pl;pl+=q;
int x=1ll*Max*u/v;
//切割并入队
Q[2][++rear[2]]=x-pl;
Q[3][++rear[3]]=Max-x-pl;
if(i%t==0)printf("%d ",Max);//输出
}putchar(10);//换行
//第二行
for(int i=1;i<=m+n;i++){
//从大到小查找、输出即可。
//同理
int o,Max=-2147483648;
for(int j=1;j<=3;j++){
if(front[j]<=rear[j]&&Q[j][front[j]]>Max){
Max=Q[j][front[j]];
o=j;
}
}front[o]++;
if(i%t==0)printf("%d ",Max+pl);
}
/*fclose(stdin);
fclose(stdout);*/
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号