题解：[ROIR 2025] 寻找宝藏

题目传送门

题意分析

本文中记 \(x_i\) 为第 \(i\) 列的扫描结果，即 \(x_i\) 为原题中 \(b_i\)。同时，以下推导均不考虑取模。

DP 状态设计

注意到 \(k\leq7\)，且是计数类问题，因此考虑与 \(k\) 有关的涉及状压的 DP。

如图，扫描仪的扫描区域其实就可以视作一个类似于三角形的区域在图上向右滑动。而第 \(i\) 列的扫描结果与第 \(i-1\) 列的扫描结果的差异就源于图中红色、绿色、蓝色等部分的斜线。因此可以考虑针对这些斜线设计 DP 状态。

设 \(\textit{dp}_{i,j_1,j_2,\cdots,j_{k-1}}\) 表示处理第 \(i\) 列，\(1\sim i\) 列均合法，且从外往内数第 \(l\) 层斜线的矿产数量为 \(j_l\) 时（不包括只有一个点的那条斜线，那会被包含到第 \(i\) 列中特殊处理）的合法表格数，也代表这一个扫描仪的状态。

DP 状态转移

同样由于 \(k\leq7\)，因此可以 \(\mathcal O\left(2^k\right)\) 枚举第 \(i\) 列的矿产情况，记为 \(S\)。

记 \(\operatorname{popcount}(S)\) 表示 \(S\) 含有的矿产数量，即代码实现中 \(S\) 的二进制位 \(1\) 的数量。

假设 \(\textit{dp}_{i-1,j_1,j_2,\cdots,j_{k-1}}\) 已知，考虑如何转移到当前 \(S\) 对应的状态 \(\textit{dp}_{i,j'_1,j'_2,\cdots,j'_{k-1}}\)。

首先，当且仅当 \(j_1+j_2+\cdots+j_{k-1}+\operatorname{popcount}(S)=x_i\) 时，\(\textit{dp}_{i,j'_1,j'_2,\cdots,j'_{k-1}}\) 才可能从 \(\textit{dp}_{i-1,j_1,j_2,\cdots,j_{k-1}}\) 转移，否则不合法。

记 \(S_p\) 表示第 \(p\) 行是否有矿产，即代码实现中 \(S\) 的二进制第 \(p-1\) 位。

以 \(k=3\) 为例，\(\textit{dp}_{i-1,j_1,j_2}\) 向右滑动，如图，最外层的 \(j'_1\) 就变成了 \(j_2+S_3\)。

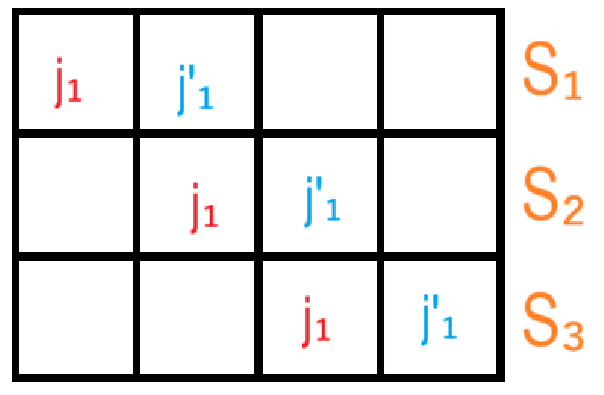
推广到其他情况，都是类似的处理方式，假设 \(k=7\)，有：

\[j'_1=j_2+S_6\\ j'_2=j_3+S_5\\ j'_3=j_4+S_4\\ j'_4=j_5+S_3\\ j'_5=j_6+S_2\\ j'_6=S_1\\ \]

这里的 \(j'_6\) 即代表扫描仪区域右上角那一个大小为 \(1\times1\) 的斜线，与 \(i-1\) 的状态无关，因此无需放入 DP 状态。

记：

\[A=\textit{dp}_{i,j'_1,j'_2,\cdots,j'_{k-1}}\\ B=\textit{dp}_{i,j_1,j_2,\cdots,j_{k-1}} \]

则有：

\[A\leftarrow A+B \]

高维部分处理

但是，考虑到 \(k=7\) 不一定成立，那么也许 DP 状态就会更改。

但是这其实不重要，既然高维是多余部分，不影响答案，那么久集体取一个特殊值即可。

例如令 \(j'_1,j'_2,\cdots,j'_{k'}\in [k+1,7]\) 维部分的 \(dp_{i,j_1,\cdots,j_{k-1},j'_1,\cdots,j'_{k'}}\)，\(j'_1=j'_2=\cdots=j'_{k'}=0\) 即可。

---

当然，你要是分 \(7\) 种情况处理也是可以的。模拟赛有人这么写，AC 了。

时间复杂度

直接枚举的复杂度是 \(\mathcal O\left(nk^k2^k\right)\)。

但是考虑到可以在循环枚举的时候就保证 \(j_1+j_2+\cdots+j_l\leq x_i\)，这样的话，枚举 \(j_1,j_2,\cdots,j_{k-1}\) 的复杂度就降低到了 \(\mathcal O(k!)\)。

最终复杂度：\(\mathcal O\left(nk!2^k\right)\)。

其实还有一个 \(\mathcal O\left(\log S\right)=\mathcal O(k)\) 求 \(\operatorname{popcount}(S)\) 的复杂度没算，但是可以预处理或记忆化，所以不用算。

AC 代码

如果你担心炸空间，可以将空间开成 \(\mathcal O(nk!)\) 的，而不是 \(\mathcal O\left(k^k\right)\)。实际上，还可以使用滚动数组滚掉，因此最优空间复杂度为 \(\mathcal O(k!)\)。

//#include<bits/stdc++.h>
#include<algorithm> 
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=200,K=7,B=(K+1)*K>>1,P=1e9+7;
int n,k,x[N+1];
int dp[2][K+1][K+1][K+1][K+1][K+1][K+1];
int popcount(int x){
	int ans=0;
	while(x){
		ans++;
		x^=x&-x;
	}
	return ans;
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	
	cin>>n>>k;
	for(int i=1;i<=n;i++){
		cin>>x[i];
		if(x[i]>(k*(k+1)>>1)){
			cout<<'0'<<endl;
			return 0;
		}
	}
	bool mode;
	dp[mode][0][0][0][0][0][0]=1;
	int ans=0;
	for(int i=1;i<=n;i++){
		mode=!mode;
		memset(dp[mode],0,sizeof(dp[mode]));
		for(int a=0;!a||a<=min(6,x[i])&&k>=7;a++){
			for(int b=0;b<=min(5,x[i]-a)&&k>=6||!b;b++){
				for(int c=0;c<=min(4,x[i]-a-b)&&k>=5||!c;c++){
					for(int d=0;d<=min(3,x[i]-a-b-c)&&k>=4||!d;d++){
						for(int e=0;e<=min(2,x[i]-a-b-c-d)&&k>=3||!e;e++){
							for(int f=0;f<=min(1,x[i]-a-b-c-d-e)&&k>=2||!f;f++){
								for(int S=0;S<(1<<k);S++){
									int pl=popcount(S);
									if(pl+a+b+c+d+e+f!=x[i]){
										continue;
									}
									int pa=0,pb=0,pc=0,pd=0,pe=0,pf=0;
									if(k>=7){
										pa=b+(S>>5&1);
									}
									if(k>=6){
										pb=c+(S>>4&1);
									}
									if(k>=5){
										pc=d+(S>>3&1);
									}
									if(k>=4){
										pd=e+(S>>2&1);
									}
									if(k>=3){
										pe=f+(S>>1&1);
									}
									if(k>=2){
										pf=S&1;
									}
									int &A=dp[mode][pa][pb][pc][pd][pe][pf],&B=dp[!mode][a][b][c][d][e][f];
									A=(A+B)%P;
									if(i==n){
										ans=(ans+B)%P;
									} 
								}
							}
						}
					}
				}
			}
		}
	}
	cout<<ans<<'\n';
	return 0;
	
	cout.flush();
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}