笛卡尔树

笛卡尔树

luogu P5854 【模板】笛卡尔树

定义

笛卡尔树是一种二叉树，每一个节点有两个权值 \(a,b\)，要求所有节点的 \(a\) 满足 BST（二叉查找树）的性质，\(b\) 满足堆^[1]的性质。若 \(a,b\) 确定，则笛卡尔树是确定的。

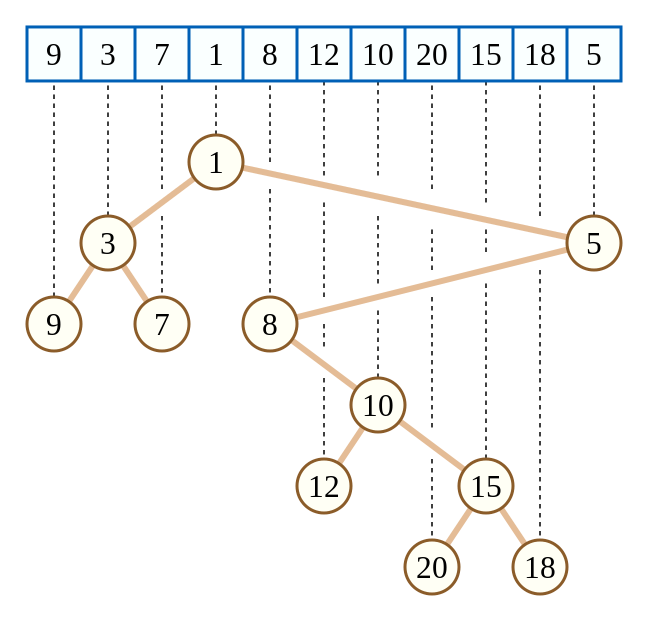
如图，取 \(a=\langle1,2,3,4,5,6,7,8,9,10,11\rangle,b=\langle9,3,7,1,8,12,10,20,15,18,5\rangle\)，即可构建上图。下标满足 BST 性质，值满足堆的性质。

---

同时，Treap 实际上就是一种笛卡尔树。

构建

笛卡尔树可以做到 \(\mathcal O(n)\) 构建。

考虑按照满足 BST 性质的 \(a\) 升序插入节点 \(x\)，那么节点 \(x\) 要么是根节点，要么是最右端的节点。

考虑维护一条「右链」，即只包含根节点和右子节点的链。

插入节点 \(x\) 时，找右链上的节点 \(y\) 使得 \(b_y\leq b_x\) 且 \(b_y\) 最大（\(y\) 最深），则 \(x\) 为 \(y\) 的右子节点，\(y\) 原来的右子节点 \(v\) 现在为 \(x\) 的左子节点。

特别地，若不存在 \(b_y\leq b_x\)，则 \(x\) 为根节点。

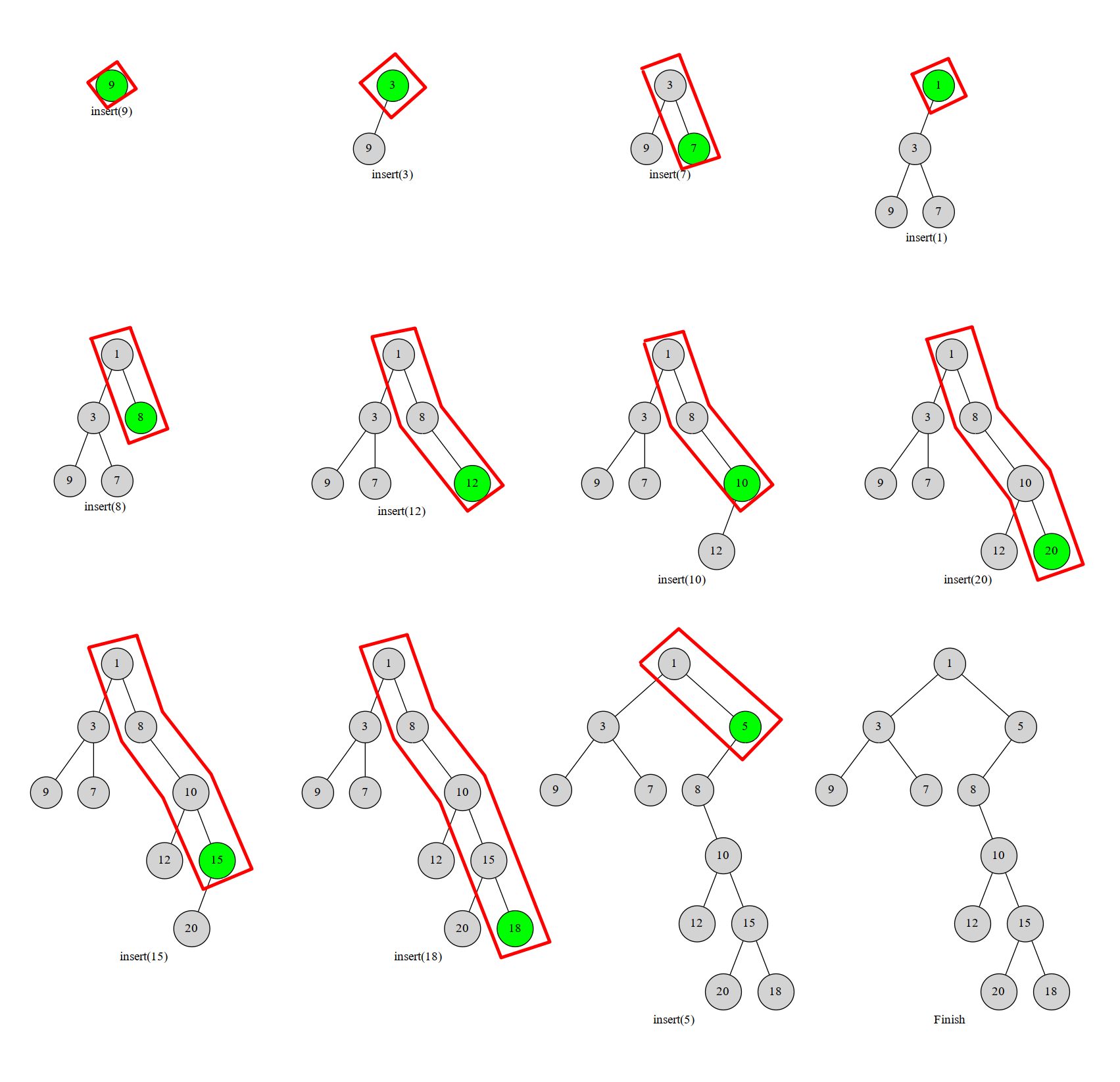
单调栈维护右链

可以发现，右链上的 \(b\) 值单调不降。因此插入 \(b_x\) 时，若 \(b_y>b_x\)，\(y\) 一定不在新的右链里。

因此单调栈维护右链，即维护单调不降的序列，记录最后一个出栈的节点 \(p\)，\(p\) 即为 \(x\) 的左子节点。

每个节点至多入栈/出栈 \(1\) 次，时间复杂度 \(\mathcal O(n)\)。

vector<int>s;
for(int i=1;i<=n;i++){
    int p=0;
    while(s.size()&&b[s.back()]>b[i]){
        p=s.back();
        s.pop_back();
    }
    if(s.size()){
        r[s.back()]=i;//记录右子节点
    }
    l[i]=p;//记录左子节点
    s.push_back(i);
}

luogu P5854 【模板】笛卡尔树

参考代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
typedef long long ll;
constexpr const int N=1e7;
int n,p[N+1],l[N+1],r[N+1];
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>p[i];
	}
	vector<int>s;
	for(int i=1;i<=n;i++){
		int pl=0;
		while(s.size()&&p[s.back()]>p[i]){
			pl=s.back();
			s.pop_back();
		}
		if(s.size()){
			r[s.back()]=i; 
		}
		l[i]=pl;
		s.push_back(i);
	}
	ll ans=0;
	for(int i=1;i<=n;i++){
		ans^=i*(l[i]+1ll);
	}
	cout<<ans;
	ans=0;
	for(int i=1;i<=n;i++){
		ans^=i*(r[i]+1ll);
	}
	cout<<' '<<ans;
	
	cout.flush();
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

[TJOI2011] 树的序

将一棵二叉查找树的键值插入序列称为树的生成序列，现给出一个生成序列，求与其生成同样二叉查找树的所有生成序列中字典序最小的生成序列。

生成序列为 \(k_1,k_2,\cdots,k_n\) 且为一个 \(1\sim n\) 的排列。

考虑一下把树建出来，容易发现每个点 \(x\) 其实都有两个键值 \(k_x,t_x\)，\(t_x\) 表示 \(x\) 是第几个插入的。由 BST 的生成方式，若 \(x\) 是 \(y\) 的祖先，则有 \(t_x<t_y\)。

因此 \(t_x\) 需要满足小根堆的性质，不难发现这是一棵笛卡尔树。那么就可以 \(\mathcal O(n)\) 建树。

建树时，按照满足 BST 性质的 \(k_x\) 从小到大插入节点。因为满足排列，可以直接桶排。

这样，你就 \(\mathcal O(n)\) 建好了树。之后先序遍历输出满足 \(t_x\) 即可，即数组下标。

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
typedef long long ll;
constexpr const int N=1e5;
int n,a[N+1],l[N+1],r[N+1];
void print(int p){
	if(!p){
		return;
	}
	cout<<p<<' ';
	print(l[p]);
	print(r[p]);
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	
	cin>>n;
	for(int i=1;i<=n;i++){
		int x;
		cin>>x;
		a[x]=i;
	}
	vector<int>s;
	for(int i=1;i<=n;i++){
		int pl=0;
		while(s.size()&&a[s.back()]>a[i]){
			pl=s.back();
			s.pop_back();
		}
		if(s.size()){
			r[s.back()]=i;
		}
		l[i]=pl;
		s.push_back(i);
	}
	print(s[0]);
	
	cout.flush();
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

---

1. 小根/大根堆均可，本文仅讨论小根堆。 ↩︎