概论

正态分布

说起正态分布（随机变量X服从正态分布），仿佛很熟悉又有点说不出来什么的感觉，更是和“高斯分布”划等号，于是有了这篇小报告。

什么是随机变量？

随机变量的定义：随机变量是定义在随机试验的样本空间（随机试验的所有可能结果组成的集合，即所有样本点）上的单值实值函数。

（1、记住了，实质上是一个函数，自变量是所有样本点）

（2、函数就有离散函数和连续这样的区分，对应于离散随机变量和连续随机变量）

什么是正态分布？什么是“分布”、概率密度？有什么应用、意义？

1、对于离散的（一维）随机变量，如果是离散型随机变量（随机变量的取值有限个或者无限可列个），通过分布律（pmf：probability mass function随机变量的所有可能取值以及对应的概率）掌握随机变量的统计规律；

此时，可以引入对于连续型随机变量的统计规律的描述：首先，连续型随机变量（非离散型：随机变量的取值无限、不可列）不能一一列出；其次，对于随机变量取某一实数值的概率分布情况，并不是常常关心的量（实际上没有什么意义，等于0）。我们常常关心的是随机变量的值落在某个区间内的概率！于是，定义出分布函数（一个连续随机变量X取值小于等于某一特定实数x的概率）。

接着，可以引出概率密度函数（pdf：probability density function），概率密度函数是分布函数的导函数（如果存在），而分布函数是随机变量大于某个值的概率....。（意义：某个实数坐标区间上概率密度函数与坐标轴围成的面积就是随机变量的取值落在该区间上的概率大小！，或者说单纯讲概率密度是没有意义的...）

2、正态分布：连续随机变量X的分布情况满足正态分布，也就是概率密度函数f(x)等于那个公式f(x)=1/sqrt(2pi)sigma·exp((x-u)²/2sigma²)，x定义域是整个实数轴，σ（sigma）是x的标准差（方差的算术平方根），u是X的均值。我们称X服从参数为u，σ的正态分布或者说高斯分布。X~N(u,σ²)。

3、一维正态分布的性质、应用：

一维的正态分布（高中的时候学的！）

性质有：1、概率密度曲线（以随机变量x为自变量（横坐标）、概率密度f(x)为纵坐标）关于x=u对称、并且在x=u取最大值；

2、曲线越”矮（也意味着”胖“）胖”，表示着该随机变量的分布越分散；曲线越“高（也意味着瘦，因为曲线与坐标轴围成的总面积等于1）瘦”，表示分布越集中；

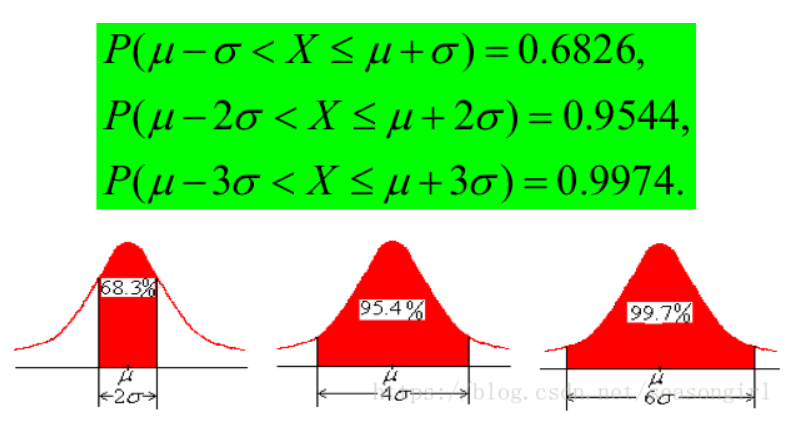
3、三个重要的区间面积值：0.6826、0.9544、0.9974（3σ原则，区间外的概率小于5%！）；

4、u是位置参数、σ越大曲线越矮胖（分布越分散=方差σ²越大）；

5、u=0,σ=1时，正态分布又称为标准正态分布，概率密度和分布函数用φ（x)和Φ（x）表示，Φ（0）=0.5、Φ(x)=1-Φ（-x）、φ（x）=1/sqrt(2pi)·exp()。

 

 

 

什么是高斯分布？多维高斯分布？

高斯分布是正态分布的推广，包含正常的（特征函数存在、概率密度函数也存在）与退化的（特征函数存在、概率密度函数不存在）正态分布。

谈到多维高斯分布，就不得不认识到“多维”的含义。一维的随机变量（一个样本点对应一个随机变量的实数值），多维（n维）的随机变量（也称为一个n维的随机向量）（一个样本点也就是一个试验的结果，对应了多个（n个）随机变量的实数值，eg：一个学生考试成绩，对应了数学分数、语文分数、.....多个随机变量的....）。

多维高斯分布，联合分布情况

协方差的概念，

矩阵的逆的概念，

代数余子式的概念，

特征函数的概念，