P7417 [USACO21FEB] Minimizing Edges P 解题报告

P7417 [USACO21FEB] Minimizing Edges P 解题报告

首先建图需要注意的是可以完全重构。观察到对于每个点有用的信息仅有奇偶最短路长度，因为得到任意一条最短长度 \(L\) 就相当于得到了所有 \(L+2K\)，可以反复走一条边。

我们用一个二元组来表示所有最短路为 \(x\)，次短且不同奇偶的路为 \(y\) 的点的集合，即 \((x,y),x<y\)，点的个数为 \(siz(x,y)\)。每个点的奇偶最短路容易用 BFS 得出，然后把相同的 \((x,y)\) 归入同一个集合中，我们考虑转移的问题。如果要重构一个图，那么想要让一个集合中所有点符合条件，转移有以下几个来源：

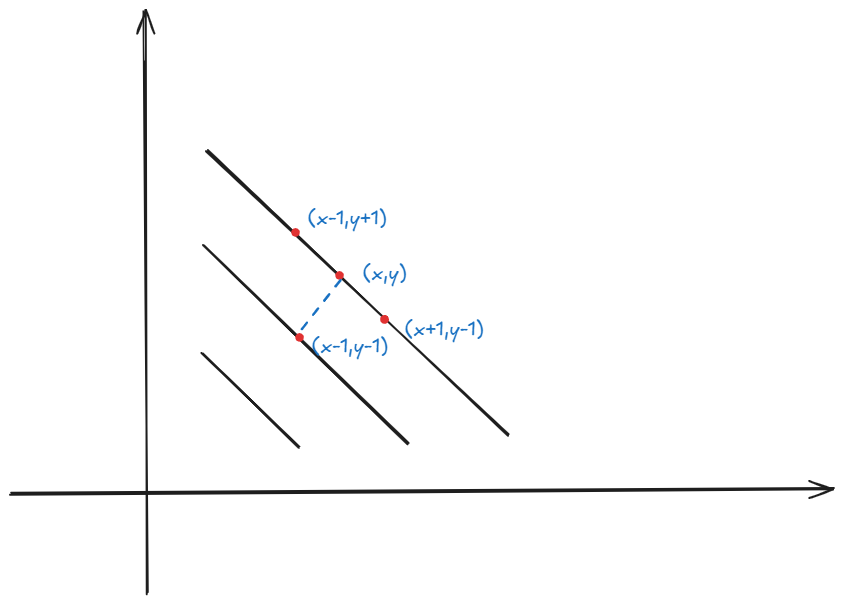
1. \((x,y)\leftarrow (x-1,y-1)\)

只需要建一条边，让最短和次短路数据依次覆盖即可。这种方案是最好的，因为耗费边数最小。

2. \((x,y)\leftarrow (x-1,y+1),(x+1,y-1)\)

值得注意的是，这个转移是唯一的。\((x-1,y+1)\) 用于给到最短路 \(x\)，\((x+1,y-1)\) 用于给到最短路 \(y\)，那么为什么另一维都是确定的？因为和 \((x,y)\) 相连，意味着该点那个维度最长也就是从 \((x,y)\) 多走一条边。由于 \(x,y\) 奇偶性不同，所以不可能出现类似 \((x-1,y)\) 的情况。

天才的构造！然后让我们开始分类讨论转移：

我们考虑连一些同层边，使得即使没有直接从上一层的 \((x-1,y-1)\) 连过来的边，也可以因为同一层的某个节点连了上一层，连到这个节点也可以达到相同的效果。我们模拟一下这个过程，可以发现：单独考虑一个集合 \((x,y)\)，假如 \((x-1,y+1)\) 打算给它连的边数为 \(c\)，可以分两种情况。

1. \(c<siz(x,y)\)，意味着这些连接不能完全覆盖所有节点，那么还有一部分节点没有被覆盖。分类讨论，如果存在 \((x-1,y-1)\)，那么可以直接向它们连接 \(siz(x,y)-c\) 条边（耗费为 \(1\)），否则就要再向 \((x-1,y+1)\) 连相应数量的边，然后准备给 \((x+1,y-1)\) 连 \(siz(x,y)\) 条边（耗费为 \(2\)）。

2. \(c\geq siz(x,y)\)，意味着这些连接过度覆盖了所有节点，这时候我们可以选择把这些节点接到 \((x-1,y-1)\) 或者 \((x+1,y-1)\) 上，但是我们必须全部接后者，且接 \(siz(x,y)\) 条边，具体原因等会儿会解释。

然后会发现一定会到达一个边界，使得要么有 \(x+1=y\)，即此时 \((x+1,y-1)\) 和 \((x,y)\) 等价，即相当于自己连自己，这时候我们可以把最后这个点集里的点两两匹配，多出来那一个点自己跟自己连（耗费 \(\lceil \frac{c}{2}\rceil\)）。要么什么也没有，此时只能让每个点都连接自己，耗费 \(c\)。

我们不难发现，在步骤 2 中，其实对于每一个点，要么耗费 \(1\) 的代价往 \((x-1,y-1)\) 传，要么耗费 \(1\) 的代价往 \((x+1,y-1)\) 传，这两种在过度覆盖的条件下是等效的，因为无论如何你都已经给集合中每个点都连了一条边。哪种会更优呢？因为有可能传到 \(x+1=y\) 的边界，这时候只需要每个点 \(\frac{1}{2}\) 的代价就能消掉，那么显然我们在之前需要给这个边界更多的点，才能尽量减少费用，所以我们在步骤 2 中选择往下传。

在具体代码实现中，每次处理一个集合我们只给 \(ans\) 累加向 \((x-1,y+1),(x-1,y-1)\) 连的边数，对于 \((x+1,y-1)\) 丢进一个 \(left\) 中后面再处理。也就意味着步骤 1 中，你要么向 \((x-1,y-1)\) 要么向 \((x-1,y+1)\) 连了边，每个节点必占其一，无论如何本层花费都是 \(siz(x,y)\)。

最后注意如果当前集合有一个点 \(1(x=0)\)，且这个集合只可能有这一个节点，那么在步骤 1 中我们需要排除这个特殊情况，它不需要向 \((x-1,y-1),(x-1,y+1)\) 任意一个连边，也找不到。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
const int N=2e5+5,INF=1e9;
int n,m,dis[N][2];
vector<int>G[N];
PII q[N];
int hd=1,tl;
void bfs(){
	for(int i=1;i<=n;i++)dis[i][0]=dis[i][1]=INF;
	dis[1][0]=0;
	hd=1,tl=0;
	q[++tl]=make_pair(1,0);
	while(hd<=tl){
		int u=q[hd].first;
		int o=q[hd].second;
		hd++;
		for(int v:G[u]){
			if(dis[u][o]+1<dis[v][o^1]){
				dis[v][o^1]=dis[u][o]+1;
				q[++tl]=make_pair(v,o^1);
			}
		}
	}
}
int main(){
	int T;
	scanf("%d",&T);
	while(T--){
		map<PII,int>siz;
		vector<PII>p;
		scanf("%d%d",&n,&m);
		for(int i=1;i<=n;i++)
			G[i].clear();
		for(int i=1;i<=m;i++){
			int u,v;scanf("%d%d",&u,&v);
			G[u].push_back(v);
			G[v].push_back(u);
		}
		bfs();
		bool tf=0;
		for(int i=1;i<=n;i++)
			if(dis[i][0]==INF||dis[i][1]==INF)
				tf=1;
		if(tf){
			printf("%d\n",n-1);
			continue;
		}
		for(int i=1;i<=n;i++){
			int x=dis[i][0],y=dis[i][1];
			if(x>y)swap(x,y);
			PII my=make_pair(x+y,x);
			p.push_back(my);
			siz[make_pair(x,y)]++;
		}
		sort(p.begin(),p.end());
		p.erase(unique(p.begin(),p.end()),p.end());
		LL ans=0;
		int lef=0;
		for(PII i:p){
			int x=i.second,y=i.first-i.second;
			PII G=make_pair(x,y);
			int F=siz[G];
			if(F>lef){
				ans+=F*(x>0);
				if(!siz[make_pair(x-1,y-1)])lef=F;
			}
			else {
				ans+=lef;
				lef=F;
			}
			if(!siz[make_pair(x+1,y-1)]){
				if(x+1==y)ans+=(lef+1)/2;
				else ans+=lef;
				lef=0;
			}
		}
		printf("%lld\n",ans);
	}
	return 0;
}