（笔记）DFA 简介字符串相关 Border KMP AC 自动机 Manacher 回文自动机 PAM

DFA 确定性有限状态自动机

严谨介绍请前往OI-wiki

如果把解决问题的过程画成一个流程图，那么一个确定性有限状态自动机就类似一个处理机器，可以用一个有向图来表示自动机不同状态之间的转移。不妨令这个有向图的点集为 \(Q\)，可能的输入信号（字符集）为 \(\Sigma\)，转移函数 \(\delta\)（可理解为有向图上的边集），起始状态为 \(q_0\in Q\)，终止状态集合为 \(F\subseteq Q\)。那么这个 DFA 就可以表示为 \((Q,\Sigma,\delta,q_0,F)\)。

DFA 不是数据结构，不是算法，而是数学模型。

一个 DFA 能够接受一段信号序列的充分必要条件是：

对于 DFA \(M=(Q,\Sigma,\delta,q_0,F)\)，一段信号序列 \(w=w_1w_2\dots w_n\in\Sigma^{*}\) 存在一段唯一对应的状态序列 \(r_0,r_1,\dots,r_n\)，使得：

\(r_0=q_0\)
\(\forall i\in[1,n],\delta(r_{i-1},w_i)=r_i\)
\(r_n\in F\)

下面的举例可以阅读下文后理解。

具体来说，拿字典树 Trie 举例，\(Q\) 就是所有节点（状态）的集合，\(\Sigma\) 就是 \(26\) 个字母的集合，\(\delta(q,c)\) 的转移表示在状态 \(q\) 后加入新字符 \(c\) 所得到的状态，\(q_0\) 就是根节点，\(F\) 就是所有插入 Trie 中字符串的末尾节点的集合。

再拿 KMP 举例，这里每个节点（状态）表示一段前缀，比较特殊的是它的转移，有一个表示 \(\text{mxBd}\) 的 \(\texttt{Fail}\) 指针。那么它增加一个字符的转移就是：

\[\delta(q,c)= \begin{cases} q+1 & S[q+1]=c\\ 0 & q=0\land S[q+1]\neq c\\ \delta(\texttt{Fail}_q,c) & \text{otherwise} \end{cases} \]

扩展：NFA 是非确定性有限状态自动机，处理信号序列的过程可以类比找子序列（不一定要连续），允许信号序列中出现若干个空字符，即字符集 \(\Sigma_{\epsilon}^{*}\) 是包含空字符的，而且由于这些空字符的存在，NFA 走的状态序列并不是唯一的，它相当于同时跑很多个 DFA，然后 \(r_n\) 也可能有很多种。

以下内容参考资料：command_block 讲义

Border

对于长度为 \(n\) 的字符串 \(S\)，如果存在严格前缀（不包含整串）\(S[:i]=S[n-i+1:]\)，那么记 \(S\) 有一个长 \(i\) 的 \(\text{Border}\)（简写为 \(\text{Bd}\)），且记最长的 \(\text{Border}\) 集合为 \(\text{mxBd(S)}\)。

Theorem：\(\text{Bd}\) 的 \(\text{Bd}\) 是 \(\text{Bd}\)，任何 \(S\) 的 \(\text{Bd}\) 都可以通过若干次 \(\text{mxBd}\) 的 \(\text{mxBd}\) 递推表示。这和 \(fail\) 指针是类似的。

KMP

通过双指针的方法快速 \(O(n)\) 求出 \(S\) 及其所有前缀的 \(\text{Bd}\)（长度），然后实现字符串匹配。其中 \(z[i]\) 记录的是 \(S[:i]\) 的最长 \(\text{Bd}\) 长度（\(i\to z[i]\) 的连边称为 \(\texttt{Fail}\) 指针）。

观察到，在匹配扩展的过程中，如果令当前匹配区间为 \([l,r]\)（即有 \(S[l:r]=S[1,r-l+1]\)），那么对于每个 \(i\)，它们只可能会被分别加入匹配区间和删除一次，因此时间是线性的。

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
char s[N];
int z[N];
int main(){
	scanf("%s",s+1);
	int n=strlen(s+1);
	int r=0;
	z[1]=0;
	printf("0 ");
	for(int i=2;i<=n;i++){
		while(s[r+1]!=s[i]&&r)
			r=z[r];
		if(s[r+1]==s[i])r++;
		z[i]=r;
		printf("%d ",z[i]);
	}
	return 0;
}

P3426 [POI 2005] SZA-Template

很好的一题，最初的想法是对于每个 \(S[:i]\) 都跑一遍 DP，利用 \(\texttt{Fail}\) 树看看能否将一个完整的串表示出来，后来发现这完全就是多此一举。不需要钦定一个长度 \(i\)，直接 DP 即可。

具体来说，对于每一个串我们考虑如何完全覆盖它的答案形态。令 \(f_i\) 表示 \(S[:i]\) 的最小覆盖长度，注意到对于每个 \(i\) 这是唯一的，而且只可能随着 \(i\) 的增大单调不减。然后处理 \(f_i\) 的时候，我们要找到一个 \(j\in [i-z[i],i-1]\)，使得 \(f_j=f_{z[i]}\)，后面剩余的必然可以通过和覆盖 \(f_{z[i]}\) 一样的方法覆盖，那么此时 \(f_i=f_{z[i]}\)，否则 \(f_i=i\)。

代码实现上，你可以对于每个 \(f_i\) 记录一个最大 \(i\) 的值然后判断，转移即可。当然你也可以把这个桶搞成动态的，桶内只记录匹配区间 \([i-z[i],i-1]\) 的值存在的个数，但是这样的做法非常难调而且调了半天调出 5 种分数愣是不知道错哪儿，所以建议使用第一种 😦。

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
int n,z[N],buk[N],f[N];
char s[N];
int main(){
	scanf("%s",s+1);
	n=strlen(s+1);
	int r=0;
	for(int i=2;i<=n;i++){
		while(r&&s[r+1]!=s[i])
			r=z[r];
		if(s[r+1]==s[i])r++;
		z[i]=r;
	}
	buk[f[1]=1]=1;
	for(int i=2;i<=n;i++){
		f[i]=i;
		if(buk[f[z[i]]]>=i-z[i])f[i]=f[z[i]];
		buk[f[i]]=i;
	}
	printf("%d",f[n]);
	return 0;
}

扩展 KMP

跟 \(\text{Border}\) 没什么关系。巧妙利用匹配性质最大化利用重复段，减小时间耗费。这里没有图但是显然为了理解该算法，不画图是不可能的，读者应根据描述画出相应图像辅助理解，至于为什么不画图完全是因为太懒了。

P5410 【模板】扩展 KMP/exKMP（Z 函数）

Problem：求数组 \(z\)，\(z[i]\) 是最大的 \(S[:z[i]]=S[n-z[i]+1:]\) 的值。

考虑顺序求解，记录右端点最大化的匹配 \([l,r]\)（不包括 \([1,n]\)），考虑求解 \(z[i]\)，必有 \(l<i\)，分类讨论。

当 \(r<i\)，将 \(z[i]\) 清零并暴力扩展。
当 \(r\geq i\)，可以省去 \([i,r]\) 的匹配。具体来说，一定有 \(S[i:r]=S[i-l+1:r-l+1]\)，那么对于这个匹配的快速求解只需要取到 \(z[i-l+1]\) 即可，即 \(z[i]=\min(i-r+1,z[i-l+1])\)，然后继续暴力扩展。

Problem：求数组 \(q\)，\(q[i]\) 是最大的 \(S[:q[i]]=T[i:i+q[i]-1]\) 的值。

考虑利用求过的 \(z\) 数组。同样地，记录在 \(T\) 上右端点最大化的匹配 \([l,r]\)，则定有 \(T[l:r]=S[1:r-l+1]\)，和上面一样的分类讨论，如果 \(r<i\) 那么清零并暴力扩展。如果 \(r\geq i\) 那就一定有 \(T[i:r]=S[i-l+1:r-l+1]\)，取到 \(z[i-l+1]\) 即可省略 \([l,r]\) 的匹配，然后暴力扩展。

注意到在以上两个问题的情景中，\(r\) 都是单调不减的，所以总的时间复杂度都是线性的。

代码实现：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=2e7+5;
char s[N],t[N];
int n,m,z[N],q[N];
int main(){
	scanf("%s",t+1);m=strlen(t+1);
	scanf("%s",s+1);n=strlen(s+1);
	int l=-1,r=-1;
	z[1]=n;
	for(int i=2;i<=n;i++){
		if(i<=r)z[i]=min(r-i+1,z[i-l+1]);
		while(i+z[i]<=n&&s[i+z[i]]==s[1+z[i]])z[i]++;
		if(i+z[i]-1>r)l=i,r=i+z[i]-1;
	}
	l=-1,r=-1;
	for(int i=1;i<=m;i++){
		if(i<=r)q[i]=min(r-i+1,z[i-l+1]);
		while(i+q[i]<=m&&1+q[i]<=n&&s[1+q[i]]==t[i+q[i]])q[i]++;
		if(i+q[i]-1>r)l=i,r=i+q[i]-1;
	}
	LL pans=0;
	for(int i=1;i<=n;i++)
		pans^=1ll*i*(z[i]+1);
	printf("%lld\n",pans);
	pans=0;
	for(int i=1;i<=m;i++)
		pans^=1ll*i*(q[i]+1);
	printf("%lld",pans);
	return 0;
}

\(\texttt{Fail}\) 树

KMP

其实就是把 \(\text{Bd}\) 具象化了，将每一个 \(\text{Bd}\) 的匹配视为一条边，就可以建成一棵树。利用这棵树可以解决一些问题包括但不限于：

对于每个前缀首尾不重合的 \(\text{Bd}\) 数量（P2375 [NOI2014] 动物园）。
对于任意两个不同前缀的最长公共 \(\text{Bd}\) 数量（P5829 【模板】失配树）。

应用较为简单，只放代码不做讲解。

//P2375
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MOD=1e9+7;
const int N=1e6+5;
char s[N];
int z[N],num[N];
vector<int>G[N];
int stk[N],tp;
void dfs(int u){
	num[u]=num[stk[tp]];
	stk[++tp]=u;
	while(num[u]+1<tp&&stk[num[u]+1]*2<=u)num[u]++;
	for(int v:G[u])
		dfs(v);
	num[u]--;
	stk[tp--]=0;
}
int main(){
	int T=0;
	scanf("%d",&T);
	while(T--){
		scanf("%s",s+1);
		int n=strlen(s+1);
		for(int i=0;i<=n;i++)
			G[i].clear();
		int r=0;
		z[1]=0;
		G[0].push_back(1);
		for(int i=2;i<=n;i++){
			while(s[r+1]!=s[i]&&r)
				r=z[r];
			if(s[r+1]==s[i])r++;
			z[i]=r;
			G[r].push_back(i);
		}
		dfs(0);
		LL pans=1;
		for(int i=1;i<=n;i++)
			pans=pans*(num[i]+1)%MOD;
		printf("%lld\n",pans);
	}
	return 0;
}

AC 自动机

和 KMP 不同的地方是，\(\texttt{Fail}\) 指针在字典树上转移，并且可能由一个模式串转移到另一个上，不再是只能从自己转移到自己。把所有 \(\texttt{Fail}\) 指针拎出来可建成一棵新树称为 AC 自动机的 \(\texttt{Fail}\) 树。

接下来我们将介绍 AC 自动机。

AC 自动机

解决问题：多个模式串 \(T_i\) 与文本串 \(S\) 的快速匹配问题。

时间/空间复杂度均为 \(O(n|\Sigma|)\)，\(n\) 为字典树节点个数，\(\Sigma\) 为字母表。

KMP 可以做到在 \(O(n+m)\) 的时间内完成一对一的匹配，如果我们改成多对一呢？

学习 KMP 的思想，我们可以把每一个模式串 \(T_i\) 都放进一棵字典树中，我们考虑利用 \(\texttt{Fail}\) 指针表示 \(\text{mxBd}\)，不同的地方在于不再像 KMP 那样只有一个模式串（这个时候 \(\texttt{Fail}\) 指针只会由自己指向自己的前缀），而是有多个，所以 \(\texttt{Fail}\) 还可以指到其他模式串的前缀上，毕竟我们最终要匹配所有模式串。可以证明从一个点不断往上跳 \(\texttt{Fail}\) 指针包含了所有模式串 \(\text{Bd}\) 的情况，因为每个 \(\texttt{Fail}\) 指针代表的都是 \(\text{mxBd}\)，不会跳过任何一个 \(\text{Bd}\)。

接下来，我们定义一个节点 \(u\) 的 \(\texttt{Fail}\) 链表示它沿着 \(\texttt{Fail}\) 指针向上一直跳到根节点所构成的链。

如何求出 \(\texttt{Fail}\) 指针？字典树上 BFS 即可。根据 KMP 的思路，对于一个节点 \(u\)，它相当于在父亲 \(fa\) 的基础上增加了一个字符，可以针对 \(fa\) 维护一个指针，如果失配就往上跳直到找到 \(\texttt{Fail}\) 链上有一个点存在新增字符的那个儿子。

这样做在 KMP 来是容易的，但是在树形结构上比较困难。那么我们考虑偷个懒，对于每个节点 \(fa\) 到 \(26\) 个儿子直接转移，如果该儿子存在那么它的 \(\texttt{Fail}\) 就是 \(fa\) 的 \(\texttt{Fail}\) 的对应儿子节点（不存在就是没有），如果该儿子不存在那么就将该儿子置为它的 \(\texttt{Fail}\) 的对应儿子节点。这样就保证了访问过的节点 \(fa\) 的所有 \(26\) 个儿子一定包含它的 \(\texttt{Fail}\) 链上的最深存在儿子。

注意：某些题目中这个懒不能乱偷，如果后续要用到这棵 Trie 做 DFS 之类的操作且不能经过 \(\texttt{Fail}\) 边，那么我们需要给每个新加的儿子节点都打上一个 \(\texttt{tag}\)，在 DFS 的时候如果有这个 \(\texttt{tag}\) 就不走这条边，防止无限递归与重复计算。

应用是简单的，以模板为例，我们需要求取每个模式串在文本串中的出现次数。匹配每个 \(S\) 的前缀只需要在树上跳 \(\texttt{Fail}\) 指针即可，然后匹配的其实是当前所在节点的 \(\text{Fail}\) 链上面所有存在的完整串（在末尾打标记）。这个东西不是很好求，其实换个角度就相当于单点加，然后每个打了标记的节点 \(u\) 的子树中求加了多少个点，可以直接建出 \(\texttt{Fail}\) 树（当然不实际建出也可以），然后在 \(\texttt{Fail}\) 树上 DFS 做树上差分即可。

如果不想建出 \(\texttt{Fail}\) 树，由于这是一棵内向树，那么也可以用一个拓扑处理，效果是一样的。值得一提的是，该题的题解中很多都提到了拓扑优化，但是都没有提及其本质 \(\texttt{Fail}\) 树的子树统计。

P5357 【模板】AC 自动机

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
struct Node{
	int son[26],end,fail,ans;
}t[N];
int in[N];
int cnt,an[N];
void ins(string s,int num){
	int now=0;
	for(int i=0;i<s.size();i++){
		int ch=s[i]-'a';
		if(t[now].son[ch]==0)
			t[now].son[ch]=cnt++;
		now=t[now].son[ch];
	}
	t[now].end=num;
}
void gtf(){
	queue<int>q;
	for(int i=0;i<26;i++)
		if(t[0].son[i])
			q.push(t[0].son[i]);
	while(!q.empty()){
		int now=q.front();
		q.pop();
		for(int i=0;i<26;i++){
			if(t[now].son[i]){
				t[t[now].son[i]].fail=t[t[now].fail].son[i];
				in[t[t[now].son[i]].fail]++;
				q.push(t[now].son[i]);
			}
			else t[now].son[i]=t[t[now].fail].son[i];
		}
	}
}
void query(string s){
	int now=0;
	for(int i=0;i<s.size();i++)
		now=t[now].son[s[i]-'a'],t[now].ans++;
}
void topu(){
	queue<int>q;
	for(int i=1;i<=cnt;i++)
		if(in[i]==0)q.push(i);
	while(!q.empty()){
		int now=q.front();q.pop();an[t[now].end]=t[now].ans;
		int v=t[now].fail;in[v]--;
		t[v].ans+=t[now].ans;
		if(in[v]==0)q.push(v);
	}
}
map<string,int>mp;
string s[N];
string str;
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cnt=1;
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){cin>>s[i];ins(s[i],i);mp[s[i]]=i;}
	gtf();
	cin>>str;
	query(str);
	topu();
	for(int i=1;i<=n;i++){
		cout<<an[mp[s[i]]]<<'\n';
	}
	return 0;
}

CF710F String Set Queries

观察到难点主要在于 AC 自动机要求进行完所有插入后统一重构一次，这个重构是 \(O(n)\) 的，然后才能统一计算答案，因此 AC 自动机不支持动态加入动态查询。考虑优化重构过程，采用二进制分组。具体来说，开 \(O(\log n)\) 个 AC 自动机，最新的 AC 自动机开在最末尾，每当末尾有两个相同大小的 AC 自动机就合并，暴力重构。这样开出来的实时数量是 \(O(\log n)\) 的，每次查询直接查 \(\log n\) 个 AC 自动机即可。同时根据观察，每个点最多会被合并 \(\log n\) 次，于是总时间复杂度 \(O(n\log n)\)。

点击查看代码

#pragma GCC optimize(2)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
const int N=3e5+5;
int m;
string s;
struct AC{
	struct Node{int ch[26],fail,cnt;}t[N];
	int ncnt,ocnt[N],q[N],hd,tl;
	int rt[N],cntr,L[N],R[N];
	int stk[N],tp;
	string sm[N];
	inline void init(int u){t[u]=t[0];}
	void ins(int &root){
		if(!root)init(root=++ncnt);
		int now=root;
		for(int i=0;i<s.size();i++){
			int go=s[i]-'a';
			if(!t[now].ch[go])
				init(t[now].ch[go]=++ncnt);
			now=t[now].ch[go];
		}
		t[now].cnt++;
	}
	void build(int root){
		hd=1;tl=0;
		ocnt[root]=0;
		t[root].fail=root;
		for(int i=0;i<26;i++){
			if(t[root].ch[i])q[++tl]=t[root].ch[i];
			else t[root].ch[i]=root;
		}
		while(hd<=tl){
			int u=q[hd++];
			if(!t[u].fail)t[u].fail=root;
			ocnt[u]=t[u].cnt+ocnt[t[u].fail];
			for(int i=0;i<26;i++){
				if(!t[u].ch[i])t[u].ch[i]=t[t[u].fail].ch[i];
				else t[t[u].ch[i]].fail=t[t[u].fail].ch[i],q[++tl]=t[u].ch[i];
			}
		}
	}
	void merge(int rt1,int rt2){
		ncnt=rt[rt1]-1;
		L[rt2]=L[rt1];
		rt[rt1]=rt[rt2]=0;
		for(int i=L[rt2];i<=R[rt2];i++)
			s=sm[i],ins(rt[rt2]);
		build(rt[rt2]);
	}
	void Insert(){
		sm[++cntr]=s;
		L[cntr]=R[cntr]=cntr;
		ins(rt[cntr]);build(rt[cntr]);
		while(tp&&R[cntr]-L[cntr]+1==R[stk[tp]]-L[stk[tp]]+1)
			merge(stk[tp--],cntr);
		stk[++tp]=cntr;
	}
	LL que(){
		LL res=0;
		for(int id=1;id<=tp;id++){
			int now=rt[stk[id]];
			for(int i=0;i<s.size();i++){
				int go=s[i]-'a';
				now=t[now].ch[go];
				res+=ocnt[now];
			}
		}
		return res;
	}
}T1,T2;
int main(){
	cin>>m;fflush(stdout);
	for(int i=1;i<=m;i++){
		int op;
		cin>>op>>s;
		if(op==1)T1.Insert();
		else if(op==2)T2.Insert();
		else cout<<T1.que()-T2.que()<<'\n';
		fflush(stdout);
	}
	return 0;
}

回文串

Manacher

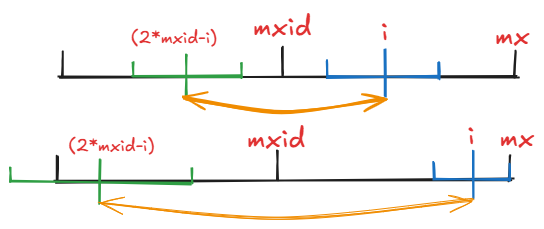
欸大概是这么个东西吧。

考虑到回文串长度可能是偶数，在每两个字符之间加入一个特殊字符 #，如果是偶数可以以其为回文中心扩展，每次从 \(0\) 开始暴力扩展是 \(O(n^2)\) 的，即每次判断左右是否有相等字符。考虑已经扩展 \([1,i-1]\) 这么多个回文中心，其中之前扩展最大右边界为 \(mx\)，其对应回文中心为 \(mxid\)。考虑如何迅速转移出 \(P[i]\)（以 \(i\) 为回文中心最多能单向扩展多少个字符）。

显然不能再从 \(0\) 开始。发现可以利用先前处理的信息，如果 \(i\le mx\)，可以根据上图快速把 \(P[i]\) 推到边界 \(mx\) 上，然后再在 \(mx\) 上开始继续扩展。根据这样的理论，每次扩展右边界都不小于先前。如果是上图的情况就无法扩展。于是可以做到 \(O(n)\)。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=1.1e7+5;
char rS[N];
char S[N<<1];
int P[N<<1],n;
void init(){
	n=strlen(rS);
	int k=0;
	S[k++]='$';S[k++]='#';
	for(int i=0;i<n;i++){
		S[k++]=rS[i];
		S[k++]='#';
	}
	S[k++]='&';
	n=k;
}
int manacher(){
	int ans=1,mx=0,mxid=0;
	for(int i=1;i<n;i++){
		if(i<mx)P[i]=min(mx-i,P[2*mxid-i]);
		else P[i]=1;
		while(S[i+P[i]]==S[i-P[i]])P[i]++;
		if(P[i]+i>mx)mx=P[i]+i,mxid=i;
		ans=max(ans,P[i]);
	}
	return ans-1;
}
signed main(){
	scanf("%s",rS);
	init();
	printf("%d",manacher());
	return 0;
}

回文自动机（PAM）

PAM 的意义

PAM 是一棵双向扩展的 trie。

每次加入 \(S[n]=c\) 相当于产生若干以 \(c\) 为结尾的新回文串。我们让这里的 \(\texttt{Fail}\) 指针指向回文子串的位置，那么建出 trie 后只需要沿着 \(\texttt{Fail}\) 链向上跳就可以找到所有回文子串。建出这个东西以后对于字符串的每个前缀/后缀都可以找到一个对应的节点，以前缀为例，其代表的是等效的 \([1,i]\) 的最长回文后缀。

通过这个 DFA 我们可以很方便地计算每个以 \(i\) 为结尾/起点的回文串数量/最长回文串长度，相比于原来 Manacher 只能从中间统计在部分应用场景下有不小的优势。

构建过程

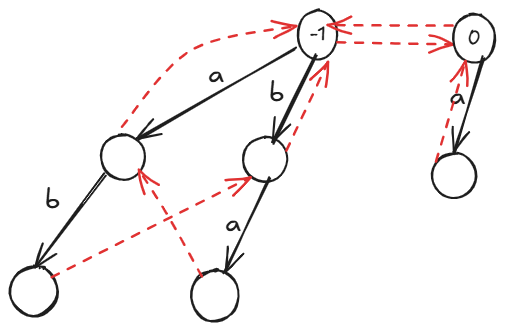
（以上是以串 \(aabab\) 建出的回文自动机）

如何建出这个 PAM？考虑增量法构造，\(i\to i+1\) 的转移，找到 \(i\) 对应节点 \(last\)，其长度即为 \(len[last]\)，只需找到 \(\texttt{Fail}\) 链上第一个满足原串上其最后一个个不包含的字符 \(=\) 新加入的字符 \(c\)，这样就可以前后同时扩展。这样就可以每次前后拓展一位，找到其 \(father\)。对于其 \(\texttt{Fail}\) 的计算，直接暴力跳即可。跳 \(\texttt{Fail}\) 的过程实际上均摊下来是 \(\Theta(n)\) 的。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=5e5+5,S=26;
int n,ans;
char s[N];
namespace PAM{
	int n,len[N],cnt[N],fail[N],ch[N][S],las,tot,s[N];
	void init(){s[0]=-1;len[1]=-1,len[n=0]=0;fail[0]=1;las=tot=1;}
	inline int getfail(int x){
		while(s[n]!=s[n-1-len[x]])
			x=fail[x];
		return x;
	}
	int add(int c){
		s[++n]=c;
		int p=getfail(las);
		if(!ch[p][c]){
			fail[++tot]=ch[getfail(fail[p])][c];
			ch[p][c]=tot;
			cnt[tot]=cnt[fail[tot]]+1;
			len[tot]=len[p]+2;
		}
		return cnt[las=ch[p][c]];
	}
}
int main(){
	//freopen("pam.in","r",stdin);
	//freopen("pam.out","w",stdout);
	scanf("%s",s+1);n=strlen(s+1);
	PAM::init();
	for(int i=1;i<=n;i++)
		printf("%d ",ans=PAM::add((s[i]-97+ans)%26));
	return 0;
}

posted @ 2025-07-07 16:41 TBSF_0207 阅读(20) 评论(0) 收藏举报

刷新页面返回顶部

TBSF-0207

给岁月以文明，给时光以生命 | cnblogs.com/TBSF-0207

（笔记）DFA 简介字符串相关 Border KMP AC 自动机 Manacher 回文自动机 PAM

DFA 确定性有限状态自动机

Border

KMP

P3426 [POI 2005] SZA-Template

扩展 KMP

\(\texttt{Fail}\) 树

KMP

AC 自动机

AC 自动机

CF710F String Set Queries

回文串

Manacher

回文自动机（PAM）

PAM 的意义

构建过程

公告

TBSF-0207

给岁月以文明，给时光以生命 | cnblogs.com/TBSF-0207

（笔记）DFA 简介 字符串相关 Border KMP AC 自动机 Manacher 回文自动机 PAM

DFA 确定性有限状态自动机

Border

KMP

P3426 [POI 2005] SZA-Template

扩展 KMP

\(\texttt{Fail}\) 树

KMP

AC 自动机

AC 自动机

CF710F String Set Queries

回文串

Manacher

回文自动机（PAM）

PAM 的意义

构建过程

公告

（笔记）DFA 简介字符串相关 Border KMP AC 自动机 Manacher 回文自动机 PAM