（笔记）树的直径

好远古的东西，但是一点都不会。

树的直径

定义

树上任意两点最长距离称为树的直径。
直径的中点定义为其严格中点，即路径 \(u\rightarrow v\) 上存在一中点 \(x\)，使得 \(dis_{u,x}=dis_{x,v}\)，该点也可以在边上。

性质

Lemma0：所有直径都相交。

Proof：

假设存在两条不相交的直径 \(u\rightarrow v,x\rightarrow y\)。在联通树种必然存在这样一条路径 \(P\)，在 \(P\) 上可以取到 \(p\in u\rightarrow v,q\in x\rightarrow y\)。通过拼接后，可能出现更长路径 \(\max\{dis_{u,x},dis_{u,y},dis_{v,x},dis_{v,y}\}\)，故与原假设矛盾，命题成立。

Lemma1：所有直径都至少经过一点，且该点一定是直径中点。

Proof：我们考虑反证法：

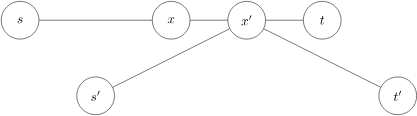
（摘自 OI-wiki）

显然对于上图两条直径 \(s\rightarrow t,s'\rightarrow t'\)，有 \(dis_{s,x}=dis_{x,t}=dis_{s',x'}=dis_{x',t'}\)。假设 \(x\neq x'\)，此时必然能够找到 \(dis_{s,t'}=dis_{s,x'}+dis_{x',t'}>dis_{s,t'}+dis_{x',t}=dis_{s,t}\)，与 \(s\rightarrow t\) 为直径矛盾。

Lemma2：对于一棵树内的节点 \(u\)，\(v\) 是距离 \(u\) 最远的一个节点，那么 \(v\) 一定是树上直径的一个端点。

Proof：考虑一条直径 \(A\rightarrow B\)。

分类讨论：

如果 \(u\) 在 \(A\rightarrow B\) 上，那么它可以把直径劈成两半。可以证明如果把 \(u\) 提为树根，那么两半必定一个是最长链，一个是次长链（以 \(u\) 为链的一端）。如果不是，那么必然可以对于任意一半找到一个更长的代替，那么直径也就不是原来的 \(A\rightarrow B\) 了。因为有最长链，所以 \(A\) 或 \(B\) 一定有一个就是结论中的 \(v\)。
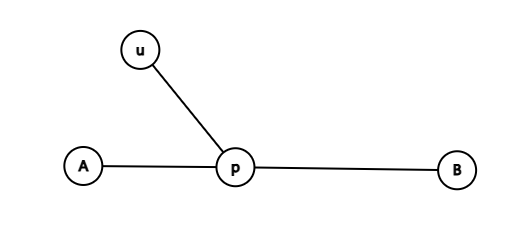
如果 \(u\) 不在 \(A\rightarrow B\) 上，它一定可以通过一个点 \(p\) 接到 \(A\rightarrow B\) 上，由上，\(dis_{u,p}\le dis_{A,p}\)，\(dis_{u,p}\le dis_{B,p}\)。

考虑到 \(u\) 外面可能还接着一些节点如 \(fa\)，那么 \(dis_{u,fa}+dis_{u,p}\le\) 最长链长度，\(dis_{u,fa}\le\) 最长链长度 \(-dis_{u,p}<\) 最长链长度 \(+dis_{u,p}\)。

考虑 \(fa\) 接在 \(u\rightarrow p\) 上的情况，如果 \(dis_{u,fa}>max(dis_{u,A},dis_{u,B})\)，那么一定可以找到比 \(A\rightarrow B\) 更长的直径。

那么 \(v\) 一定接在 \(A\rightarrow B\) 异于 \(p\) 的 \(u\) 方向子树上了。换句话说，就是 \(u\rightarrow v\) 这条路径必然包含 \(u\rightarrow p\)。容易知道，最长路径一定是 \(dis_{u,p}+max(dis_{A,p},dis_{B,p})\) 了。

Lemma3：将一棵树通过直径上的一条边分割成两棵树。对于被分割的树，它的直径一端一定是未被分割的树直径的一端。

Proof：

（摘自题解 P3761 【[TJOI2017]城市】）

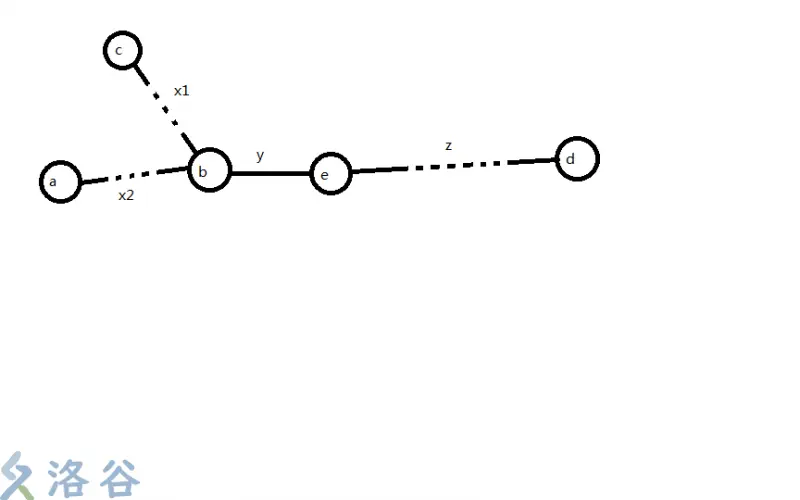
\(a\rightarrow d\) 为原树直径，\(c\rightarrow a\) 为新直径，要删掉边 \(b\rightarrow e\)。根据直径的定义，显然 \(x_1>x_2\) 的点 \(c\) 是不存在的，否则原树直径就会变成 \(c\rightarrow d\)。即对于一棵被分割出来的树，\(a\) 是距离 \(b\) 最远的节点，根据 Lemma2 可以知道 \(a\) 是直径的一个端点。

Lemma4：两棵树相连，新直径的两端点一定是原四个端点中的两个。

Lemma5：一棵树上接一个叶子节点，直径最多改变一个端点。

求法

直径

两次 DFS

利用 Lemma2，先找出任意一个节点的距离最远节点记为 \(rt\)，然后以 \(rt\) 为根求出最远点记为 \(ed\)，则 \(rt\rightarrow ed\) 就是一条直径。

需要注意的是，这种方法有一定局限性，不能处理负权边，而且只能找到一条直径。

void dfs0(int u,int fa){
	dep[u]=dep[fa]+1;
	if(dep[u]>dep[st])st=u;
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].v,w=e[u].w;
		if(v==fa)continue;
		dfs0(v,u);
	}
}
void dfs1(int u,int fa){
	dep[u]=dep[fa]+1;
	if(dep[u]>dep[ed])ed=u;
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].v,w=e[u].w;
		if(v==fa)continue;
		dfs1(v,u);
	}
}

树形 DP

实质是对每一个点的子树记一个 \(mxdep_u\) 和 \(cdep_u\) 分别代表子树内最长和次长链长度，分别转移然后直径长度就是 \(\max_i (mxdep_i+cdep_i)\)。

更好的方法当然是只记录 \(mxdep_u\)，然后每次直接拿 \(dis_v+w+mxdep_u\) 更新直径长度，但是鉴于有些时候次长链还是挺有用的遂保留。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e4+5,INF=1e9;
int n,head[N],idx;
struct Edge{int v,next,w;}e[N<<1];
void ins(int x,int y,int z){
	e[++idx].v=y;
	e[idx].next=head[x];
	e[idx].w=z;
	head[x]=idx;
}
int dis[N],mxdep[N],cdep[N];
int ans;
void dfs(int u,int fa){
	cdep[u]=-INF;
	mxdep[u]=dis[u];
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].v,w=e[i].w;
		if(v==fa)continue;
		dis[v]=dis[u]+w;
		dfs(v,u);
		if(mxdep[v]>mxdep[u])cdep[u]=mxdep[u],mxdep[u]=mxdep[v];
		else if(mxdep[v]>cdep[u])cdep[u]=mxdep[v];
	}
	if(cdep[u]!=-INF)
		ans=max(1ll*ans,1ll*mxdep[u]+cdep[u]-dis[u]*2);
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<n;i++){
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		ins(u,v,w);
		ins(v,u,w);
	}
	dfs(1,0);
	printf("%d",ans);
	return 0;
}

直径中点（交点）

三次 DFS。根据暴力解法，我们可以先用两次 DFS 找出一条直径，然后再在这条直径里面找中点。

void dfs(int u,int fa){
	if(dep[u]>dep[rt])rt=u;
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].v,w=e[i].w;
		if(v==fa)continue;
		dep[v]=dep[u]+w;
		dfs(v,u);
	}
}
void dfsn(int u,int fa){
	if(dep[u]>dep[ed])ed=u;
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].v,w=e[i].w;
		if(v==fa)continue;
		dep[v]=dep[u]+w;
		dfsn(v,u);
	}
}
bool dfsm(int u,int fa){
	bool my=0;
	if(u==ed)return 1;
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].v,w=e[i].w;
		if(v==fa)continue;
		my|=dfsm(v,u);
	}
	if(my&&dep[u]>=dep[ed]/2)rt=u;
	return my;
}

但是这个东西写起来简直宛如吃史，所以当然有更好的方法。

直接 DP。

void dfs(int u,int fa){
	mxd[u]=cd[u]=0;
	for(int v:G[u]){
		if(v==fa)continue;
		dfs(v,u);
		if(mxd[v]+1>mxd[u])cd[u]=mxd[u],mxd[u]=mxd[v]+1;
		else if(mxd[v]+1>cd[u])cd[u]=mxd[v]+1;
	}
	if(mxd[u]+cd[u]>D)rt=u,D=mxd[u]+cd[u];
}

这个东西求出的不一定是直径中点，但是一定是直径交点。为什么呢？这个求法来自「DROI」Round 1 距离题解，这里给出一个粗略的证明。

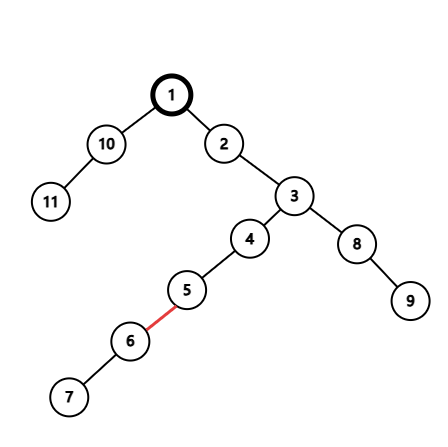
Lemma4：对于最深的满足 \(mxdep_u+cdep_u=D\) 的节点，它一定在所有直径交集上。

Proof：假如我们在节点 \(u=1\) 找到了一个最大的 \(mxdep_u+cdep_u=D\)，它在直径 \(A\rightarrow B\) 上，深度最大化（本例中，\(A=11,B=9\)），且让 \(A\) 为深度较小的一端。（那么有 \(cdep_u=dis_{u,A},mxdep_u=dis_{u,B}\)）

考虑构造一个东西使命题非法，显然 \(A\rightarrow B\) 已经是一条直径，根据 Lemma0，所有直径相交，我们需要做的就是找到直径上一点 \(v\)，构造一分叉使得其与直径不包含 \(u\) 的一边构成一条直径，它需要与 \(A\rightarrow B\) 等长。

显然这个东西不可能直接接在 \(u\) 上，否则构造出来的新直径分叉一定会经过点 \(u\)，相当于没有构造。

如果接在 \(A\rightarrow u\) 上，需要在 \(v\) 下方接一条长度为 \(dis_{v,B}\) 的链，显然这条链的长度会使得 \(cdep_u\) 变大，构造不合法。

再考虑在 \(u\rightarrow B\) 上接一条链，要满足长度为 \(2dis_{A,v}\le dis_{A,B}\)（否则就会构成更长的直径）。这时候就一定可以在 \(v\) 上面找到 \(mxdep_v+cdep_v=D\)，而且 \(v\) 深度更深，与 \(u\) 的定义矛盾。

综上所述，命题成立。

例题

P3629 [APIO2010] 巡逻

好久以前真的一点也不会呢，丢了一年多才捡起来，然后发现当时的自己是 rz。

具体来说，采用反悔贪心思想。对于 \(K=2\)，我们需要选两条路径，把它们的首尾连边形成环，那么手搓一下题意就可以得到如下结论：如果两环没有重合，\(ans\) 直接减少路径长度然后 \(+2\)。否则重合的部分仍然需要走两次。这时就需要用到负权边处理了。

先通过两次 DFS 找出一条直径，新建一条道路，记下答案，即为 \(K=1\) 时的答案。对于 \(K=2\)，把找出的直径上的所有边都变为负权边，边权为 \(-1\)，给程序一个反悔的机会。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,INF=1e9;
int n,k,idx,head[N],fat[N],ans;
struct Edge{int v,next,w;}e[N<<1];
void ins(int x,int y,int z){
	e[++idx].v=y;
	e[idx].next=head[x];
	e[idx].w=z;
	head[x]=idx;
}
int st,ed,dep[N];
void dfs0(int u,int fa){
	dep[u]=dep[fa]+1;
	if(dep[u]>dep[st])st=u;
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].v,w=e[i].w;
		if(v==fa)continue;
		dfs0(v,u);
	}
}
void dfs1(int u,int fa){
	dep[u]=dep[fa]+1;
	fat[u]=fa;
	if(dep[u]>dep[ed])ed=u;
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].v,w=e[i].w;
		if(v==fa)continue;
		dfs1(v,u);
	}
}
int mxdep[N],cdep[N],D;
void upd(int u,int w){
	if(w>mxdep[u])cdep[u]=mxdep[u],mxdep[u]=w;
	else if(w>cdep[u])cdep[u]=w;
}
void dfs2(int u,int fa){
	mxdep[u]=0;
	cdep[u]=-INF;
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].v,w=e[i].w;
		if(v==fa)continue;
		dfs2(v,u);
		upd(u,mxdep[v]+w);
	}
	if(cdep[u]!=-INF)
		D=max(D,mxdep[u]+cdep[u]);
}
int main(){
	scanf("%d%d",&n,&k);ans=2*(n-1);
	for(int i=1;i<n;i++){
		int u,v;
		scanf("%d%d",&u,&v);
		ins(u,v,1);ins(v,u,1);
	}
	dfs0(1,0);
	dep[0]=-1;
	dfs1(st,0);
	ans-=dep[ed]-1;
	if(k==1){
		printf("%d",ans);
		return 0;
	}
	for(int u=ed,lst=0;u;lst=u,u=fat[u]){
		for(int j=head[u];j;j=e[j].next){
			int v=e[j].v;
			if(v==fat[u])e[j].w=-1;
			if(v==lst)e[j].w=-1;
		}
	}
	dfs2(1,0);
	ans-=D-1;
	printf("%d",ans);
	return 0;
}

P8981 「DROI」Round 1 距离

模拟赛 \(T_1\)，被自己糖飞。结论记错了，以为所有直径都经过重心，获得了 5pts 的好成绩！

场上的写法很神秘，分讨思想是对的，先把直径中点拉上来提为根，然后再 DFS 计数。场上混淆了很多东西，包括但不限于最长链和次长链需要在不同儿子上，计算最长链和次长链要分开（当然如果按照一般方法两条链长度相等说明最长链 \(cnt>1\)）。

如果有多条最长链，那么所有直径就是所有最长链两两匹配的结果，否则就是一条最长链与所有次长链匹配的结果，两者都容易用树上差分直接路径加处理。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MOD=998244353;
const int N=5e6+5,INF=1e9;
int n,k,siz[N],rt;
vector<int>G[N];
int mxd[N],cd[N];
vector<int>mx,c,dmx,dc;
int D,cnt[N];
void dfs(int u,int fa){
	mxd[u]=cd[u]=0;
	for(int v:G[u]){
		if(v==fa)continue;
		dfs(v,u);
		if(mxd[v]+1>mxd[u])cd[u]=mxd[u],mxd[u]=mxd[v]+1;
		else if(mxd[v]+1>cd[u])cd[u]=mxd[v]+1;
	}
	if(mxd[u]+cd[u]>D)rt=u,D=mxd[u]+cd[u];
}
void dfs1(int u,int fa){
	mxd[u]=0;cnt[u]=1;
	for(int v:G[u]){
		if(v==fa)continue;
		dfs1(v,u);
		if(mxd[v]+1>mxd[u])mxd[u]=mxd[v]+1,cnt[u]=cnt[v];
		else if(mxd[v]+1==mxd[u])
			cnt[u]+=cnt[v];
	}
}
LL cf[N],ans;
void dfsp(int u,int fa,int val){
	bool leaf=1;
	for(int v:G[u]){
		if(v==fa)continue;
		if(mxd[v]+1!=mxd[u])continue;
		leaf=0;
		dfsp(v,u,val);
		cf[u]=(cf[u]+cf[v])%MOD;
	}
	if(leaf)cf[u]=val;
}
int main(){
	scanf("%d%d",&n,&k);
	if(n==1){
		printf("1");
		return 0;
	}
	for(int i=1;i<n;i++){
		int u,v;
		scanf("%d%d",&u,&v);
		G[u].push_back(v);
		G[v].push_back(u);
	}
	dfs(1,0);
	dfs1(rt,0);
	int son1=0,son2=0;
	int d1=-1,d2=-1;
	int num1=0,num2=0;
	for(int v:G[rt]){
		if(mxd[v]>d1)d1=mxd[v],son1=1,num1=cnt[v];
		else if(mxd[v]==d1)son1++,num1+=cnt[v];
	}
	for(int v:G[rt]){
		if(mxd[v]==d1)continue;
		if(mxd[v]>d2)d2=mxd[v],son2=1,num2=cnt[v];
		else if(mxd[v]==d2)son2++,num2+=cnt[v];
	}
	if(son1==1){
		if(!son2){
			for(int v:G[rt]){
				if(mxd[v]==d1)
					dfsp(v,rt,1);
				cf[rt]=(cf[rt]+cf[v])%MOD;
			}
		}
		else {
			for(int v:G[rt]){
				if(mxd[v]==d1)
					dfsp(v,rt,num2);
				else if(mxd[v]==d2)
					dfsp(v,rt,num1);
				cf[rt]=(cf[rt]+cf[v])%MOD;
			}
		}
	}
	else {
		for(int v:G[rt]){
			if(mxd[v]==d1)
				dfsp(v,rt,num1-cnt[v]);
			cf[rt]=(cf[rt]+cf[v])%MOD;
		}
	}
	if(son1+son2>=2){
		if(cf[rt]&1)cf[rt]=(cf[rt]+998244353)/2%MOD;
		else cf[rt]=cf[rt]/2%MOD;
	}
	for(int i=1;i<=n;i++){
		if(k==2)ans=(ans+cf[i]*cf[i]%MOD)%MOD;
		else ans=(ans+cf[i])%MOD;
	}
	printf("%lld",ans);
	return 0;
}

posted @ 2025-05-29 18:15 TBSF_0207 阅读(39) 评论(0) 收藏举报

刷新页面返回顶部

TBSF-0207

给岁月以文明，给时光以生命 | cnblogs.com/TBSF-0207

（笔记）树的直径

树的直径

定义

性质

求法

直径

直径中点（交点）

例题

P3629 [APIO2010] 巡逻

P8981 「DROI」Round 1 距离

公告